带定性判断的计分投票制及其公理刻画

赵伟

1 Introduction

Self-organization is a process where a stable pattern is formed by the cooperative behavior between parts of an initially disordered system without external control or influence.It has been introduced to multi-agent systems as an internal control process or mechanism to solve difficult problems spontaneously,especially if the system is operated in an open environment thereby having no perfect and a priori design to be guaranteed.([8,9,10])When the system is deployed in an open environment,agents can enter or exit the system.It might for example be that certain properties become true and certain properties become false,possibly bringing the system to an undesired state.Because in a self-organizing multi-agent system local rules work as guidance for agents to behave thus leading to specific outcomes,we can see the set of local rules as a mechanism that we implement in the system.A mechanism is a procedure,protocol or game for generating desired outcomes.If we want to know whether we can design a set of local rules to ensure desired outcomes,we then enter the field of mechanism design.([7])In the area of model checking,some work has been done to verify a multi-agent system,where norms are regarded as a mechanism.M.Knobbout et al.assume agents to have some preferences,which might be unknown to the system designers,and use a solution concept of Nash equilibrium for decision-making.([4])A formal framework is developed to verify whether a normative system implements desired outcomes no matter what preferences agents have.N.Bulling and M.Dastani formally analyze and verify whether a specific behavior can be enforced by norms and sanctions if agents follow their subjective preferences and whether a set of norms and sanctions that realize the effect exists at all.([2])In the present paper,agents are supposed to communicate with each other for their internals,which might be unknown to the system designers when the system is operated in an open environment,and thus it is important to know how the system behaves under the change of agents’ internals.Intuitively,we can verify both the original system and the new system afresh.However,as we have proved in [6],the verification is computationally expensive.Therefore,we need to think about how we can properly use the verification result that we get from the original system to better verify the new system.In this paper,we propose a framework to reason about the dynamics of self-organizing multi-agent systems under the change of participating agents.Agents follow their local rules to communicate with each other and perform actions,which results in the structural and semantic independence between agents that are represented by the notion of full contributions to the global system behavior.We prove that the full contribution of a coalition of agents remains the same if the internal function of any agent in the coalition is unchanged.Furthermore,we prove that the properties of a coalition regarding not being semantically independent or structurally independent inherit from the original system to the new system if the internal function of any agent in the coalition is unchanged,which means that we do not need to check their semantic independence and structural independence when verifying the new system.Such results can be used to improve the verification efficiency for the new system.

The remaining part of this paper is structured as follows:In Section 2,we introduce the framework we use in this paper,setting up the context of self-organizing multi-agent systems;In Section 3,we propose the way how we change participating agents and prove what verification information we can use from the original system to efficiently verify the new system;In Section 4,we provide an example to illustrate our results;In Section 5,we conclude this paper and provide future work.

2 Framework

We use the same framework to formalize self-organizing multi-agent systems as what we introduced in[6].The semantic structure of this paper is concurrent game structures (CGSs).It is basically a model where agents can simultaneously choose actions that collectively bring the system from the current state to a successor state.Compared to other kripke models of transaction systems,each transition in a CGS is labeled with collective actions and the agents who perform those actions.Moreover,we treat actions as first-class entities instead of using choices that are identified by their possible outcomes.Formally,

Definition 1A concurrent game structure is a tupleS(k,Q,π,Π,ACT,d,δ)such that:

• A natural numberk ≥1 of agents,and the set of all agents is Σ{1,...,k};we useAto denote a coalition of agentsA ⊆Σ;

• A finite setQof states;

• A finite set Π of propositions;

• A labeling functionπwhich maps each stateq ∈Qto a subset of propositions which are true atq;thus,for eachq ∈Qwe haveπ(q)⊆Π;

• A finite setACTof actions;

• For each agenti ∈Σ and a stateq ∈Q,di(q)⊆ACTis the non-empty set of actions available to agentiinq;D(q)d1(q)×...×dk(q)is the set of joint actions inq;given a stateq ∈Q,an action vector is a tuple〈α1,...,αk〉such thatαi ∈di(q);

• A functionδwhich maps each stateq ∈Qand a joint action〈α1,...,αk〉 ∈D(q) to another state that results from stateqif each agent adopted the action in the action vector,thus for eachq ∈Qand each〈α1,...,αk〉 ∈D(q)we haveδ(q,〈α1,...,αk〉)∈Q,and we use(q,〈α1,...,αk〉,q′)whereq′δ(q,〈α1,...,αk〉)to denote a transition that starts fromqand is labeled with〈α1,...,αk〉.

Note that the model is deterministic:the same update function adopted in the same state will always result in the same resulting state.A computation overSis an infinite sequenceλq0,q1,q2,...of states such that for all positionsi ≥0,there is a joint action〈α1,...,αk〉 ∈D(qi) such thatδ(qi,〈α1,...,αk〉)qi+1.For a computationλand a positioni ≥0,we useλ[i]to denote theith state ofλ.More elaboration of concurrent game structures can be found in[1].

The same as what we did in [6],we can define a self-organizing multi-agent system as a concurrent game structure together with a set of local rules for agents to follow.Before defining such a type of local rules,we first define what to communicate,which is given by an internal function.

Definition 2(Internal Functions) Given a concurrent game structureSand an agenti,the internal function of agentiis a functionmi:Q →Lpropthat maps a stateq ∈Qto a propositional formula.We use a tupleM〈m1,m2,...,mk〉to denote the profile of internal functions for all the participating agents.We also useUito denote the set of possible internal functions for agentiin Σ andUMU1×U2×...Ukto denote the universe of tuples of internal functions.

The internal function returns the information that is provided by participating agents themselves at a particular state,which is referred to as anagent typein this paper and thus might be different from agent to agent.A local rule is defined based on agents’communication as follows:

Definition 3(Abstract Local Rules) Given a concurrent game structureS,an abstract local rule for agentais a tuple〈τa,γa〉consisting of a functionτa(q)that maps a stateq ∈Qto a subset of agents,that is,τa(q)⊆Σ,and a functionγa(M(q))that mapsM(q){mi(q)|i ∈τa(q)}to an action available in stateqto agenta,that is,γa(M(q))∈da(q).We denote the set of all the abstract local rules as Γ and a subset of abstract local rules as ΓAthat are designed for the coalition of agentsA.

An abstract local rule consists of two parts:the first partτa(q)states the agents with whom agentais supposed to communicate in stateq,and the second partγastates the action that agentais supposed to take given the communication with agents inτa(q)for their internals.We see local rules not only as constraints but also guidance on agents’behavior,namely an agent does not know what to do if he does not communicate with other agents.Therefore,we exclude the case where agents get no constraint from their respective local rules.We useoutto denote a set of computations and notationout(q,M,ΓA)is the set of computations starting from stateqwhere agents in coalitionAfollow their respective local rules in ΓAwith internal functionsM.A computationλq0,q1,q2,...is inout(q0,M,ΓA) if and only if it holds that for all positionsi ≥0 there is a move vector〈α1,...,αk〉 ∈D(λ[i])such thatδ(λ[i],〈α1,...,αk〉)λ[i+1]and for alla ∈Ait is the case thatαaγa(M(λ[i])).Moreover,when we refer to a stateqin a computationλ,which is inout(q0,M,ΓA),we will simply writeq ∈out(q0,M,ΓA)for short in the rest of this paper.Now we are ready to define a self-organizing multi-agent system.Formally,

Definition 4(Self-organizing Multi-agent Systems) A self-organizing multi-agent system(SOMAS)is a tuple(S,M,Γ),whereSis a concurrent game structure,Mis the set of internal functions and Γ is a set of local rules that agents follow.

Example 5We will use the example in[3,11]for better understanding the above definitions.Consider a CGS scenario as Figure.1 where there are two trains,each controlled by an agent,going through a tunnel from the opposite side.The tunnel has only room for one train,and the agents can either wait or go.Starting from stateq0,if the agents choose to go simultaneously,the trains will crash,which is stateq4;if one agent goes and the other waits,they can both successfully pass through the tunnel,which isq3.

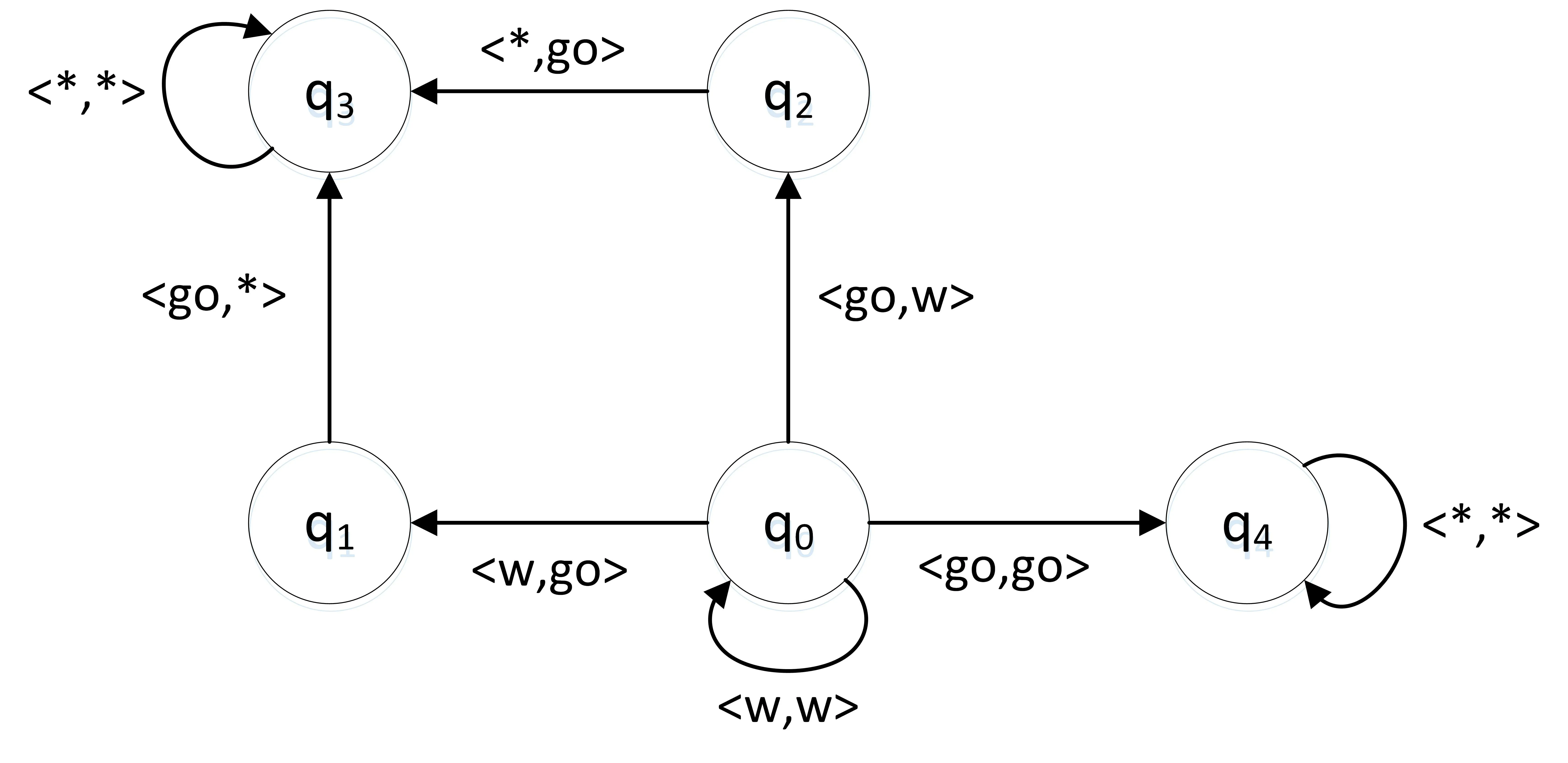
Fig.1:A CGS example.

Local rules〈τ1,γ1〉and〈τ2,γ2〉are prescribed for the agents to follow:both agents communicate with each other for their urgenciesu1andu2in stateq0;the one who is more urgent can go through the tunnel first;otherwise,it has to wait.Given the above local rules,ifa1is more urgent than or as urgent asa2with respect tou1andu2,the desired stateq3is reached along with computationq0,q2,q3...;ifa1is less urgent thana2with respect tou1andu2,the desired stateq3is reached along with computationq0,q1,q3....

In order to study how a self-organizing multi-agent system behaves under the change of participating agents,we first need to characterize the independence between agents in terms of their contributions to the system behavior.In this paper,it is characterized from two perspectives:a semantic perspective given by the underlying game structure and a structural perspective derived from abstract local rules.Similar to ATL in [1],our language ATL-Γ is interpreted over a concurrent game structureSthat has the same propositions and agents as our language.It is an extension of classical propositional logic with temporal cooperation modalities.A formula of the form〈A〉ψmeans that coalition of agentsAwill bring about the subformulaψby following their respective local rules in ΓA,no matter what agents in ΣAdo,whereψis a temporal formula of the form○φ,□φorφ1Uφ2(whereφ,φ1,φ2are again formulas in our language).Formally,the grammar of our language is defined below,wherep ∈Π andA ⊆Σ:

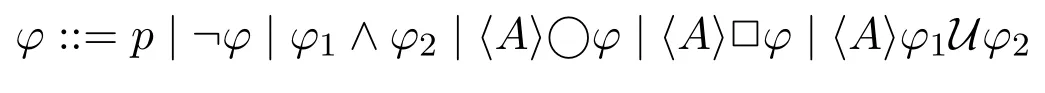
Given a self-organizing multi-agent system(S,M,Γ),whereSis a concurrent game structure and Γ is a set of local rules,and a stateq ∈Q,we define the semantics with respect to the satisfaction relation|inductively as follows:

•S,M,Γ,q |piffp ∈π(q);

•S,M,Γ,q |¬φiffS,M,Γ,q|φ;

•S,M,Γ,q |φ1∧φ2iffS,M,Γ,q |φ1andS,M,Γ,q |φ2;

•S,M,Γ,q |〈A〉○φiff for allλ ∈out(q,M,ΓA),we haveS,M,Γ,λ[1]|φ;

•S,M,Γ,q |〈A〉□φiff for allλ ∈out(q,M,ΓA)and all positionsi ≥0 it holds thatS,M,Γ,λ[i]|φ;

•S,M,Γ,q |〈A〉φ1Uφ2iff for allλ ∈out(q,M,ΓA)there exists a positioni ≥0 such that for all positions 0≤j ≤iit holds thatS,M,Γ,λ[j]|φ1andS,M,Γ,λ[i]|φ2.

Dually,we write〈A〉◇φfor〈A〉⊤Uφ.We can check a formula in our language to verify whether a coalition of agents will bring about a temporal property through following its local rules,which is regarded as semantic independence in this paper.Moreover,agents in the system follow their respective local rules to communicate with other agents.Based on their communcation,we can see a coalition of agents do not get input information from agents outside the coalition,which is regarded as structural independence in this paper.This gives rise to the notion of independent components.

Definition 6(Independent Components) Given an SOMAS(S,M,Γ),a coalition of agentsA ⊆Σ and a stateq,we say that coalitionAis an independent component w.r.t.qif and only if for alla ∈Aand its abstract local rule〈τa,γa〉it is the case thatτa(q)⊆A;a coalition of agentsAis an independent component w.r.t.a set of computationsoutiff for allλ ∈outandq ∈λ,Ais an independent component with respect to stateq.

In other words,an independent component might output information to agents in ΣA,but do not get input from agents in ΣA.As we can see,it is a structural property given by the communication between agents in a given state.We then propose the notions ofsemantic independence,structural independence and full contributionto characterize the independence between agents from different perspectives.

Definition 7(Semantic Independence,Structural Independence and Full Contribution) Given an SOMAS(S,M,Γ),a coalition of agentsAand a stateq,

•Ais semantically independent with respect to a temporal formulaψfromqiffS,M,Γ,q |〈A〉ψ;

•Ais structurally independent fromqiffAis an independent component w.r.t.the set of computationsout(q,M,ΓA);

•Ahas full contribution toψinqiffAis the minimal(w.r.t.set-inclusion)coalition that is both semantically independent with respect toψand structurally independent fromq.

In other words,coalitionAhas full contribution toψbecause any subset of coalitionAis either semantically dependent with respect toψor structurally dependent.Given a self-organizing multi-agent system and a set of temporal formulas,we check with each subset of agents and each temporal formula for their semantic and structural independence in order to find which coalition has full contribution to which property.One can refer to[6]for detailed discussion about the above definitions and examples in this section.

Example 8We continue to discuss the two-train example.Neither train,namelya1ora2as a coalition,has full contribution to the result of passing through the tunnel without crash.The reasons are listed as follows:any single train cannot ensure the result of passing through the tunnel without crash,which means that any single train is not semantically independent and can be expressed:

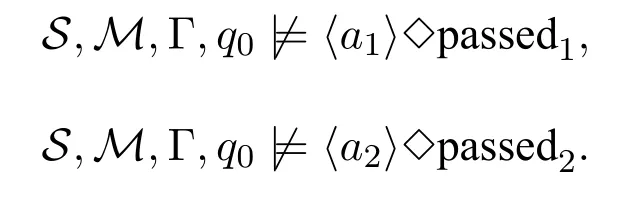
Moreover,both trains follow their local rules to communicate with each other in stateq0,which means that any single train is not an independent component w.r.t.stateq0thus not being structurally independent.

Two trains have full contribution to the result of passing through the tunnel without crash,because both agents by themselves can bring about the result of passing through the tunnel without crash through following the local rules,which can be expressed:

Moreover,the coalition of two trains is obviously an independent component w.r.t.out(q0,M,Γ{a1,a2}),which means that it is structurally independent,and the coalition of two trains is obviously the minimal coalition that is both semantically independent w.r.t.the result of passing the tunnel without crash and structurally independent from stateq0.

3 Changing Participating Agents

When a self-organizing multi-agent system is deployed in an open environment,different types of agents participate in the system and their internals might be unknown to system designers.Therefore,it is important to verify whether the set of local rules still generates desired outcomes,more generally how the system behaves,under the change of participating agents.Because in this paper an internal functionmirefers to an agent type and might be interpreted as agents’preferences,interests or other internal information over states that can be different from agent to agent,changing participating agents can be done by simply replacing internal functions so that the original internal function and the new internal function return different values in the same state.Here we assume that the number of agents in the system does not change so the indexes of agents in Σ remain the same.We have the following definition:

Definition 9(Change of Participating Agents) Given an original SOMAS(S,M,Γ),a new SOMAS under the change of participating agents is denoted as(S,M′,Γ),whereM′ ∈UMand there exists an agenta ∈Σ and a stateq ∈Qsuch thatma(q)

As we can see,what we meant by replacing internal functions is that in the new system there exists at least an agent’s internal function such that given the same state its output is different from the one in the original system.Except the internal functions,the underlying concurrent game structure and the set of local rules remain the same.

Changing participating agents in the system might cause undesired outcomes.Agents communicate with each other for their internals and make a move based on the communication results.The change of agents’ internal functions might change the actions that agents are allowed to take by their local rules,and consequently the new system runs along a computation that might be different from the original system,making undesired properties hold.Therefore,local rules have to be well designed in order to ensure that desired properties remain unchanged under the change of participating agents.

Example 10In the two-train example,suppose both trains have the same urgency,denoted asM′,they will choose to wait because neither train is more urgent than the other one,resulting in the undesired stateq0of deadlock.As we can see,the local rules cannot ensure that the system reaches a desired state no matter what kind of agents participate in the system.

Given a self-organizing multi-agent system(S,M,Γ)and a temporal formula as an indicated property,in order to find out which coalition of agents has full contribution to a temporal formula,we need to do model-checking with each subset of Σ and that formula.Intuitively we can follow the same process to verify the new system (S,M′,Γ) as what we did with the original system.However,as we have proved in[6],checking whether a coalition of agents has full contribution to a temporal formula is computationally expensive,because we have to enumerate all the subsets of the coalition and check for their semantic and structural independence in order to ensure the minimality,making verifying both the original system and the new system afresh inefficient and difficult.Thus,it is important to think about whether we can use the verification result with the original system to better verify the new system.In the area of formal argumentation,Beishui Liao,et al propose a divisionbased method to compute the status of arguments when the argumentation system is updated.([5]) Inspired by that,we can divide the system into two parts:the set of agents whose internal functions remain the same and the set of agents whose internal functions change.For the first part,as was in Definition 9,when a self-organizing multi-agent system switches to another under the change of participating agents,it is not necessary that the internal functions of all agents change,which means that there might exist some agents whose internal functions remain the same.Such agents are called an unchanged set.Formally:

Definition 11(Unchanged Sets) Given two SOMASs (S,M,Γ) and (S,M′,Γ)under the change of agents’internal functions fromMtoM′,an unchanged set with respect toMandM′is defined asUS(M,M′){a ∈Σ|for allq ∈Q:ma(q)

An unchanged set is symmetric in terms of the change of agents’internal functions.

Proposition 12Given two SOMASs (S,M,Γ) and (S,M′,Γ),US(M,M′)US(M′,M).

ProofWe can easily prove it following Definition 11. □

A coalition of agents has full contribution to a temporal formula if and only if it is the minimal coalition that is both structurally and semantically independent.We can intuitively imagine that a coalition behaves the same if the internal function of each agent inside the coalition does not change,which means that we can reuse the verification information for the original system when verifying the new system.Thus,one important property of unchanged sets is that the full contributions of agents inside an unchanged set remain the same when the internal functions switch fromMtoM′.

Proposition 13Given two SOMASs(S,M,Γ)and(S,M′,Γ)under the change of agents’internal functions fromMtoM′,and a stateq,if for anya ∈A,q′ ∈Q,i ∈τa(q′)it is the case thatmi(q′),thenout(q,M,ΓA)out(q,M′,ΓA).

ProofLetout(q,M,ΓA)[i] be a set of states,each of which is theith state of any computation inout(q,M,ΓA).That is,out(q,M,ΓA)[i]{q′ ∈Q | ∃λ ∈out(q,M,ΓA) :q′λ[i]}.Next,we need to inductively prove thatout(q,M′,ΓA)in the new system contains the same computations asout(q,M,ΓA) in the original system.Firstly,computations from bothout(q,M,ΓA)andout(q,M′,ΓA)start from stateq.Secondly,supposeout(q,M,ΓA)[i]out(q,M′,ΓA)[i].If for anya ∈A,q′ ∈Q,i ∈τa(q′)we havemi(q′)m′i(q′),thenM(q′)M′(q′),consequentlyγa(M(q′))γa(M′(q′)),which means thatγa(·)returns the same action for each agent in stateq′in both systems.Hence,out(q,M,ΓA)[i+1]out(q,M′,ΓA)[i+1].So we can conclude thatout(q,M,ΓA)out(q,M′,ΓA). □

From that,we can see the properties of computation setout(q,M,ΓA)remain the same under the change of agents’internal functions fromMtoM′if the internal functions of agents with which coalitionAneeds to communicate remain the same.This gives rise to one important property of unchanged sets:the full contributions of agents inside an unchanged set remain the same when the internal functions switch fromMtoM′.

Theorem 14.Given two SOMASs(S,M,Γ)and(S,M′,Γ)under the change of agents’ internal functions from M to M′,for any coalition A ⊆US(M,M′),A has full contribution to a temporal formula ψ in a state q in(S,M,Γ)iff A has full contribution to ψ in q in(S,M′,Γ).

ProofWe first prove the forward part.Because coalitionAhas full contribution toψin stateqin SOMAS (S,M,Γ),we haveS,M,Γ,q |〈A〉ψ(semantic independence),andAis an independent component w.r.t.out(q,M,ΓA) (structural independence),and any subset ofAis either semantically dependent with respect toψor structurally dependent from stateqin(S,M,Γ).BecauseA ⊆US(M,M′),the internal function of any agent inAremains the same fromMtoM′.By Proposition 13,out(q,M,ΓA)out(q,M′,ΓA).That implies the properties that hold forout(q,M,ΓA) also hold forout(q,M′,ΓA).Thus,by Definition 7,we haveS,M′,Γ,q |〈A〉ψ(semantic independence),andAis an independent component w.r.t.out(q,M′,ΓA) (structural independence).Next,we need to prove whetherAis also the minimal coalition that is both semantically independent with respect toψand structurally independent fromqin(S,M′,Γ).Suppose there exists a coalitionA′ ⊂Athat is both semantically independent with respect toψand structurally independent fromqin(S,M′,Γ),which means thatS,M′,Γ,q |〈A′〉ψandA′is an independent component w.r.t.out(q,M′,ΓA′).BecauseA′ ⊂A ⊆US(M,M′)US(M′,M),the internal function of any agent inA′remains the same fromM′toM.By Proposition 13,out(q,M,ΓA′)out(q,M′,ΓA′),which implies thatS,M,Γ,q |〈A′〉ψandA′is an independent component w.r.t.out(q,M,ΓA′)and thus contradicts with the premise thatAis the minimal coalition that is both semantically independent and structurally independent.Hence,coalitionAis also the minimal coalition that is semantically independent w.r.t.ψand structurally independent from stateqin the new system.Therefore,coalitionAalso has full contribution toψin stateqin(S,M′,Γ).BecauseA ⊆US(M,M′)US(M′,M),we can prove the backward part in a similar way. □

Therefore,given that the internal functions of coalitionAremain the same,if we already know that coalitionAhas full contribution toψin stateqin the original system,it will remain the same in the new system;if we already know that coalitionAdoes not have full contribution toψin stateqin the original system,it will also remain the same in the new system.That means the verification information regarding agents in the unchanged set will remain the same under the change of agents’internal functions,which can be used to simplify the verification of the new system.To find the unchanged set with respect toMandM′,we can simply check the internal functions of all the agents with all the states,which can be done in polynomial time to the number of states and the number of agents.After we obtain the unchanged set,we can copy the information about agents’ full contributions within the unchanged set from the original system to the new system.Moreover,since the full contributions of agents in the unchanged set remain the same,the coalitions that we have to check with for the new system becomeP(Σ)P(US(M,M′))instead ofP(Σ)for the original system.The propositions below will give insights to further simplify the verification of the new system.

Proposition 15Given an SOMAS(S,M,Γ),a coalition of agentsA,a temporal formulaψand a stateq,if for anyA′ ⊆Ait is the case thatA′does not have full contribution toψin stateq,thenA′is either semantically dependent w.r.t.ψor structurally dependent fromq.

ProofSuppose there existsA′ ⊆Asuch that it is both semantically independent w.r.t.ψand structurally independent fromq.IfA′is the minimal one,A′has full contribution toψin stateq;ifA′is not the minimal one,there existsA′′ ⊂A′such that it is the minimal coalition that is both semantically independent w.r.t.ψand structurally independent fromq.Both cases contradict with the premise that for anyA′ ⊆Ait is the case thatA′does not have full contribution toψin stateq.Thus,A′is either semantically dependent w.r.t.ψor structurally dependent fromq. □

Theorem 16.Given two SOMASs(S,M,Γ)and(S,M′,Γ)under the change of agents’internal functions from M to M′,a coalition of agents A⊆US(M,M′),a temporal formula ψ and a state q,A has full contribution to ψ in state q in(S,M′,Γ)iff both of the following statements are satisfied:

1.for any A′ ⊆US(M,M′)∩A it is the case that A′ does not have full contribution to ψ in state q in(S,M,Γ);

2.A is the minimal(w.r.t.set-inclusion)coalition within P(A)P(US(M,M′))that is both semantically independent with respect to ψ and structurally independent from q in(S,M′,Γ).

ProofSince for anyA′ ⊆US(M,M′)∩Ait is the case thatA′does not have full contribution toψin stateqin(S,M,Γ),we then have for anyA′ ⊆US(M,M′)∩Ait is the case thatA′does not have full contribution toψin stateqin(S,M′,Γ).That also impliesA′is either semantically dependent w.r.t.ψor structurally dependent from stateqin(S,M′,Γ).Combining with the second statement,we can conclude thatAhas full contribution toψin stateqin(S,M′,Γ). □

In order to verify whether a coalition of agentsAhas full contribution toψ,normally we have to check the semantic independence and structural independence of any subset ofAin order to ensure the minimality,which is computationally expensive as the size of the coalition increases.While Theorem 14 shows us the case whereA ⊆US(M,M′),Theorem 16 shows us how we can further utilize the information about agents’full contribution from the original system in the new system whenA⊆US(M,M′).If we have proved that any subset of the unchanged set does not have full contribution toψin the original system,we do not need to check their semantic independence and structural independence when verifying the new system,because they will not hold as in the original system.With the verification information from the original system,we can decrease the coalitions that we have to check fromP(A)toP(A)P(US(M,M′)∩A).We can use Theorem 16 and Theorem 14 to more efficiently verify whether a coalition of agents has full contribution to a temporal formula in the new system.In the next section,we will use an example to illustrate how we can use the verification result from the original system in the verification of the new system based on Theorems 14 and 16.

4 Example

We extend the two-train example to illustrate the above theory.Suppose we have a U-shape traffic system depicted as in Fig.2.The top is the same as the previous example where trainsa1anda2,each controlled by an agent,are going through a tunnel from the opposite side.Agenta2exits the traffic system from Exit1 after passing through the tunnel,while agenta1needs to go down to exit the traffic system from Exit3 after passing through the tunnel.Below the tunnel there is a second tunnel,and on the left hand side another train,controlled by agenta3,is also going through the tunnel to exit the system from Exit3.The whole traffic system has only room for one train to go through,and the agents can either wait or go.Since agenta1needs to go down to exit the traffic system after passing through the first tunnel,it will clash with agenta3by Exit3 if they go simultaneously.The CGS is depicted in Fig.3.

Fig.2:A traffic system consisting of three trains.

Fig.3:CGS of the three-train example,where formula ci means that train i clashes in the tunnel and formula ei means that train i exits the traffic system.

The local rules for three agents are quite simple:whenever there is space limitation for two trains to go through,the one which is more urgent can go first and the other one which less urgent needs to wait.The set of temporal formulas is{◇e1,◇e2,◇e3},each of which means that agentiexits the system.Given an SOMAS(S,M,Γ),suppose agenta2is more urgent than agenta1,so agenta1waits until agenta2passes through the first tunnel.Because agenta3goes while agenta1is waiting,agenta3can exit the system without meeting agenta1by the Exit3.Thus,we have the following verification information in Table 1.From Table 1 we can see that coalition{a1,a2}has full contribution to the result of◇e1and◇e2in stateq0in(S,M,Γ)as what we had previously,and{a1,a2,a3}has full contribution to◇e3in stateq0in(S,M,Γ).In particular,agenta3cannot bring about the result of exiting the system by itself,because ifa1goes anda2waits,which means that they do not follow their local rules to behave,a1anda3will meet Exit3 and need to cooperate in order to exit the system.

Table.1:Verification information for SOMASs (S,M,Γ),where“SI”stands for structural independent.

Table.2:Verification information for SOMAS (S,M′,Γ),where“SI”stands for structural independent.

Now consider a new SOMAS(S,M′,Γ)under the change of internal functions fromMandM′,where the internal functions of agentsa1anda2change while the internal function of agenta3remains the same.In this case,agenta1chooses to go and agenta2chooses to wait.We can see thata1anda3will meet by Exit3 and thus they need to communicate with each other for their urgencies.Moreover,since only the internal function ofa3remains the same,and coalitions{a3}and∅do not have full contribution to◇e1,◇e2or◇e3in the original system(S,M,Γ),by Theorem 16,we can reuse the verification information about{a3}from the original system by copying the columns of∅and{a3}from Table 1 to Table 2.It shows that{a3}and∅are either semantically dependent or structurally dependent.Copying this information can simplify the process of ensuring the minimality when doing modelchecking.For example,for checking whether coalition{a1,a2,a3}has full contribution to◇e3in stateq0in (S,M′,Γ),normally we need to check both semantic and structural independence for each subset of{a1,a2,a3},which isP({a1,a2,a3});since we know from the original system that∅and{a3}are either semantically dependent w.r.t.◇e3or structurally dependent,the coalitions we need to check becomeP({a1,a2,a3}){∅,{a3}}.We then have the following verification information in Table 2.As we can see,coalition{a1,a2,a3}is the minimal coalition that is both semantically independent(w.r.t.◇e1,◇e2or◇e3)and structurally independent,so coalition{a1,a2,a3}has full contribution to◇e1,◇e2and◇e3in stateq0in(S,M′,Γ).

5 Conclusion

When a self-organizing multi-agent system is deployed in an open environment,the change of participating agents might bring the system to an undesired state.As it is computationally expensive to verify a self-organizing multi-agent system,we need to think about how we can properly use the verification result that we get from the original system to better verify the new system.In this paper,we propose a framework to reason about the dynamics of self-organizing multi-agent systems under the change of participating agents.Agents in the system are divided into two parts:one whose internal functions remain the same and the other one whose internal functions change.We first proved that the full contribution of a coalition of agents remains the same if the internal function of any agent in the coalition remains the same.Furthermore,the properties of a coalition regarding not being semantically independent or structurally independent remain the same if the internal function of any agent in the coalition remains the same,which means that we do not need to check their semantic independence and structural independence when verifying the new system.Future work can be done in the direction of reasoning about the dynamics of self-organizing multi-agent systems in terms of revising agents’local rules.