一种改进的网格剖分协方差交集融合算法∗

（中国电子科技集团公司第十研究所 成都 610036）

1 引言

分布式多传感器数据融合技术是各节点利用本地传感器量测获取目标状态的局部估计，继而与其他节点进行交互，利用融合算法获得全局目标状态估计。通过数据融合技术给出对目标位置的精确估计，从而改善对目标的跟踪和识别［1～3］。与传统集中式融合相比，分布式融合对系统资源要求较低，可靠性和扩展性更好，因此在工程实际中发挥着越来越多的作用。

在多传感器数据融合领域已经发展了很多算法和融合规则，文献［4～7］对协方差凸组合方法进行了讨论。协方差凸组合算法没有考虑局部航迹的相关性，抗干扰能力较弱，造成其算法的鲁棒性较差，仅仅在局部航迹完全独立的情况下是最优的。此外，文献［5］中Bar-Shalo-Campo融合算法考虑了共同的过程噪声的相关性，然而为了计算各传感器估计误差之间的互协方差阵而需要大量的信息，在最小均方误差意义下不是最优的。在分布式系统中，常常无法准确描述多源信息之间的相关性，文献［8～10］提出了协方差交叉算法。协方差交叉是一种保守融合方法，无论局部航迹之间的相关性如何，都可以用一个协方差椭圆逼近局部航迹的协方差椭圆的交集。

协方差交集类方法的重点与难点是求两个协方差椭圆的交集，文献［11］用优化的方法近似求出椭圆的交集，文献［12］从工程实际出发，直接用网格剖分的几何方法求出两个椭圆的交集，用交集内的网格求出两个椭圆的交集。但这种方法没有考虑局部椭圆不是轴对称的情况，本文从实际出发，基于交集内的网格，近似求出融合椭圆的长轴和短轴，从而求出融合椭圆。这种方法具有更好的适用性，能够满足工程应用的需求。

2 协方差交叉融合算法

协方差交叉融合是有两个相关估计量X1，X2进行数据融合，以得到最优融合估计量X及协方差阵的估计阵P，两个相关估计量之间的相关性P12未知。均值与协方差估计值分别为和{X2，P2}。

假设估计的唯一约束条件就是一致性：

一般情况下，协方差交集是对均值和协方差估计的一个凸组合，其算法过程为

0≤ω≤1是权值。ω决定了分配给两个相关估计量的权值。根据不同的标准来选择使用不同的ω进行优化。可以选择P的迹、特征值也可以是行列式。由于行列式不受状态量单位的影响，同时也充分利用了所有元素提供的信息，因此采用行列式更好一些。文献［11］提供了一个优化P行列式的算法：

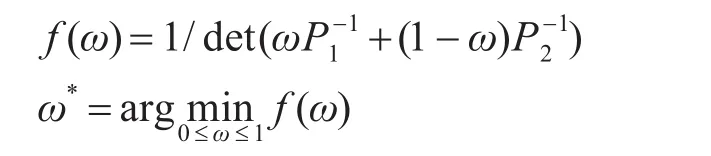
此时在不清楚相关度P12时，也能给出一个改进的预测值。

3 网格剖分的协方差交叉融合算法

基于网格剖分的协方差交集融合算法，参考文献［12］，首先利用几何法对位置空间进行网格剖分，求出局部航迹协方差椭圆所包含的网格集合，其次，对所有的网格集合进行与运算，求出局部航迹协方差椭圆所包含的公共网格集合。最后利用公共网格集合拟合融合误差协方差椭圆逼近协方差椭圆的交集，从而求出融合估计值及融合误差协方差。由于文献［12］只对轴对称的椭圆进行了处理，不适用于X和Y方向向量相关的情形。算法步骤如下：

1）网格剖分，将平面划分为边长为h的矩形网络，位置 (xi，yi)与网格 π(i，j)的映射关系如下：

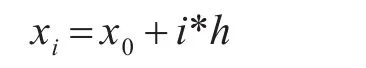
yi=y0+i*h，其中 (x0，y0)为平面原点。

2）协方差椭圆表示

设点(x，y)的估计均值和协方差矩阵分别为(xˉ，yˉ)与P。当网格对应的位置落在协方差椭圆内的充要条件为满足如下公式：

其中k是指定常数。

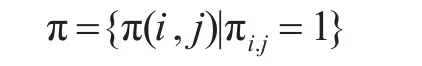
3）协方差椭圆交集的表示

n表示有n个椭圆相交。

4）融合估计值的求法

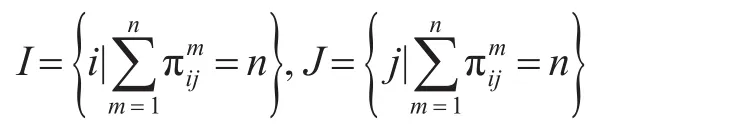
则I，J分别表示为x，y方向协方差交集剖分的网格下标集合，则估计值为

x，y方向的方差分别为

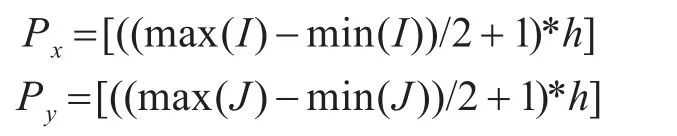
此算法无法求出Pxy，没有考虑协方差椭圆不是轴正交的情况。而在实际应用中由于传感器的量测坐标系转换到笛卡尔坐标系中时，x和y方向分量往往是相关的。此时，可以先根据公共网格计算融合椭圆的中心及近似长轴，公共网格区域的面积近似为融合椭圆的面积，根据椭圆面积公式求出椭圆的短轴。从而计算融合的误差协方差。

椭圆的中心近似为

椭圆面积近似为s=|I|*h2。

椭圆的短轴近似为b=s/(π*a)。

4 仿真

4.1 误差椭圆分析

依次局部航迹估计1，局部航迹估计2，网格剖分的协方差交叉融合算法，基于行列式的协方差交叉融合算法，改进的网格剖分的协方差交叉融合算法误差椭圆，如图1所示。

如上图所示，本文的改进算法的均值与原始网格剖分的协方差交叉融合算法的均值相同，都很接近航迹1和航迹2均值的平均值，本文方法的误差椭圆能更好地逼近协方差椭圆的交集。

4.2 蒙特卡洛仿真

假设目标先以200m/s的速度做20s匀速运动，然后以角速度4.096°/s的角速度做60s匀速转弯运动，目标运动真实轨迹如图2所示。

假设两个局部航迹，噪声分别是50m和100m的正态分布噪声，当两个局部航迹噪声完全相关，噪声分布在真实航迹两边，经50次蒙特卡罗仿真统计协方差凸组合融合，优化行列式的协方差交集融合，改进的网格剖分的协方差方法的均方根误差，如图3所示。

图2 目标运动真实轨迹

当两个局部航迹的噪声完全独立，经50次蒙特卡罗仿真统计协方差凸组合融合、优化行列式的协方差交集融合，改进的网格剖分的协方差方法的均方根误差，如图4所示。

图4 噪声完全独立时融合误差均方根误差比较

5 结语

本文针对网格剖分进行协方差交叉融合中椭圆逼近的问题进行了探索和改进。用Matlab软件进行了蒙特卡罗仿真。仿真结果表明，改进的网格剖分算法比文献［12］中的网格剖分算法及基于行列式优化的协方差融合算法和协方差凸组合算法效果更好。