矩阵分块方法在协方差矩阵中的应用
冯 岩, 宋 珊, 张子明, 徐常青
(苏州科技大学 数学科学学院,江苏 苏州215009)
协方差矩阵是多元统计学中的基本概念,它反映多变量之间的线性相关性及变量分布离散程度。 方差测量单个随机变量的变化(比如一个群体中人的身高变化),而协方差则是衡量两个随机变量的变化程度(如一个群体中的一个人的身高和体重的变化情况)。 Magnus J R 在1978 年提出了在干扰协方差矩阵中具有未知参数的GLS 模型的最大似然估计[1],Meng X 等人在1991 使用EM 获得渐近方差协方差矩阵[2],Odell P L等人在1966 年提出了生成样本协方差矩阵的数值程序[3],Danaher P 等人在2012 年提出了用Lasso 方法对协方差矩阵的逆进行估计[4]。 矩阵的理论发展也非常迅速,在19 世纪末,矩阵理论体系已基本形成。 到20 世纪,矩阵理论得到了进一步的发展。 目前,它已经发展成为在物理学、控制论、机器人学、生物学、经济学等学科有大量应用的数学分支。 而矩阵理论在统计中主要用于估计线性模型的参数、对估计和模型进行比较和利用矩阵的广义逆研究随机向量之间的关系等。 分块矩阵是处理阶数较高的矩阵时常采用的技巧,也是数学在多领域的研究工具。 对矩阵进行适当分块,可使高阶矩阵的运算转化为低阶矩阵的运算,同时也使原矩阵的结构显得简单而清晰,从而能够大大简化运算步骤,或给矩阵的理论推导带来方便。 笔者主要运用矩阵分块理论对协方差矩阵进行研究。
协方差矩阵反映随机变量离散度及不同变量线性相关性的一类重要的二维统计参数,其对角元为相应变量方差,而非对角元为相应两个变量间的协方差,它反映变量之间的线性相关性。 统计与概率论专家威廉·费勒把协方差矩阵称为随机向量的方差。
协方差阵分为总体协方差阵和样本协方差阵。 总体协方差矩阵(population covariance)一般记为Σ=(σij),它通常为未知参数阵,样本协方差矩阵(sample covariance)也称为样本散度矩阵(dispersion matrix),一般记为SN(N 为样本点个数)。 已知样本情形下SN可计算,由此可对总体协方差矩阵进行估计,即SN≈Σ。一般情况下,样本点个数越大,近似效果越好。 但这种近似效果好坏不仅取决于样本点个数,它还依赖于母体分布和取样方式。 另一方面,很多情况下足够大的N 不仅增加取样成本,而且不现实。 如人类在观察星云系亮度变化、海平面变化规律、地球生物物种变化与气候环境的关系时,获取的样本观察值个数有限,这时就需要通过其他方式(如母体概率分布假设和已知变量相关性等)来对总体协方差矩阵进行估计。
假设有随机变量x 和y,且对应有N 个样本点(x1,y1),(x2,y2),…,(xN,yN)。 那么随机变量x 的样本方差(散度)为
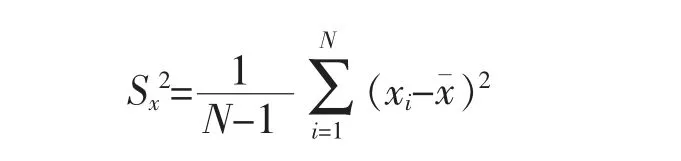
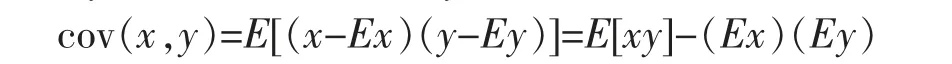
若x=y,则记var(x)=cov(x,x)=σx2=σ2(x)。 显然σx2≥0,且有
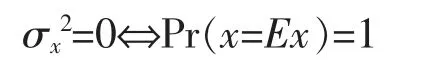
现考虑n 维随机向量x,y∈Rn。 则x 和y 对应的样本协方差为
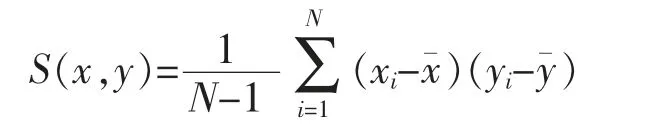
利用协方差矩阵奇异值分解(SVD),可求出高维数据点分布的主成分及其在其不同主成分方向上的投影的方差。若随机向量x 对应的协方差矩阵为奇异,那么随机变量x1,x2,…,xn具有一定的线性相关性。这时随机变量出现冗余,可通过对应协方差矩阵的分块来研究其冗余性,从而简化对应的回归模型。
1 协方差矩阵及其性质
设x1,x2,…,xn为n 个随机变量,那么x=(x1,x2,…,xn)T为n 维随机向量。 记A=(aij)∈Rn×n为x 对应的协方差矩阵,即
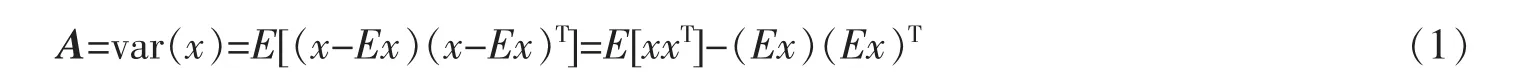
显然AT=A(aij=aji,∀(i,j)),即A 为实对称矩阵。 不难证明A 为一个Gram 矩阵,即存在一组向量β1,β2,…,βn∈RK,使


其中
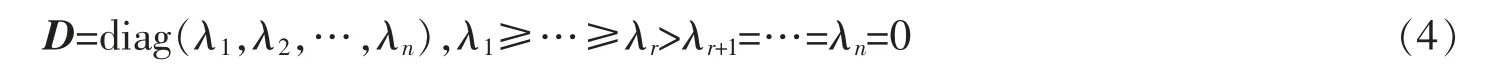
这里r=rank(A)为矩阵A 的秩,λi为A 的特征值,且A 的特征值均非负。 (3)式中矩阵U 的列向量(A 的特征向量)为相应主成分(如U 的第i 个列向量ui为第i 个主成分),D 的对角元λi为相应主成分变量的方差。 每个特征向量为定义主成分的原始变量保存一组回归权重,主成分对应的变量不相关。 下面考虑两种情形:
(1)r=n。 此时在给定分布情形下,随机向量x 的密度函数有定义;
(2)0<r<n。 此时令y=UTx=(y1,y2,…,yn)T,那么有
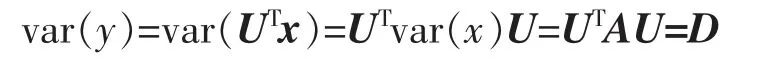
定理1设n 维随机向量x 的协方差矩阵A 有分解(3)式,其中U=[u1,u2,…,un]为正交矩阵,Yk=UkTx,U=[U1,U2],Y1∈Rr,Y2∈Rn-r。 那么有
(1)随机变量y1,y2,…,yr(yi=uiTx)不相关;
(2)对i=1,2,…,r,随机变量yi的方差σi2=λi>0,且σ12≥σ22≥…≥σr2;
(3)对i=r+1,r+2,…,n,有Pr(yi=uiTμ)=1,其中μ 为x 的期望E[x]。
证明注意到

故有

ei∈Rn为第i 个元为1 的坐标向量。因此对i≠j,有cov(yi,yj)=0,从而随机变量y1,y2,…,yr(yi=uiTx)不相关,故结论(1)成立。 对于结论(2),由(5)式,σi2=cov(yi,yi)=λi,又因为λ1≥λ2≥…≥λr>0,所以σ12≥σ22≥…≥σr2,故结论(2)成立。 现证明结论(3):对∀i=r+1,r+2,…,n,有E[yi]=E[uiTx]=uiTE[x]=uiTμ,且由(5)式有cov(yi,yi)=0,所以,yi=uiTμ,即Pr(yi=uiTμ)=1。 证毕。
由定理1 可知,多维随机变量的冗余性可以通过考察其对应的协方差矩阵的奇异性来刻画。 进一步,通过其对应的协方差矩阵的正交对角化找到这样的正交变换,其变换得到的部分变量不相关。
2 正态分布中协方差矩阵的分块
2.1 矩阵正态分布的定义
正态分布是统计学中最基础和最重要的分布。 一元正态分布大约在200 多年前提出,而多元正态分布理论的提出和发展也经历了80 多年。 多元正态分布等价于一个多元随机向量的分布。 1996 年,多变量分析统计专家Kollo T 等人[5]提出了随机矩阵(包括随机向量)的版本。 矩阵版本是向量版本的“双线性”扩展,并且多变量结构从协方差结构获得,该协方差结构将被呈现为两个方差矩阵的Kronecker 积。 然而,另一方面,通过选择特定的协方差结构,总是可以从多元正态分布中获得矩阵正态分布。
多元正态分布至少有三种定义和刻画方法,即利用密度函数、特征函数和通过分布特征(如矩函数等)。文中的方法将依赖于强调正态分布和线性(多线性)变换之间联系的特征,也可以使用其他特征。
众所周知,一元标准正态分布的密度函数定义为

并表示为U~N(0,1)。 由此得出E[U]=0 且D[U]=1。 一般的,若随机变量X 服从均值μ、方差σ2的正态分布,那么变量U=(X-μ)/σ 服从标准正态分布,因此,X 与随机变量

具相同分布,故其密度函数为

记为X~N(μ,σ2),从(7)式可以得出,kX 与kμ+kσU 具有相同的分布。 因此,kX~N(kμ,(kσ)2)。 现在令u=(U1,…,Up)T是一个由p 个独立的同分布(i.i.d.)N(0,1)元素组成的向量。由于独立性,从(6)式可以得到u的密度函数为

记为u~Np(0,I)。
现考虑X 为p 维向量,并记均值E[X]=μ,协方差矩阵为D[X]=Σ,其中Σ 为p 阶半正定矩阵(记Σ≥0)。若Σ>0(正定),则存在满秩阵τ∈Rp×p,Σ=ττT。 不难证明X~Np(μ,Σ)当且仅当X 与下式定义的随机变量具有相同分布

其中u~Np(0,I)。 若Σ>0,则其密度函数为
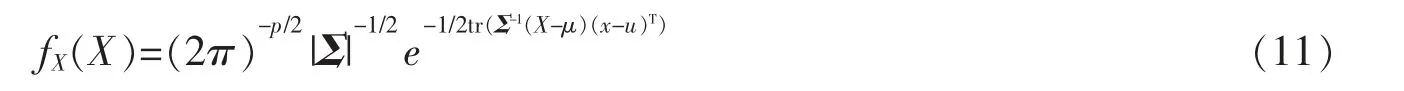
现在引入了矩阵正态分布。
定义1设矩阵X=(Xij)∈Rm×n为随机矩阵,记服从标准正态分布,记X~Nm,n(0,Im,In),若:(1)X·1,X·2,…,X·ni.i.d.Nm(0,Im);(2)X1·,X2·,…,Xm·i.i.d.Nn(0,In)。即X 的行向量和列向量均服从标准正态分布。
定义2令Σ=ττ,Ψ=γγT,其中,τ:p×r,γ:n×s,矩阵X:p×n 被称为关于参数(μ,Σ,Ψ)的矩阵正态分布,如果它和下式定义的随机矩阵有相同的分布

其中μ:p×n 是非随机常数矩阵,U:r×s 是s 由个i.i.d.于Nr(0,I)的向量Ui(i=1,2,…,s)组成。 如果X:p×n 是矩阵正态分布,则将其表示为X~Np,n(μ,Σ,Ψ)。 如果Σ,Ψ 是正定的,则(12)式中的τ 和γ 均是非奇异矩阵。以下讨论排除情况Σ=0,Ψ=0。
推论1若X=(Xij)∈Rm×n,且X~Np,n(μ,Σ,Ψ),则有
(1)X·1,X·2,…,X·ni.i.d.Nm(μ·j,ΨjjΣ);(2)X1·,X2·,…,Xm·i.i.d.Nn(μi·,ΣiiΨ)。
定理2令X~Np,n(μ,Σ,Ψ),对任意的A:q×p 和B:m×n,有
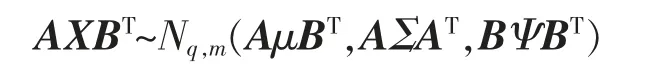
定理3X~Nm,n(0,Im,In)当且仅当vecX~Nmn(0,Imn)。
证明令,其中,X·j=(X1j,X2j,…,Xmj)T,j=1,2,…,n
所以

X~Nm,n(0,Im,In)当且仅当vecX~Nmn(0,Imn)。
推论2X~Np,n(μ,Σ,Ψ)当且仅当vecX~Npn(vecμ,Ψ⊗Σ)。
性质1若X~Np,n(μ,Σ,Ψ),则vecX 密度函数为
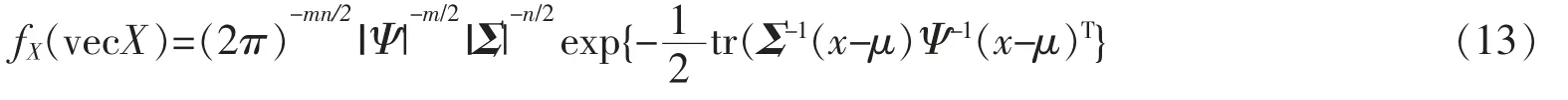
证明令x=vecX。 因若X~Np,n(μ,Σ,Ψ),则vecX~Npn(vecμ,Ψ⊗Σ),因此,由式(11)知

又因为vec(AXB)=(BT⊗A)vecX,且tr(AB)=tr(BA),所以
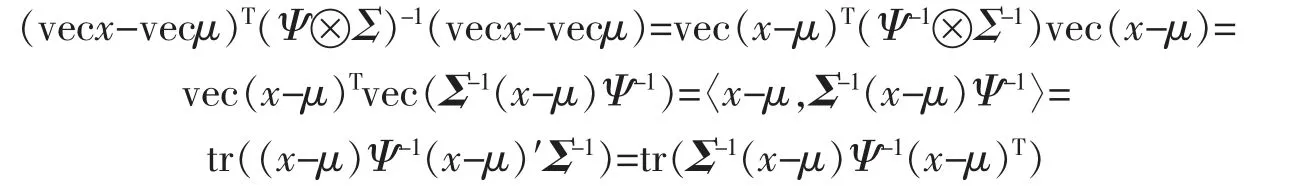
又因为|Ψ⊗Σ|=|Ψ|m|Σ|n,所以
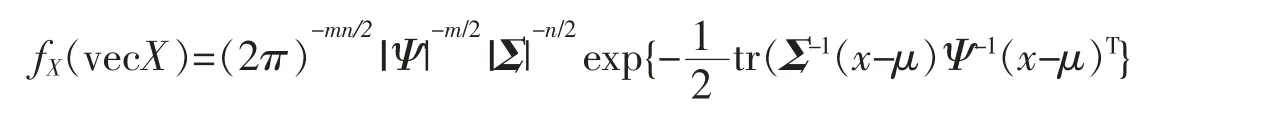
推论3若X~Nm,n(0,Im,In),则vecX 的密度函数为

2.2 矩阵正态分布的一些性质
当协方差矩阵为奇异矩阵时,原始随机变量之间一定存在相关性,这时随机变量存在冗余,需要考虑协方差矩阵的分块,希望剔除相关变量,并找出不相关随机变量。
考虑若X=(Xij)∈Rm×n的分块,使用以下记号

推论4令X~Np,n(μ,Σ,Ψ),其中X,μ,Σ 和Ψ 如(15-19)式所定义,那么
(1)X11~Nr,s(μ11,Σ11,Ψ11);(2)X12~Nr,n-s(μ12,Σ11,Ψ22);(3)X21~Np-r,s(μ21,Σ22,Ψ11);(4)X22~Np-r,n-s(μ22,Σ22,Ψ22);(5)X·1~Np,s(μ·1,Σ,Ψ11);(6)X·2~Np,n-s(μ·2,Σ,Ψ22);(7)X1·~Nr,n(μ1·,Σ11,Ψ);(8)X2·~Np-r,n(μ2·,Σ22,Ψ)。
证明(1)令A=(Ir,0),则
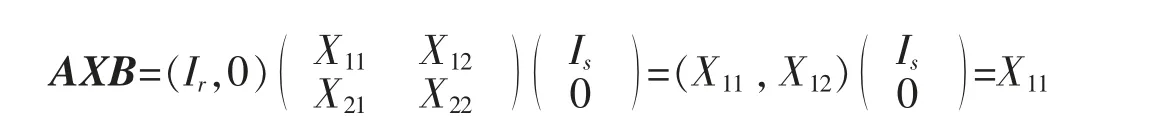
由定理2 知AμB=μ11,AΣAT=Σ11,BTΨB=Ψ11,因此,
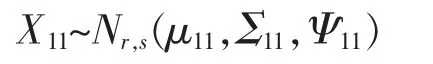
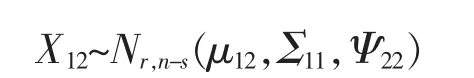
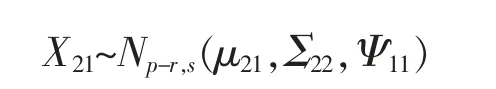
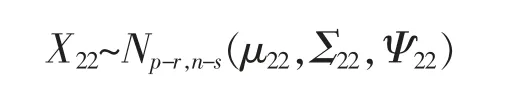
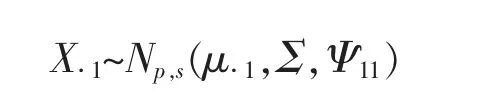
同理可证(6)、(7)、(8)。
推论4 说明:一个服从矩阵正态分布的随机矩阵,其对应的每个列(行)随机向量、子矩阵也服从矩阵正态分布。 下面将进一步证明:服从矩阵正态分布的随机矩阵,其对应的分块条件分布也服从矩阵正态分布。
3 条件正态分布协方差矩阵的分块
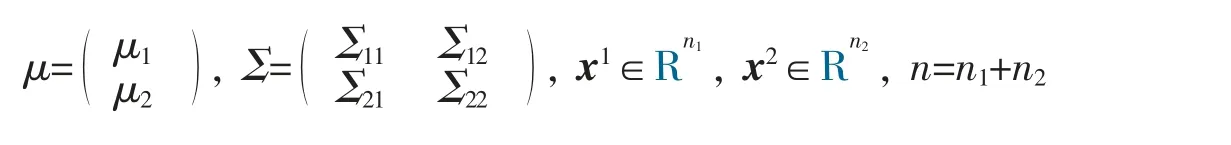
这里仍采用(15-19)式中的记号,那么有
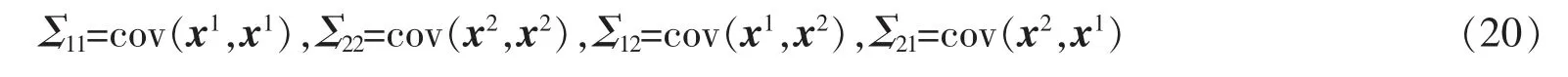
且

下面来研究随机向量x1与x2的相关性。 有结论:
定理4[6]若Σ22非奇异,则x1|x2~Nn1(μ1.2,Σ11.2), 其中
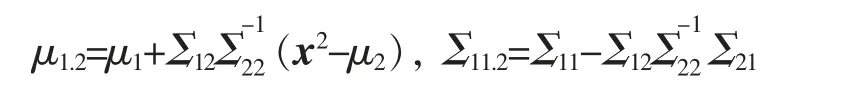
Σ11.2称为Σ 关于Σ22的Schur 补。
证明令
由性质知Ax~Nn(Aμ,AΣAT),将代入得
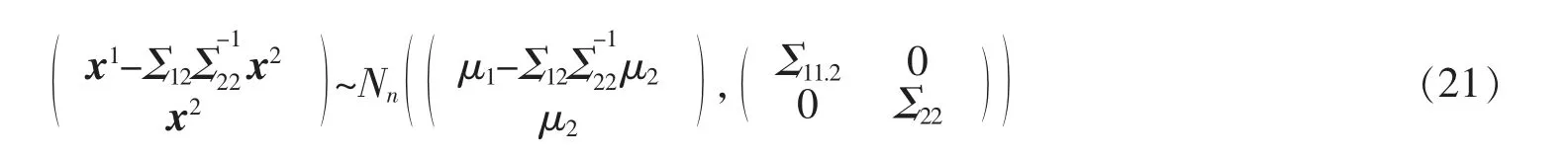
由上式可得x1-Bx2╧x2。 所以有

其中

假设Σ11是非奇异的并注意到任何C,有
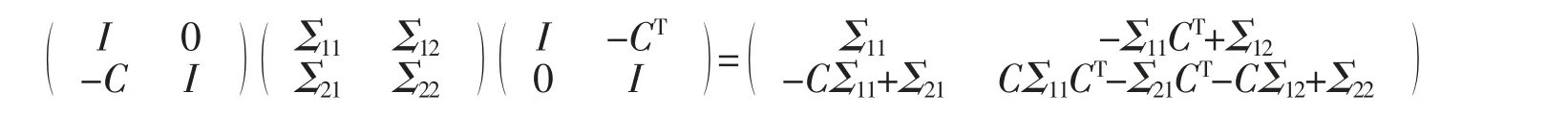
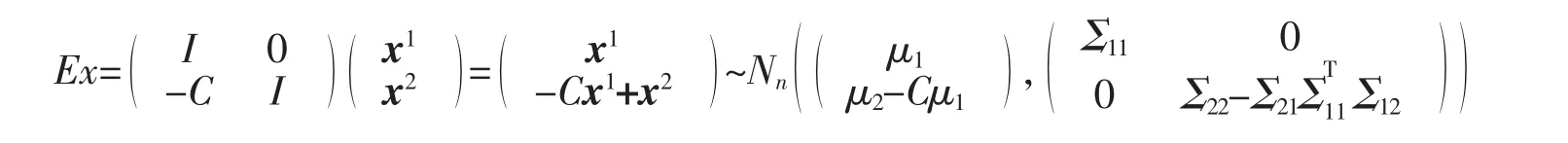
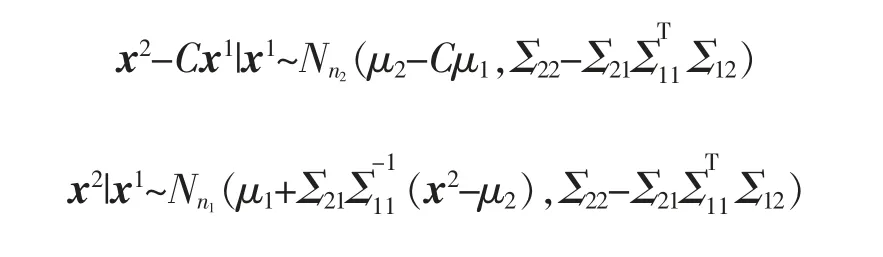
假设Σ22是奇异的,则存在正交矩阵和非奇异矩阵D,使得
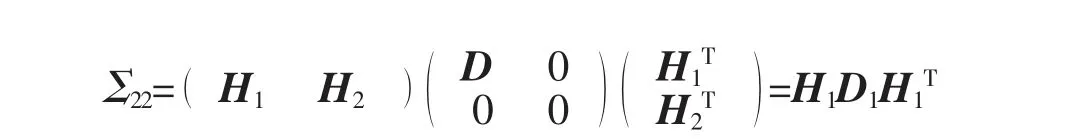
那么
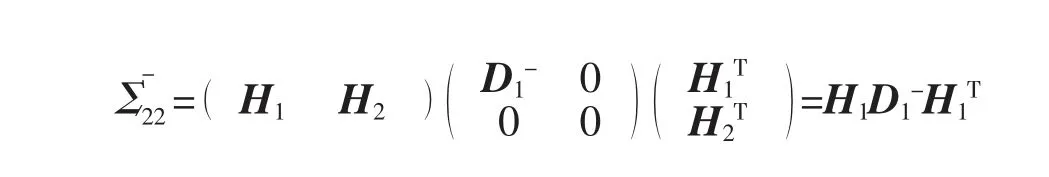
又x2~Nn(μ2,Σ22)⇒x2-μ2~Nn(0,Σ22),H2T(x2-μ2)~Nn(0,H2TΣ22H2)。
因为H 为正交矩阵,所以

因此,H1TH1=In1,H2TH2=In2,H1TH2=H2TH1=0,所以

因此,可以得到


由定理4 可知:服从矩阵正态分布的随机矩阵,其对应的分块条件分布也服从矩阵正态分布。
4 奇异协方差矩阵对应的线性回归模型
给定随机向量x=(x1,x2,…,xn)T∈Rn对应的协方差阵Σ。若Σ 可逆,则在给定x 服从某分布的条件下,其对应的分布密度函数可以经其分布参数(μ,Σ)表示。 但在Σ 奇异的条件下,其对应的密度函数无法表示,该节讨论Σ 奇异时对应的密度函数[7-12]。
设x~N(μ,Σ),则存在正交矩阵U,使得Σ=UDUT,其中D=diag(λ1,…,λn)。
若λ1≥λ2≥…≥λn>0,即Σ 正定(Σ 可逆),则有
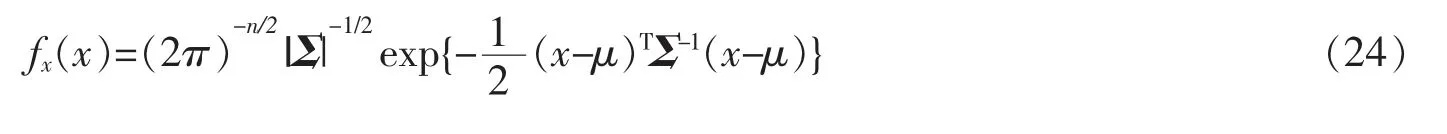
更一般的,有
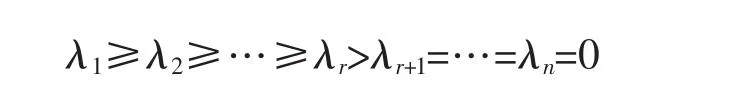
即Σ 奇异,rank(Σ)=r (1)广义逆来代替逆。 用Σ+表示Σ 的广义逆,则 其中U1=(u1,…,ur)∈Rn×r,因此 (2)因为Σ=UDUT,所以其中,D1=diag(λ1,…,λr)。 令y=UTx=(y1,y2,…,yn)T,则 所以∀i=1,…,r,有σ2(yi)=λi;∀i=r+1,…,n,有σ2(yi)=0。 因此,y1,y2,…,yr为两两互相独立的随机变量,yr+1,…,yn为常量。 令Y1=(y1,y2,…,yr) 该节将给出几个实例,以说明协方差矩阵在多元线性回归模型刻画及其参数估计中的应用。 例1假设随机向量x∈Rm的均值为μ,方差为Ω,且Ω 为正定的,这时可以定义一个关于x 的线性变换,使得变换后的随机向量是标准的,即它的均值为0,协方差矩阵为Im。 令Ω1/2是任意的满足Ω=Ω1/2(Ω1/2)T的矩阵,并令z=Ω-1/2(x-μ),其中Ω-1/2=(Ω1/2)-1,可以发现 和 例2对于一个多元线性回归模型 其中y=(y1,y2,…,yN)T∈RN,X∈RN×r, β=(β1,β2,…,βN)T∈RN, ε=(ε1,ε2,…,εN)T∈RN,并且ε~NN(0,σ2In),用来表示对参数β 的一个估计,则则 对f(β)关于β 求导得f′(β)=2(XTX)β-2XTy,令f′(β)=0,得到(XTX)β=XTy,因此,可以推出=(XTX)-1XTy。 当ε~NN(0,σ2C)时,其中C=diag(c12,c22,…,cN2)为一个对角矩阵,ci是常数,则 现在,定义一个新的线性模型 等效地y*=X*β+ε*,其中 那么ε*的协方差矩阵为 参数β 的估计值为 例3在例2 中得到了在多元回归规模型y=Xβ+ε 中对β 的一个加权最小二乘估计,现在考虑广义最小二乘估计。 当ε~NN(0,σ2C)时,其中C∈RN×N是一个已知的正定矩阵,现在想要得到一个使得随机误差的协方差为σ2In的变换,可令T∈RN×N为满足TTT=C 的矩阵,定义一个新的多元线性模型 等效地y*=X*β+ε*,其中y*=T-1y,X*=T-1X,ε*=T-1ε,那么ε*的协方差矩阵为 因此,参数β 的估计值为 笔者主要研究了矩阵分块方法在协方差矩阵中的应用。 首先,论文介绍了协方差矩阵的基本性质及正态分布随机变量的协方差矩阵的分块特征;然后,通过矩阵分块方法,结合矩阵分解和矩阵广义逆,介绍了奇异协方差矩阵对应的线性回归模型和矩阵分块方法在多元线性回归中的应用。
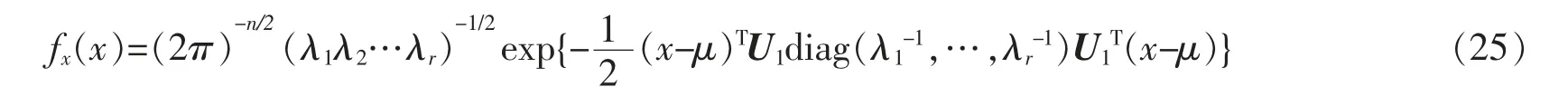
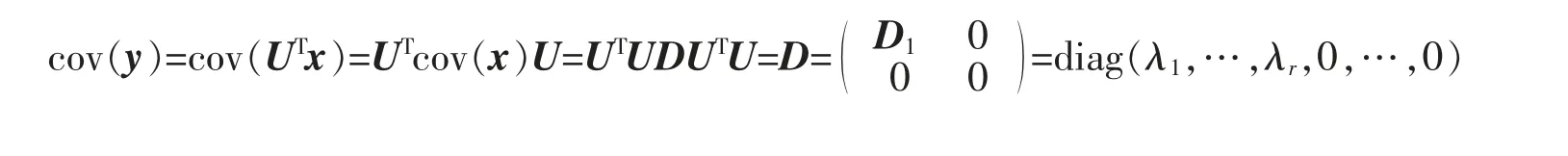

5 协方差矩阵在多元线性回归中的应用
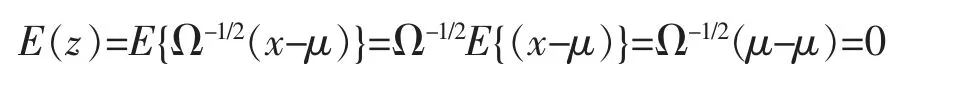

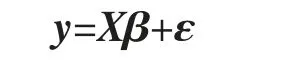
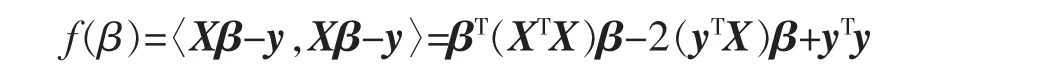
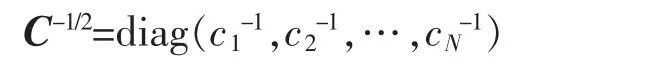
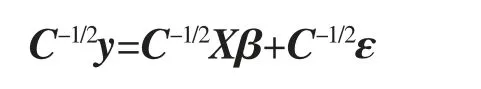

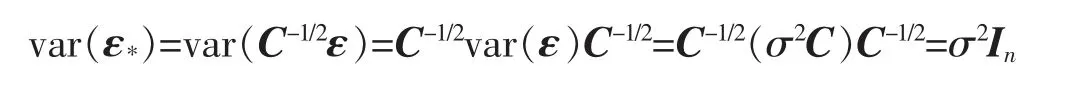
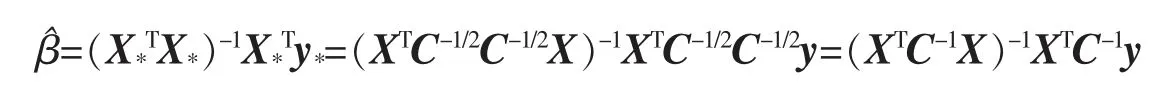
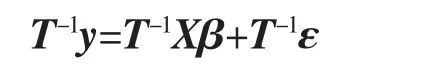
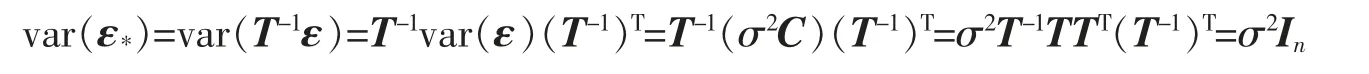
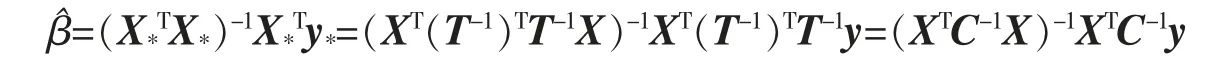
6 结语

