Precise large deviations of aggregate claims in a size-dependent and delayed risk model with WOD claims

XUN Baoyin， WANG Kaiyong

（School of Mathematical Sciences，SUST，Suzhou 215009，China）

Abstract： This paper considers a size-dependent risk model.In this model there exists a dependence structure between the claim sizes and the inter-arrival times.When the claim sizes have a widely orthant dependent structure and the number process of claims is a delayed renewal counting process，the precise large deviations of aggregate claims have been obtained for the heavy-tailed claim sizes.

Key words： precise large deviations；size-dependent risk model；aggregate claims；heavy-tailed distributions

1 Introduction

1.1 Risk model

In this paper we will consider the following risk model.Assume that the claim sizes，Xi，i≥1 form a sequence of identically distributed and nonnegative random variables （r.v.s） with common distribution F and finite mean μ＞0.There will exist a dependence structure among the claim sizes.The inter-arrival times，θi，i≥1 are a sequence of nonnegative and independent r.v.s.Let m be a positive integer.Assume that θi，i＞m are identically distributed with common distribution G and finite mean λ-1＞0 and θi，1≤i≤m，have distributions Gi，1≤i≤m，which are not necessary identically distributed.Assume that（Xi，θi），i＞m form a sequence of identically distributed copies of a generic random pair （X，θ）.We denote the arrival times of the claim sizes bywhich constitute a delayed renewal counting process

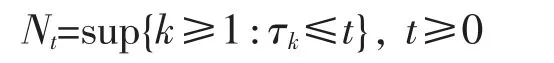
and it has a finite mean function λ（t）=E[Nt]→∞as t→∞.Thus，the aggregate amount of claims is a random sum of the form

In this paper，we will investigate the precise large deviations of the random sum St，t≥0.That is to say，we will mainly discuss the asymptotics of P（St-μλ（t）＞x） as t tends to ∞，which holds uniformly for x≥γλ（t），γ＞0.

For the precise large deviations of random sums and their applications in insurance，when θi，i≥1 are identically distributed and X is independent of θ，there are many researchers to study this case，such as Cline and Hsing[1]，Heyde[2]，Nagaev[3]，Ng et al[4]，Chen[5]，Gao et al[6]，Chen et al[7]and so on.Recently，Chen et al[8]considered a dependent case，where there exists a dependence structure between the claim sizes Xiand their corresponding inter-arrival times θi，i≥1.In this paper，we still consider this dependence structure.In the insurance business，claims are often influenced by common factors.This paper will consider the claims are dependent.We mainly consider the widely orthant dependent structure.Meanwhile，this paper will investigate the case that the number process of claims is a multi-delayed counting process.For the review and significance of the risk model with a multi-delayed counting process，one can see Gao and Wang[9].

1.2 Preliminaries and main results

Throughout this paper，all limit relations are for t→∞，unless stated otherwise.For a real number y，denote its integer part by [y].For a nonnegative function g（x），if there exists a constant a＞0 such that g（x）≤ag（y） for all 0≤y＜x＜∞，then write g（x）↓.For two positive functions a（t） and b（t），if lim sup a（t）/b（t）≤1 then write a（t）≾b（t）；if lim inf a（t）/b（t）≥1 then write a（t）≿b（t）；if lim a（t）/b（t）=0 then write a（t）=o（b（t））；if lim sup a（t）/b（t）＜∞then write a（t）=O（b（t））.Furthermore，for two bivariate functions a（x，t） and b（x，t），we write a（x，t）～b（x，t） uniformly for all x from some nonempty set Δ as t→∞，if

write a（x，t）≾b（x，t） uniformly for all x∈Δ as t→∞，if

and write a（x，t）≿b（x，t） uniformly for all x∈Δ as t→∞，if

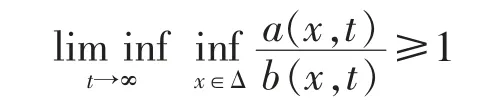
For a distribution V on （-∞，∞），if（dy）=∞for any λ＞0，then we say that V is a heavy-tailed distribution.For a distribution V on （-∞，∞），say that V belongs to the dominated varying tail distribution class，denoted by V∈D，if for any 0＜y＜1，

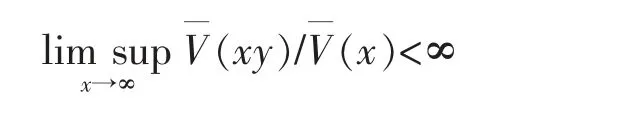
The class D is associated with the Matuszewska index below.For a distribution V on （-∞，∞），denote its upper and lower Matuszewska indices，respectively，by

（i）V∈D；（ii）JV+＜∞；（iii）LV＞0.

（see，e.g.Bingham et al[10]or Proposition 1.1 of Wang et al[11]）.

Definition 1For the r.v.s {ξn，n≥1}，if there exists a finite real sequence {gU（n），n≥1} satisfying，for each integer n≥1 and for all xi∈（-∞，∞），1≤i≤n，

then we say that the r.v.s {ξn，n≥1} are widely upper orthant dependent （WUOD） with dominating coefficients gU（n），n ≥1；if there exists a finite real sequence {gL（n），n ≥1} satisfying，for each integer n ≥1 and for all xi∈（-∞，∞），1≤i≤n，

then we say that the r.v.s {ξn，n≥1} are widely lower orthant dependent （WLOD） with dominating coefficients gL（n），n≥1；if they are both WUOD and WLOD，then we say that the r.v.s {ξn，n≥1} are widely orthant dependent （WOD）.

The above dependence structures are introduced by Wang et al[12]，which shows the wide dependence structures can contain some common dependence structures including the negatively upper/lower orthant dependence（NUOD/NLOD） （see Ebrahimi and Ghosh[13]and Block et al[14]） and the extendedly negatively orthant dependence （ENOD） （see Liu[15]and Chen et al[16]）.

Assumption 1Assume that there exists a dependence structure between X and θ.There is a nonnegative random variable θ*such that θ conditional on {X＞x}，is a stochastically bounded by θ*for all large x＞0；in other words，there is some x0＞0 such that it holds for all x＞x0and t∈[0，∞） that

Now we introduce a nonnegative random variablethat is independent of all sources of randomness and is identically distributed as θ conditional on {X＞x}.Correspondingly，denote

and define

Note that {Nt*，t≥0} is a delayed renewal counting process.Note also the distribution ofdepends on x through the condition {X＞x}，so does the distribution of {Nt*，t≥0}.

The following is the main result of this paper.

Theorem 1Consider the aggregate amount of claims （1）.Suppose that Assumption 1 is satisfied and Xi，i≥1 are WOD r.v.s with dominating coefficients gU（n），n≥1 and gL（n），n≥1 satisfying for any α∈（0，1），

Suppose that there exists a nondecreasing and positive function g（x），x≥0 and some constant 0＜k＜1 such that

If F∈D，then for any fixed γ＞0，it holds uniformly for all x≥γλ（t） that

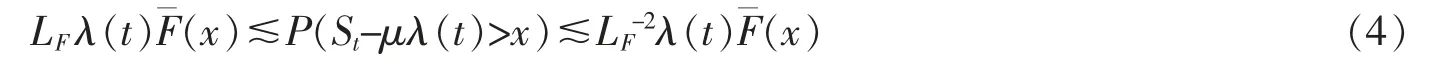
Remark 1（i）Note that the condition （3） is only needed when we use the strong large number law for WOD r.v.s，which is Lemma 3 below.

（ii）If the claim sizes Xi，i≥1 are ENOD r.v.s，then the conditions （2） and （3） are satisfied.We can obtain the following corollary directly from Theorem 1.

Corollary 1Consider the aggregate amount of claims （1）.Suppose that Assumption 1 is satisfied and Xi，i≥1 are ENOD r.v.s.If F∈D then for any fixed γ＞0，（4） holds uniformly for x≥γλ（t）.Especially，if F∈C then for any fixed γ＞0，it holds uniformly for all x≥γλ（t） that

In the following we will first give some lemmas in Section 2.The proof of the main result will be present in Section 3.

2 Some lemmas

In order to prove Theorem 1，we will give some lemmas.The first lemma is from Proposition 2.2.1 of [10]and Lemma 3.5 of Tang and Tsitsiashvili[17].

Lemma 1Let V be a distribution on （-∞，∞） belonging to the class D.

（i）For any β＞JV+there exist two positive constants c and d such that when x≥y≥d，

（ii）For any β＞JV+，x-β=o（V（x）） as x→∞.

The following lemma extends Lemma 2.1 of [8] to the renewal counting process with m+1 delays.

Lemma 2Suppose that Assumption 1 is satisfied.Then it holds for every 0 ＜δ ＜1 and every function γ（·）:[0，∞）|→（0，∞） with γ（t）↑∞as that

ProofFor all large t， it holds that

By Proposition 3.5.1 of Ross[18]，we have λ（t）～λt.Then by the strong large number law for independent and identically distributed r.v.s，it holds that

Thus，we have

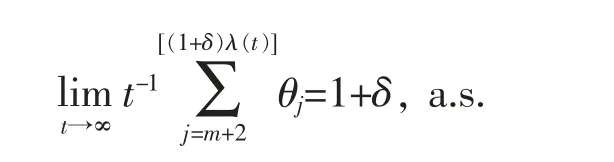
Similarly，we can obtain that

Thus，it holds that

and

Since for all t＞0，

By （8），we have

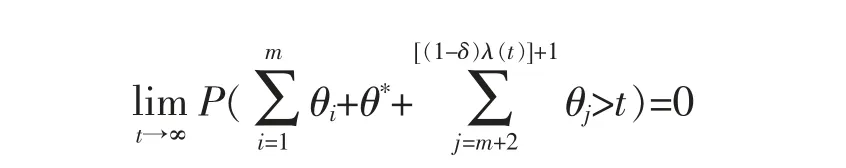
which combining with （6） and （7） yields that （5） holds.

The following lemma comes from Theorem 1.4 of Wang et al[19].

Lemma 3Assume that ξi，i≥1 are WOD r.v.s with dominating coefficients gU（n），n≥1 and gL（n），n≥1，common distribution V on（-∞，∞） and finite mean.Suppose that there exists a nondecreasing and positive function g（x），x≥0 and some constant 0＜k＜1 such that E｜ξ1｜g（｜ξ1｜）＜∞，x-kg（x）↓and max{gU（n），gL（n）}≤g（n），n≥1.Then

Lemma 4 is from Theorem 2.2 of Gao et al[20].

Lemma 4Let ξi，i≥1 be a sequence of nonnegative and WUOD r.v.s with dominating coefficients gU（n），n≥1，common distribution V∈D and finite mean.Assume thatfor any α∈（0，1）.Then，for any fixed γ＞0，it holds that

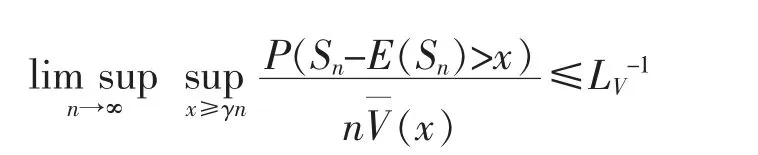
The following lemma extends Lemma 2.3 of [8] to the delayed case.

Lemma 5Under the conditions of Theorem 1，it holds that for every p＞JF+，there is some constant C＞0 such that，uniformly for all x≥0，t≥0 and 1≤n≤m，

and uniformly for all x≥0，t≥0 and n＞m，

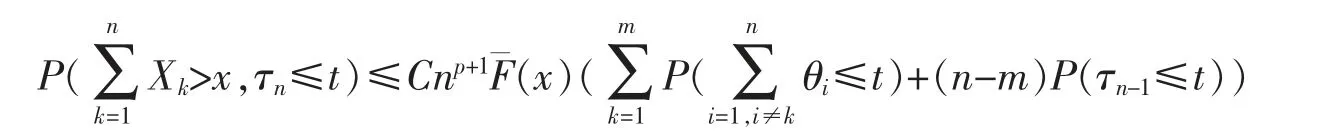
ProofFor all x≥0，t≥0 and n≥1，

When 1≤n≤m，by （10），it holds for all x≥0，t≥0 and 1≤n≤m that

When n＞m，since θi，i≥1 are independent and θi，i＞m are identically distributed，it holds for all x≥0，t≥0 and n＞m that

Since F∈D，by Lemma 1，for any fixed p＞JF+，there exist positive constants C1and x0such that for all x≥nx0，

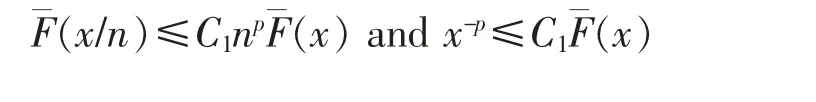
Hence，

where C=C1x0p+C1，which combining with （11） and （12） obtains the results of Lemma 5.

The following lemma gives a delayed version of Theorem 1（i） ofet al[21].

Lemma 6Under the conditions of Theorem 1，then，it holds for every a＞λ and some b＞1 that

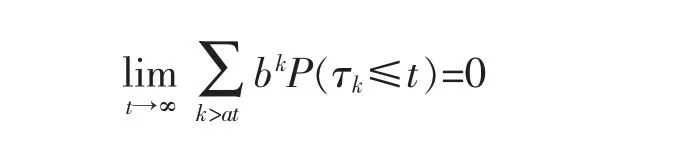
ProofDenoteFor any y＞0 and sufficiently large t，by Markov’s inequality，we have that

where h（y）=Ee-yθandSince h（y）＜1 for any y＞0，there exists a constantsuch that bh（y）＜1.

By （13），it holds for sufficiently large t that，

By the proof of Theorem 1 of [21]，we get that there exists a constant y*＞0 such that

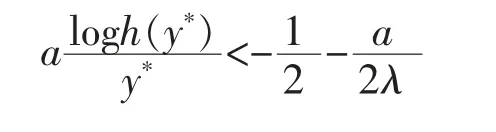
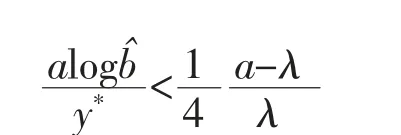
Therefore，for sufficiently large t and some positive constant y*，

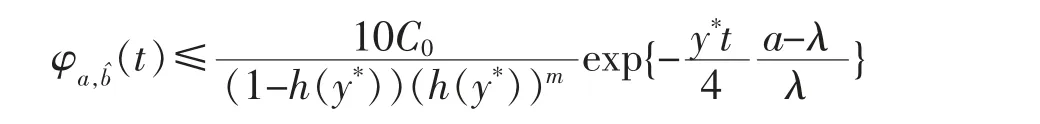
Letting t→∞in the above equation，the result of this lemma can be obtained.

3 Proof of Theorem 1

In order to prove （4），it is sufficient to prove that for any fixed γ＞0，

and

We first prove （14）.For any fixed 0＜δ＜1，it holds for any x＞0 and t＞0 that

For J1（x，t），taking δ such that γ-μδ＞0.For any 0＜γ1＜（γ-μδ）/（1+δ），since x≥γλ（t），it holds that

Hence，by Lemma 4，it holds uniformly for x≥γλ（t） that

Next，we deal with J2（x，t）.By Lemmas 5 and 6，for every p＞JF+it holds uniformly for x≥γλ（t） that

Since λ（t）～λt，for any 1/（1+δ）＜a＜1，it holds for sufficiently large t that λ（t）≥aλt.

Then it holds uniformly for x≥γλ（t） that

By （17），（18） and F∈D，it holds that

Next，we prove（15）.Let 0＜δ＜1 and v＞1，by the proof of Theorem 1.1 of Chen and Yuen[8]，it holds uniformly for x≥γλ（t） that

Firstly，we deal with the sum of I1（x，t，n）.By the definition of Nt*，t≥0，it holds uniformly for x≥γλ（t） that

Hence，it holds uniformly for x≥γλ（t） that

Letting δ be small enough such that μδ+（1-v）γ＜0.By Lemma 3，it holds uniformly for x≥γλ（t） that

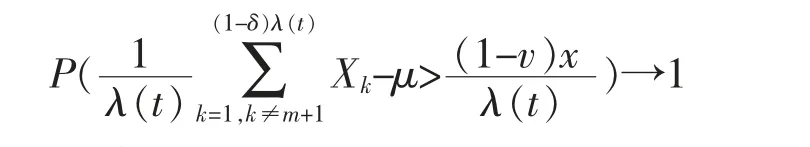
By Lemma 2，it holds uniformly for x≥γλ（t） that

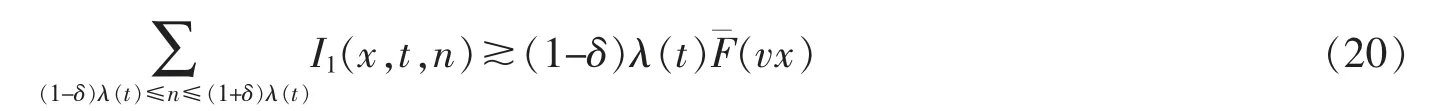
Next，we deal with I2（x，t，n）.Since Xi，i≥1 are WOD，we have

holds uniformly for x≥γλ（t）.

Hence，by F∈D，

By （19）-（21），

This completes the proof of Theorem 1.