覆盖Gorenstein AC-平坦维数

陈 东, 胡 葵

(1. 成都大学 信息科学与工程学院, 四川 成都 610106； 2. 西南科技大学 理学院, 四川 绵阳 621010)

近年来, 许多学者研究了Gorenstein平坦模类的扩张封闭性。2009年，Bennis[1]称Gorenstein平坦模类关于扩张封闭的环为GF-闭环，同时证明了若R是GF-闭环，则Gorenstein平坦模类是投射可解的。特别地，凝聚环、弱整体维数有限的环类都是GF-闭环。2015年，Bouchiba[2]引入了模的覆盖Gorenstein平坦维数，证明了对任意R-模M，若M的覆盖Gorenstein平坦维数等于Gorenstein平坦维数，则R也是GF-闭环。

作为GF-闭环的应用，文献[3]研究了Gorenstein-平坦模类的稳定性，证明了GF-闭环上Gorenstein-平坦模类都具有稳定性。用GF2(R)(或GF(2)(R)) 表示满足以下条件的模M构成的类，如果存在Gorenstein-平坦模Gi、Gi的正合列

…→G1→G0→G0→G1→…

使得M≅Ker(G0→G0)，且对每个Gorenstein内射模 (或内射模)I，函子I⊗-使上述正合列保持正合。若上述模类满足：GF(R)=GF2(R)=GF(2)(R),则称Gorenstein-平坦模类是稳定的。

2018年，Bravo等[4]引入了GorensteinAC-平坦模。称R-模M为GorensteinAC-坦模，若存在平坦模Fi、Fi的正合列

…→F1→F0→F0→F1→…

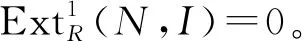
受以上思想启发，本文定义了模的覆盖GorensteinAC-平坦维数，讨论了覆盖GorensteinAC-平坦维数与余纯平坦维数、GorensteinAC-平坦维数和平坦维数之间的关系，给出了覆盖GorensteinAC-平坦维数等于GorensteinAC-坦维数的一个充分条件，由此证明了在此条件下GorensteinAC-平坦模类关于扩张封闭(投射可解)，进而GorensteinAC-平坦模类具有稳定性，完善了文献[4]中对GorensteinAC-平坦模性质的讨论。值得注意的是，文献[14]证明了若R是GFAC闭环，则GorensteinAC-平坦模类具有稳定性，但没有给出具体的环类。本文给出GFAC闭环的一个充分条件，并给出GFAC闭环一些具体的环类 (如弱整体维数有限环)。

设H是R- 模类，称H是投射可解类，如果投射模包含在H中，并且对任意X′∈H的正合列0→X″→X→X′→0，X″∈H当且仅当X∈H。

为便于讨论，本文所涉及的环均是有单位元的交换结合环，所涉及的模均是酉模。用GF(R)表示Gorenstein-平坦模类，GFAC(R) 表示GorensteinAC-平坦模类。

1 预备知识

文献[15]引入了GorensteinAC-内射维数，称为Gorenstein弱内射维数。R-模M的GorensteinAC-内射维数定义为：GAC-idRM=inf{n∈N|存在正合列0→M→G0…→Gn-1→Gn→0，其中Gi(0≤i≤n)是GorensteinAC-平坦模}。相应地，如下定义R-模M的GorensteinAC-平坦维数。

定义1设M是R-模，M的GorensteinAC-平坦维数定义为

GAC-fdRM=inf{n∈N| 存在正合列0→Fn→Fn-1…→F0→M→0，其中Fi(0≤i≤n)是GorensteinAC-平坦模}。

由定义，当GAC-fdRM=0 时，M是GorensteinAC-平坦模；当GAC-idRM=0 时，M是GorensteinAC-内射模。容易看到，{平坦模}⊆{GorensteinAC-平坦模}⊆{Gorenstein平坦模}，即GorensteinAC-平坦模类是介于平坦模类和Gorenstein平坦模类之间的一种模类。

现定义模M的覆盖GorensteinAC-平坦维数。

定义2设M是R-模，n是非负整数，R-模M的覆盖GorensteinAC-平坦维数定义为CGAC-fdRM=inf{n| 存在R-模的正合列0→M→F→G→0，其中fdRF=n，G是GorensteinAC-平坦模}。如果上述集合为空集，则规定CGAC-fdRM=∞。

命题1设M是GorensteinAC-坦模，则M+是GorensteinAC-内射模；若R是凝聚环，则反之也成立。

证明设M是GorensteinAC-平坦模，则存在平坦模Fi、Fi的正合列

F=…→F1→F0→F0→F1→…

使得M≅Ker(F0→F0)，且对任意绝对纯模I，I⊗F是正合的。于是又有

(I⊗F)+=…→(I⊗F1)+→(I⊗F0)+→(I⊗F0)+→(I⊗F1)+→…

是正合的。由于(Fi)+、(Fi)+是内射模，从而有

F+=…→(F1)+→(F0)+→(F0)+→(F1)+→…

是内射模的正合列，且M+≅Ker((F0)+→(F0)+)。另一方面，由相伴同构定理，有

…→HomR(I,(F1)+)→HomR(I,(F0)+)→HomR(I,(F0)+)→HomR(I,(F1)+)→…

是正合的。因此，M+是GorensteinAC-内射模。

反之，设M+是GorensteinAC-内射模，从而也是Gorenstein内射模。由于R是凝聚环，由文献[16]定理3.6知，M是GorensteinAC-平坦模。证毕。

2 主要结果及证明

命题2①设M是R-模，则cfdRM≤G-idRM+≤GAC-idRM+≤GAC-fdRM≤CGAC-fdRM≤fdRM;

②若CGAC-fdRM<∞，则cfdRM=G-idRM+=GAC-idRM+=GAC-fdRM=CGAC-fdRM。

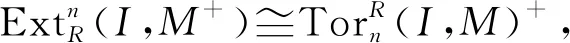
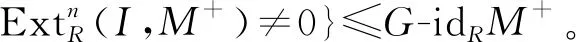
由于GorensteinAC-内射模类是Gorenstein内射模类，因此，又有:G-idRM+≤GAC-idRM+。另一方面，由命题1知，若M是GorensteinAC-平坦模，则M+是GorensteinAC-内射模，故又有GAC-idRM+≤GAC-fdRM。

现设CGAC-fdRM=n，由定义2知，存在正合列0→M→F→G→0, 其中fdRF=n，G是GorensteinAC-平坦模。考虑以下行为正合列的交换图

其中第1列和第3列分别是M和G的部分投射分解，Pi和P′i(0≤i≤n-1) 是投射模。由文献[4]中引理4.4(3) 知，G′是GorensteinAC-平坦模。由于fdRF=n，故F′ 是平坦模。对第1行正合列，由于G′是GorensteinAC-平坦模，F′是平坦模，故由文献[4]中引理 4.4(3)知，M′是GorensteinAC-平坦模，于是，由第1列知，GAC-fdRM≤n。

若设fdRM=n。考虑正合列0→M→M→0, 由定义2知，CGAC-fdRM≤fdRM。

对于一般环，无法证明GorensteinAC-平坦模类关于扩张封闭，但可以证明存在如下关系。

命题3设0→A→B→C→0 是正合列，若A、C是GorensteinAC-平坦模，则GAC-fdRB≤1。

证明由于C是GorensteinAC-平坦模，由文献[4]中定义4.1知，存在正合列0→G→F→C→0, 其中F是平坦模，G是GorensteinAC-平坦模。考虑以下正合列的交换图

由于A是GorensteinAC-平坦模，由文献[4]中引理4.4知，存在正合列：0→A→P→H→0,其中P是平坦模，H是GorensteinAC-平坦模。于是，又有以下正合列的交换图

对正合列0→P→L→F→0，由于P、F是平坦模，故L也是平坦模。由文献[4]中引理4.4知G′是GorensteinAC-平坦模。于是，对正合列0→G→G′→B→0, 由于G、G′是GorensteinAC-平坦模，故GAC-fdRB≤1。证毕。

文献[1]称Gorenstein平坦模类封闭的环为GF-闭环，文献[2]引入覆盖Gorenstein平坦维数，给出了GF-闭环的一个充分条件。本文称GorensteinAC-平坦模类封闭的环为GFAC-闭环，同时用覆盖Gorenstein平坦维数，给出环R是GFAC-闭环的一个充分条件。

定理1设R是环，若对任意R-模M，都有CGAC-fdRM=GAC-fdRM，则R是GFAC-闭环。

证明设0→A→B→C→0 是正合列，其中A、C是GorensteinAC-平坦模。由命题3知，GAC-fdRB≤1<∞。故由命题2知，GAC-idRB+=GAC-fdRB。另一方面，又存在正合列0→C+→B+→A+→0，其中A+、C+是GorensteinAC-内射模，故由文献[15]中命题2.11知B+也是GorensteinAC-内射模，因此，由上述关系有GAC-idRB+=GAC-fdRB=0，从而B是GorensteinAC-平坦模。证毕。

…→G1→G0→G0→G1→…

由定理1，容易得到以下2个推论。

推论1[4]设R是环，若对任意R-模M，都有CGAC-fdRM=GAC-fdRM，则GorensteinAC-平坦模类关于正向极限封闭，此时，每个R-模有GorensteinAC-平坦盖。

推论2[4]设R是环，若对任意R-模M，都有CGAC-fdRM=GAC-fdRM，则 (GFAC(R),GFAC(R)⊥)是完备的遗传余挠理论。

定理2[3]若R是GFAC-闭环，则GorensteinAC-平坦模类是稳定的。

由定理2，容易得到以下推论3。

推论3[14]设R是环，若对任意R-模M，均有CGAC-fdRM=GAC-fdRM，则GorensteinAC-平坦模类是稳定的。

当R是凝聚环时，{GorensteinAC-平坦模}={Gorenstein平坦模}，此时R是GF-闭环，因而有：设R是凝聚环，则GorensteinAC-平坦模类是稳定的。此结论是文献[3]的一个结果。

由命题2，对任意R-模M，若fdRM<∞，则GAC-fdRM=CGAC-fdRM，故R是GF-闭环。于是又有：设R是环，且w.gl.dim(R)<∞，则GorensteinAC-平坦模类是稳定的。