带线性项Kirchhoff型问题的无穷多古典解
王 跃, 叶红艳, 雷 俊, 索洪敏*
(1. 贵州大学 数学与统计学院, 贵州 贵阳 550025; 2. 贵州民族大学 数据科学与信息工程学院, 贵州 贵阳 550025)
早在1876年以前,德国物理学家Kirchhoff[1]便提出了经典的波动方程
式中ρ、h、p0、E、L均为正数,0 解的存在性。2015年以来,该问题在国内外受到广大数学爱好者的关注并有大量研究成果[2-12]。特别地,文献[2]中罗列了大量关于上述问题的研究结果,此处不再赘述。文献[3]首次指出这类问题从某种角度可以视为负模量的Kirchhoff型问题,从而表明这类问题的研究具有一定的价值。 考虑含负模量的非局部Kirchhoff型问题古典解的存在性 (1) 式中:Ω⊂RN(N≥1)是光滑有界域;a、b、λ为任意实数(常数参数都可以);u=u或是边界∂Ω上的单位外法向量。文献[4]通过变分方法获得当N≥3,u=u,并且a、b、λ为3个正参数时,该问题至少存在一正一负2个弱解,并利用反证法说明λ较小时不存在同号解。值得一提的是, 文献[2-12]及其引用的关于负模量问题的文献中均利用变分方法获得弱解的存在性,而除文献[2-3]中给出一些表达式外,文献[2]的引用文献及文献[4-12]中均没有给出表达式。受文献[2-4]启发,本文考虑时问题(1)古典解的存在性,类似可以证明u=u时本文的结论同样成立。a、b、λ的符号在问题(1)中相对具有对称性, 从而在研究中当a0时总假设a>0,其他情形相应按符号对称便已经包含其中。本文主要结论包括定理1~3。 定理1如果a>0,则结论①~③是古典解。 定义1设Ω⊆RN,f:Ω→R,xf(x),任给x0∈Ω,>0,若存在δ>0,使得|x-x0|<δ时总有|f(x)-f(x0)|<ε,则称f是Ω到R的连续函数。Ω到R的连续函数全体,记为C(Ω,R)。 定义2设Ω⊆RN,f:Ω→R,xf(x),若则称f∈Li(Ω)(i是正实数)。 当然,如果一个函数存在连续导数,根据Green公式可以证明它也是弱导数。 (2) 则称u为问题(1)的一个弱解。 (3) 根据定义4、5立即可知,如果u为问题(1)的一个古典解,则u也是问题(1)的一个弱解,因为弱解的2阶偏导数不一定连续存在,所以弱解不一定是古典解。下面只证的情形。 (4) 设i>1,考虑关于t的方程 (5) 当b≠0时,方程(5)总有实值或复值的形式解 (6) (7) 1)如果a>0且b=0,则问题(1)退化为: 2)如果a>0,b>0,则对任给的λ∈R,如果λ>0,必存在k∈N*,k≥1,使得λ 综上不仅证得定理1古典解的存在性,还给出一类解的抽象形式,具体表达式的例子见第3章。 定理2的证明这部分的证明依赖于定理1证明的一些结果。如果a=0,则对i>1的特征值μi及其对应的特征函数φi,方程(5)变成 若再有bλ<0,则方程(5)变换得到的关于t的方程总有实数解 问题(1)有无穷多古典解,可以表示为 如果a=0时u是问题(1)的解,则 特别地,取v=u便可以得出a=0且bλ≥0时只有平凡解。 定理3的证明根据定义1,问题(1)的每一个古典解un必然都满足 再根据定义2可得 都是问题(1)的古典解,并且 (8) 至此,定理3的证明已经完成。但是,作为扩展,考虑退化的Kirchhoff型问题,即 (9) 式中Ω⊂RN(N≥1)是光滑有界域,λ为任意正数,u=u或是∂Ω上的单位外法向量(注意N=1时Ω表示连续区间,的边界值为u′(x)在端点处的单向导数值),那么定理4成立。 定理4对任意λ>0(可以是常数也可以是参数),问题(9)有无穷多古典解。 其表明问题(9)与同边值条件的问题-Δu=λu特征值有关,注意方程(9)不是线性的,可以发现un是解时后者I(tun)≡0,而前者I(tun)≢0,并且t≠1时不是实值解。 (10) (11) 根据式(10)和(11),对任意实数λ和μ,有 当b≠0时考虑关于μ的方程 (12) 通过式(12)可得 (13) (14) 对所有n>N而言都是问题(1)的古典解, 因此问题(1)有无穷多古典解。 而在a>0,b<0的前提下只有u≡0满足。所以a>0,b<0且λ≤λ1时问题(1)只有零解。 (15) 也即特征值问题: 具有无穷多古典解可以表示为式(15),而a=0且bλ≥0时类似于例6可得出问题(1)只有零解。 作为补充,对于Kirchhoff型问题来说,含有正模量时文献[15]考虑了带有线性项的一种广义形式并利用本文的方法获得无穷多古典解,文献[16]考虑了带有临界指数时的一种广义形式并利用达到函数获得古典解,这些问题都可以推广到负模量的情形;而含有负模量情形的研究渊源在文献[2]中有具体叙述,在随后的研究情况参见文献[17-20]及其引用文献中的叙述。最新的结果中,文献[17]在无界域上考虑了带有除了-1指数外的所有指数情形并构造出无穷多古典解,同时给出有界域上无边界限制时的古典解(见文献[18]),文献[19]推广到了变指数情形并利用变分方法获得弱解的存在性,文献[20]利用达到函数获得临界指数情形的无穷多解。注意到在无穷多解的文献中,不难发现,文献[17-18]在RN的子集中构造出无穷多解的解析式,文献[19]的结论是存在无穷多弱解,除文献[15]外,本文中无论是方法、研究范围还是所得到的结果,均体现出明显的差异。而对于这一类问题,它们也属于微分方程边值问题的一种,也可以利用文献[21-22]等所采用的不动点理论来研究多重解的存在性,当然也可以利用Ljusternik-Schnirelman极小极大原理获得无穷多解,建议使用更多方法研究这类问题,得到更多结果。
1 问题及主要结果
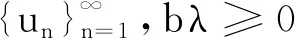
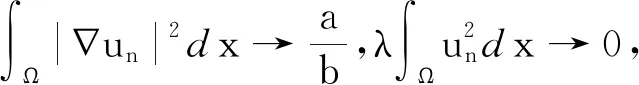
2 主要结果的证明
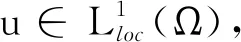
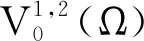
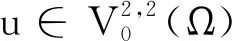
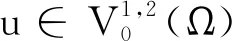
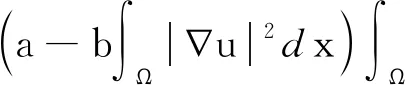
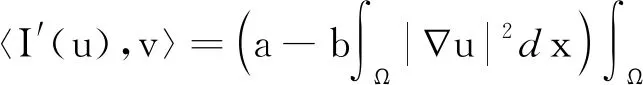
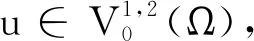
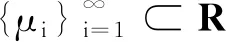
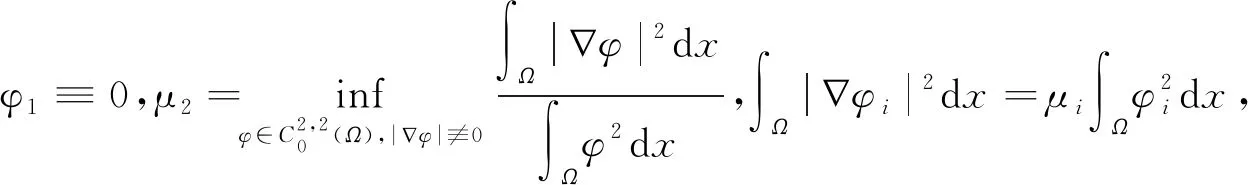
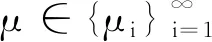
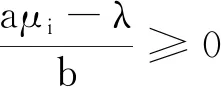
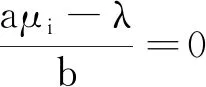
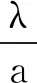
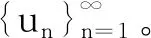
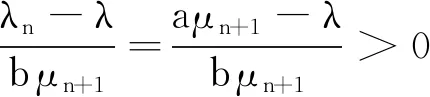
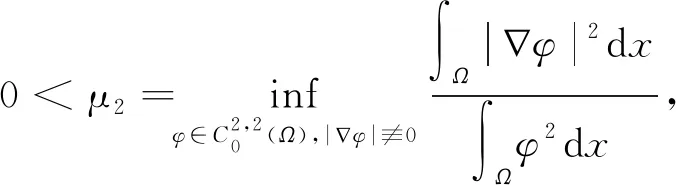
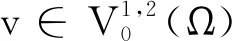
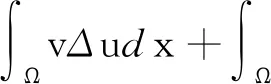
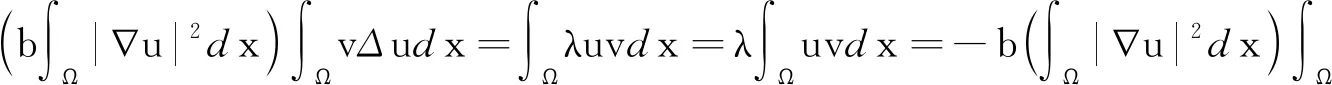
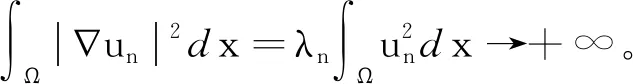
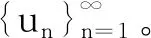

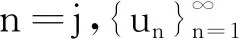
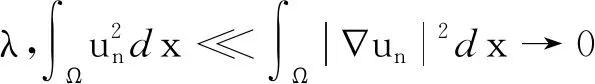
3 定理1和定理2的结论举例
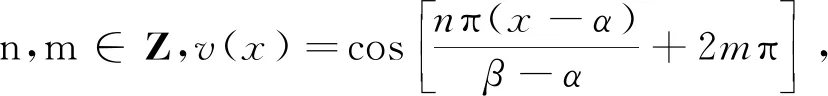
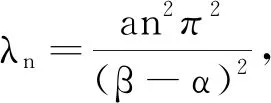
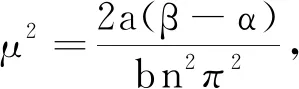
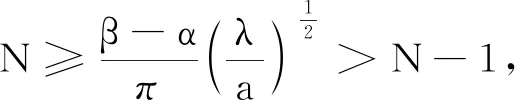
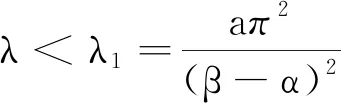
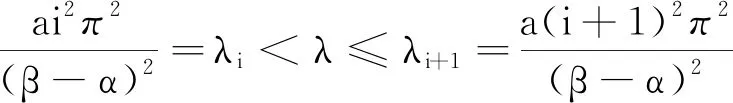
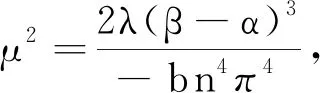
4 总结与展望


