含等级治疗率与不完全康复率的SIRS模型的分岔分析

黄春贤，周效良

(1. 闽南师范大学 数学与统计学院，福建 漳州 363000; 2. 岭南师范学院 数学与统计学院，广东 湛江 524048)

传染病严重威胁人类的生存和发展。14世纪中叶，黑死病经过几次爆发，由亚洲传到欧洲，三分之一的欧洲人因此而死亡。1720年至1722年间爆发在法国的腹股沟腺炎瘟疫令马赛失去了一半的人口[1]。在现代，人们卫生意识和社会医疗水平已今非昔比，但过度药物治疗使病毒产生抗药性等问题，往往导致新型病毒的产生，这使得对传染病的防治仍需严阵以待。因此，传染疾病的控制仍然是现代社会亟待解决的问题[2-3]。

研究传染病模型能为传染疾病的控制提供有效的措施[4]。Kermack等[5]于1927年应用动力系统原理在假设人口不同类成员之间的流率相对简单的基础上建立经典的SIR传染病模型；随后一些学者在此基础上考虑了SIS模型[6-8]。SIR模型和SIS模型均是在极端情况下建立的，SIR模型仅考虑患病个体经过治疗必定康复成为具有免疫能力的个体[9]；SIS模型只考虑患病个体完全没有获取免疫能力。Gomes等[3]就该问题建立了一类非理想免疫的传染病模型，通过分析平衡点的性质，给出一些降低传染病流行的疫苗接种措施；Gomes等[10]又考虑一类具有非理想免疫和非线性发生率的传染病模型，得到该模型参数穿越对应临界值时会有后向分岔、振动和Bogdanov-Takens分岔。为了更好地描述传染病的传播，马知恩等[11]建立了一类SIRS模型，该模型考虑患者经过治疗，可能获取完全的免疫能力或者没有获得免疫能力而再次成为易感者。在某些情况下，传染病的发生率并不是双线性的，因此，Lu等[12]考虑了一类具有广义非单调和饱和发生率的SIRS模型，得到了该模型随着参数的变化会发生鞍结分岔、Bogdanov-Takens分岔、Hopf分岔等。

White等[13]建立了一类海洛因毒品传播模型，并给出该模型无海洛因吸食患者平衡点的局部稳定性分析以及有吸食患者平衡点的存在性；Mulone等[14]通过应用特征方程和庞加莱-本迪克松定理对文献[13]的模型的全局稳定性进行了分析；海洛因吸食个体通过治疗成为康复个体需要一定的时间周期，因此Liu等[15]以及Huang等[16]都考虑了分布式的时滞项，前者得到了无海洛因吸食患者平衡点的全局稳定和有吸食患者平衡点的局部稳定条件，后者得到有吸食患者平衡点的全局稳定性的条件。Muroya等[17]对轻度海洛因传播的情况提出如下带有等级治疗率以及不完全康复率SIRS模型

(1)

得到模型(1)的基本再生数为

(2)

并给出了无海洛因吸食患者平衡点的全局稳定和有吸食患者平衡点的全局稳定条件分别为R0<1和R0>1，式中：S、I、R分别是总人群中易感个体的比例、患病个体的比例和康复个体的比例；d是新出生的人口比例，假定出生人口比例等于死亡人口的比例；β是易感个体与患病个体接触成为新的患病个体的概率；ε是等级治疗率；δ表示康复个体因为没有获得抗体而转化成易感个体的比率；γ是患病个体的成为康复个体的比率；σ代表康复个体因为不完全治疗而再次成为患病个体的比率。该系统所有参数均是非负常数。

2016年，史学伟等[18]在模型(1)基础上加入信息变量，得到了系统存在Hopf分岔；2017年，Ma等[19]在模型(1)的基础上，进一步考虑非线性发生率以及海洛因吸食者不能通过自身意志克服毒瘾再次成为易感者，对一类具有非线性发生率的海洛因模型进行了分岔分析，得到系统存在Bogdanov-Takens分岔。

本文研究模型(1)的分岔性质。在系统(1)的极限集S+I+R=1上考虑系统(1)，可以得到系统(1)的约化系统[20-21]如下：

(3)

约化系统(3)的稳定性与原系统(1)的稳定性等价。为方便表示，令θ1=d+ε+γ，θ2=d+δ+σ。

1 平衡点分析

本章研究系统(3)平衡点的类型。系统(3)仅存在2个平衡点E0(0, 0)和E1(I*,R*)，其中：

(4)

(5)

定理1系统(3)的无病平衡点E0(0, 0)只为下面3种情况之一：

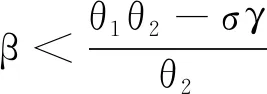
证明系统(3)在平衡点E0(0, 0)处的Jacobi矩阵为

(6)

特征方程为

λ2+a11λ+a12=0，

(7)

式中a11=θ1+θ2-β，a12=-βθ2+θ1θ2-σγ。易知

(θ1+θ2)2-2β(θ1+θ2)+β2+4βθ2-4θ1θ2+4σγ=

β2-2β(θ1-θ2)+(θ1-θ2)2+4σγ=

[β-(θ1-θ2)]2+4σγ>0。

因此，特征方程(7)存在2个不同的实特征根。根据韦达定理得：

定理2系统(3)的地方病平衡点E1(I*,R*)只为下面3种情况之一：

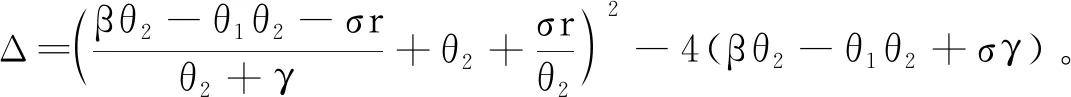
证明系统(3)在平衡点E1(I*，R*)处的Jacobi矩阵为

(8)

特征方程为

λ2+a21λ+a22=0。

(9)

把式(4)和式(5)代入得：

2 分岔分析

本章主要研究系统(3)的分岔性质。定义系统(3)的无病平衡点与地方病平衡点的距离为

d=‖E1-E0‖2，

(10)

(11)

引理1[22]考虑带参数φ的常微分方程组

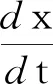
(12)

假定0是系统的平衡点，即对任意φ满足：f(0,φ)≡0。

②对应于零特征值，A有一个非负的右特征向量ω和一个左特征向量υ，记

(13)

(14)

则当a<0，b>0时，该系统发生前向分岔。该分岔的分岔图如图1所示。

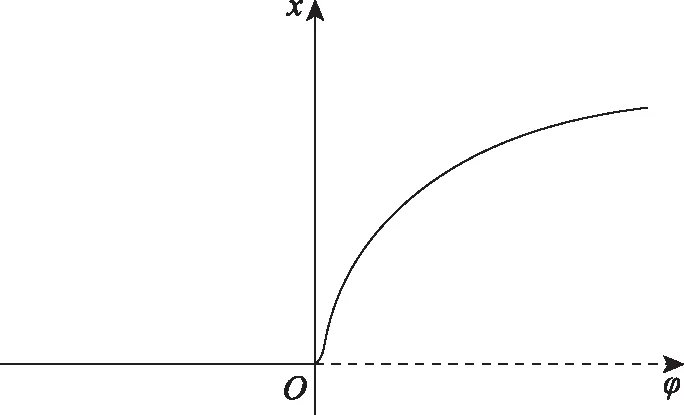
图1 a<0,b>0时系统的前向分岔Fig. 1 Bifurcation diagram of forward bifurcation for a<0, b>0

(15)

可解得特征值为

(16)

因此，Jacobi矩阵J(E0,β*)有一个零特征值，且其他特征值均为负实部的。

设W=(w1,w2)T是Jacobi矩阵J(E0,β*)的右特征向量，满足J(E0,β*)W=0，即

(17)

解得

W=(θ2,γ)T。

(18)

设V=(v1,v2)T是Jacobi矩阵J(E0,β*)的左特征向量，满足VJ(E0,β*)T=0，解得

V=(θ2,σ)Τ。

(19)

由系统(3)得到：

(20)

计算该系统在无病平衡点E0的二次偏导数：

易知：

(21)

(22)

由引理1，定理3得证。证毕。

3 数值模拟

本章根据以上理论分析，通过数值模拟，给出系统(1)的相图和状态变量随时间变化的曲线图，系统的参数选为下面2种情形：

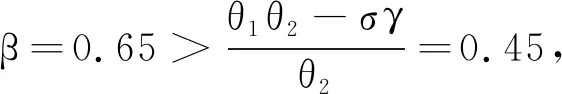
图2 β<β*时系统(1)的相图Fig. 2 Phase diagram of system (1) for β<β*

图3 系统(1)初始值为(0.45, 0.28)的曲线Fig. 3 Curves of system for initial condition (0.45, 0.28)

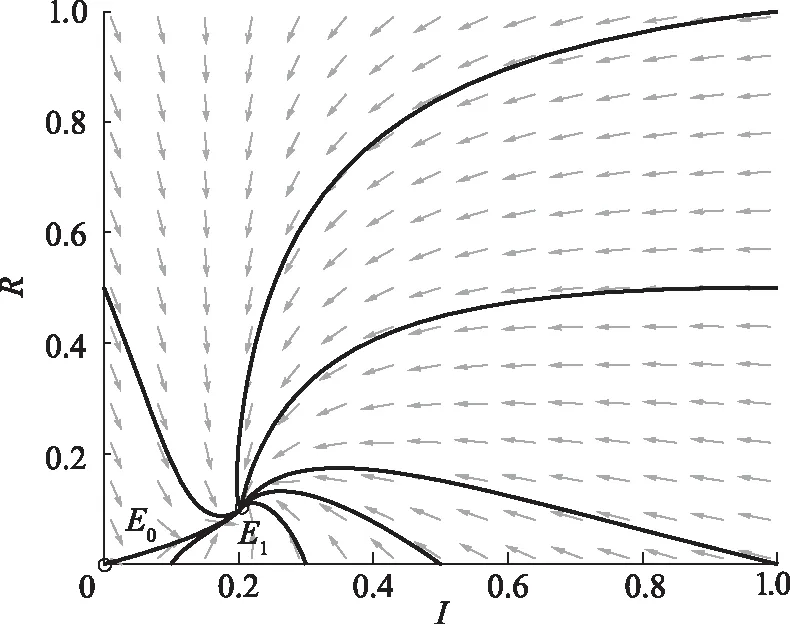
图4 β>β*时系统(1)的相图Fig. 4 Phase diagram of system (1) for β>β*

图5 系统(1)初始值为(0.004 5, 0.002 8)的曲线Fig. 5 Curves of system for initial condition (0.004 5, 0.002 8)

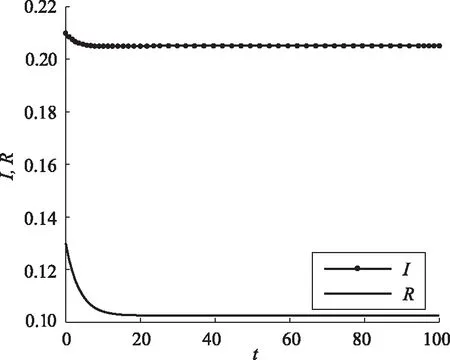
图6 系统(1)初始值为(0.21, 0.13)的曲线Fig. 6 Curves of system for initial condition (0.21, 0.13)

4 结语

本文通过对一类具有等级治疗率及不完全康复率的SIRS模型的平衡点类型进行分析，得到β<β*时，系统仅存在一个稳定的结点E0(0, 0)；当β>β*时，系统仅存在一个不稳定的鞍点E0(0, 0)和稳定的平衡点E1(I*,R*)，发现该系统存在前向分岔，并对其进行严格证明；最后数值模拟验证系统参数β越过临界参数值β*时系统相图的拓扑结构发生改变。