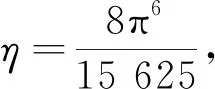一类分数阶微分方程的反周期边值问题
左佳斌,贠永震
(1. 河海大学 理学院,江苏 南京 210098; 2. 吉林工程技术师范学院 应用理学院,吉林 长春 130052)
在近十几年里,分数阶微分方程在多孔介质、流体力学、自动控制和电动力学等科学领域得到广泛应用,分数阶微分方程理论得到快速发展[1-19]。在对分数阶微分方程理论研究的过程中,其边值问题作为重要的研究方向,很多学者对此作了研究,得到大量的研究结果[12-19]。 反周期是物理学中一种重要的现象,对于一个变化的物理过程,可以转化为一个反周期的数学模型。对于分数阶微分方程反周期边值问题,现在已经有学者作了研究,得到了一些研究结果[12-14,20-21]。文献[12]研究了下面一类分数阶微分方程反周期边值问题解的存在性
(1)
式中CDq为q阶Caputo分数阶微分,f为给定的连续函数。文献[12]利用一些不动点定理得到该边值问题(1)解的存在性结论。
在血液流动、流变学和材料科学等许多科学领域,出现了带有p-Laplace算子的分数阶微分方程的数学模型,因此,对于带有p-Laplace算子的分数阶微分方程边值问题解的存在性,很多学者进行了研究并取得大量研究结果[13-14,17-18]。文献[17]研究了下面一类带有p-Laplace算子的分数阶微分方程边值问题解的存在性
(2)
式中:ai≠1,i=1, 2, 3;f∈C([0,T]×R,R);x(t)∈C2([0, 1],R)。利用Banach压缩映像原理,文献[17]得到该边值问题(2)在一定条件下解的存在性结论;在文献[12]中,作者研究了不具有p-Laplace算子的分数阶微分方程反周期边值问题解的存在性。需要说明的是文献[17]中的边值条件不是反周期形式。目前对具有p-Laplace算子的分数阶微分方程反周期边值问题解的存在性的研究不多[13-14,20-21]。受上述文献启发,本文考虑下面一类带有p-Laplace算子的非线性分数阶微分方程反周期边值问题解的存在性
(3)

1 相关定义及引理
第1章给出一些定义及相关引理,见文献[1,17,19]。
定义1[1]令α>0,函数u:(0, +∞)→R的Riemann-Liouville分数阶积分定义为
定义2[1]令α>0,函数u:(0, +∞)→R的Caputo分数阶微分定义为
式中n-1≤α u(t)=c0+c1t+c2t2+…+cn-1tn-1, 式中ci∈R,i=1, 2, …,n-1,n=[α]+1。 引理2[1]令α>0,则 式中ci∈R,i=1, 2, …,n-1,n=[α]+1。 引理3[17]如果p>2且|x|、 |y|≤M,则对于p-Laplace算子φp,下面不等式成立 |φp(x)-φp(y)|≤ (p-1)Mp-2|x-y|。 引理4[19](Krasnosel’skiis不动点定理) 设Ω为Banach空间X上的有界闭凸非空子集,算子Φ、Ψ满足:(i)Φu+Ψv∈Ω,其中u、v∈Ω;(ii)算子Φ是紧的且连续;(iii)算子Ψ是压缩映像,则存在z∈Ω,使得z=Φz+Ψz。 第2章给出分数阶微分方程边值问题(3)的Green函数。 引理5若1<α≤2,函数y∈C[0, 1],则分数阶微分方程边值问题 有唯一解 式中 即 因为1<α≤2,利用引理2可知 根据Caputo分数阶微分的性质可得 因此, 第3章利用p-Laplace 算子的性质、Bnanach压缩映像原理和引理4给出分数阶微分方程边值问题(3)解的存在性定理。 定义算子F:X→X为 求边值问题(3)的解的存在性转化为求算子F是否存在不动点。 定理1假设1 (H2) 存在常数L>0,使得当t∈[0,T]时,对任意函数u、v∈X,有|f(t,u(t))-f(t,v(t))|≤L|u-v|成立; 则边值问题(3)存在唯一解。 证明由条件(H1)可得 因此,‖(Fu)(t)‖≤r,即F:Br→Br成立。 又因为对任意u、v∈Br,当t∈[0,T]时有 |(Fu)(t)-(Fv)(t)|≤ 由条件(H3)可知,N<1时 ‖(Fu)(t)-(Fv)(t)‖≤N‖u-v‖。 故算子F在Br内为压缩映射,由Banach压缩映射原理可知,算子F在Br内存在唯一不动点,即边值问题(3)存在唯一解。证毕。 按徐演的说法,这个版本本来要作为“云南民族民间文学丛书之一”出版,但因为这时由宣传部领头的,具体由一群学生组成的调查又已经启动,所以出版暂停。徐嘉瑞甚至“拿出这份由出版社已经打印成校样的整理稿,以完全无私的精神,无条件地全部交给了学生们”。 定理2假设1 则边值问题(3)至少存在一个解。 因为对任意u、v∈Br1,当t∈[0,T]时有: |(Φu)(t)+(Ψv)(t)|≤ 因此,‖Φu+Ψv‖≤r1,即Φu+Ψv∈Br1。对任意u、v∈Br1,当t∈[0,T]时有: |(Ψu)(t)-(Ψv)(t)|≤ ‖(Ψu)(t)-(Ψv)(t)‖≤N1‖u-v‖, 故算子Ψ在Br1内为压缩映射。 根据Φ的定义易知其连续。 因为对任意u∈Br1,有 因此,算子Φ一致有界。 又因为对任意t1、t2∈[0,T],当t1 因此,当t2→t1时,有‖(Φu)(t2)-(Φu)(t1)‖→0,即算子Φ等度连续。由Arzela-Ascoli定理,Φ在Br1内为紧算子,故由引理4可知边值问题(3)存在至少一个解。证毕。 本章给出2个例子验证本文得到的结论。 (4) 又因为 由定理1可知,边值问题(4)存在唯一一个解。证毕。 (5) 由定理2可知,边值问题(5)至少存在一个解。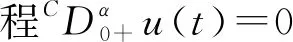

2 Green函数
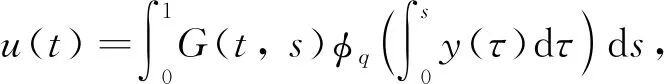
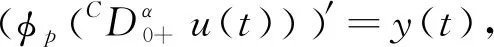
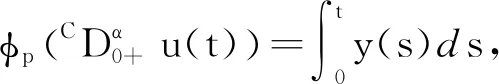

3 解的存在性

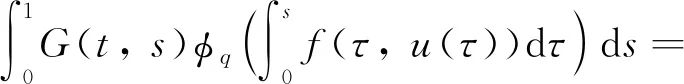

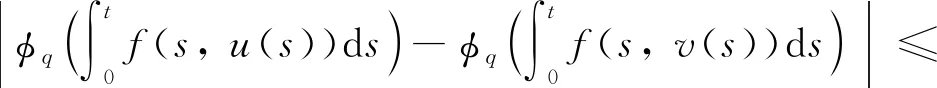
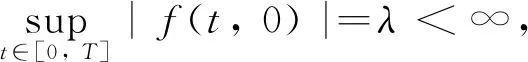
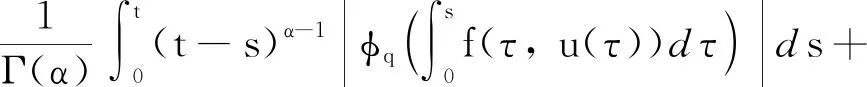





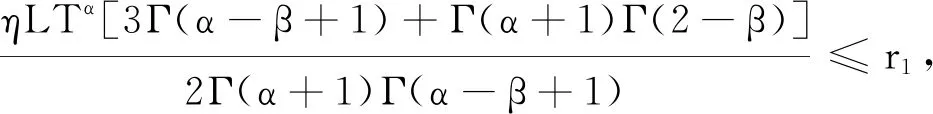


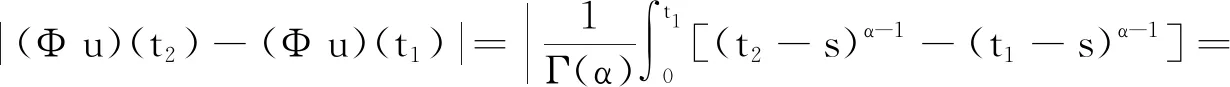
4 例子
例1 证明下面一类分数阶微分方程反周期边值问题解的存在性
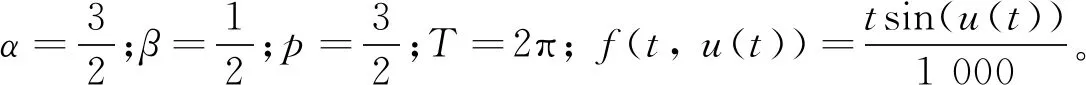
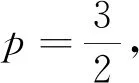

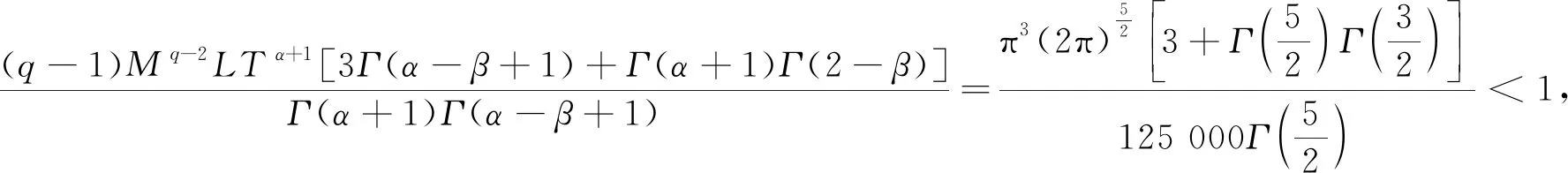
例2 证明下面一类分数阶微分方程反周期边值问题解的存在性