基于自适应局部特征的蛋白质三维结构分类

张汝昌，邱 杰，王明堂，陈庆锋*

(1. 广西大学 计算机与电子信息学院，广西 南宁 530004； 2. 玉林师范学院 计算机科学与工程学院，广西 玉林 537000)

蛋白质是由氨基酸以“脱水缩合”的方式组成的多肽链经过盘曲折叠形成的具有一定空间结构的物质。人类的许多疾病都与某些蛋白质功能有关。对蛋白质结构和功能的深入研究，能够为治疗人类疑难病症提供更好的助力[1]。蛋白质的结构与其功能密切相关，结构决定功能已经成为生物学家的共识。假设结构和功能在进化上是连续的，由蛋白质结构之间的相似关系，可以让科学家推断或预测新发现的与已知蛋白质结构相似的蛋白质的功能[2]。结构相似的蛋白质其生物功能也往往相似，最终决定蛋白质功能的是蛋白质的空间自然折叠的三维形状[3]。蛋白质的三维结构目前主要的测定方法有：X射线晶体衍射、电子晶体学电镜三维重构以及核磁共振[4]等。定量地比较2个蛋白质三维结构来评估它们的相似性是生物信息学里一个重大的挑战，成功的比较可以为结构生物学、细胞生物学和生物化学中的一些重要问题提供答案[5-6]。随着PDB(protein data bank)中蛋白质结构的数量逐年增大，蛋白质之间的网络关系变得越来越复杂[7-8]，如何有效利用现在已知的数据去预测未知蛋白质的功能及对其进行分类已经成为一个新的难题。

利用计算机科学分析该问题已是当前的一个热点。基于数字化技术计算分类蛋白质结构的方法主要有：SCOP[9](structural classification of proteins)、CATH[10](class, architecture, topology and homologous superfamily)、TM-score[11-12]、FSSP[13](families of structurally similar proteins)、DALILITE[14]等。当前，通过这些方法已经获得了一些蛋白质结构分类的数据库。除了上述方法，还有通过结构对齐算法分类蛋白质结构的方法，如CE[15]、VAST[16]、SSAP[17]、FAST[18]等，最早提出并被广泛应用的是RMSD方法[19]。大部分对齐算法时间复杂度较高，在大规模数据集上难以应用。当前，对预测未知蛋白质功能和分类的主流评价指标是模板建模评分(template modeling score, TM-score)，它是衡量2个具有不同三级结构的蛋白质且与蛋白质的大小无关的全局折叠相似性度量。TM-score是一个标准化的度量，其值在[0, 1]内，其值大于0.5时说明在SCOP/CATH中有相似折叠性，等于1时，这2个蛋白质是一致的[20]。为了减少计算复杂度，一些不依赖结构对比的方法被提出，如基于图理论的方法[21-22]、基于Cα距离矩阵的方法[23]。为了简化对三维骨架进行空间配准操作的复杂问题，Taylor等[24]将蛋白质的空间坐标转化为距离矩阵的量化表示。在此基础上，Choi等[25]提出了一种基于局部特征频率的计算蛋白质相似性的方法，该方法把蛋白质结构的Cα距离矩阵划分出许多具有重叠元素的子矩阵，每一个子矩阵都代表蛋白质三维结构在空间中的局部特征，比如α螺旋结构、β折叠结构。从这些大量子矩阵所代表的蛋白质局部特征中做聚类分析，划分成k类局部特征的子矩阵集合，由此将每个蛋白质结构抽象成k维欧氏空间的特征点，求出发生k类局部特征的频率(LFF)，每个蛋白质的距离矩阵在做相似性比较之前可以先转成LFF，通过计算LFF之间的距离间接得到蛋白质的相似性，这样计算得出的结果和SCOP的蛋白质结构分类具有很好的一致性。但是这种方法主要是靠人工枚举选择蛋白质局部特征的大小和聚类中心点的数量，计算量大的同时也未必得到最好的局部特征。

本文对LFF做改进，提出自适应数据集的局部频率向量ALFF。首先，为了选择更好的蛋白质结构局部特征来计算蛋白质结构相似性，引进了OTSU算法[26]，该算法能确保选出来的子矩阵在不同蛋白质之间有更大的区分性，提高计算的相似度结果；同时还使用MeanShift[27]代替k-medoids做聚类分析，其可以根据数据集的特点，自动计算出簇的数量，而不需要人工参与。其次，在数据预处理中，将冗余的子矩阵去除，减少了接近一半的计算量。最后，本文随机选择多组SCOP的蛋白质结构数据进行相似性比较，实验结果显示：在蛋白质结构class、fold、superfamily以及family分类层面上，ALFF比LFF有更好的一致性；和TM-score评分比较，ALFF在蛋白质结构相似性上有更好的结果，其准确性有明显提升。

1 材料和方法

1.1 局部特征频率向量(LFF)

Choi等[25]在3 792个非冗余折叠结构中随机选出100个蛋白质，首先，对每个蛋白质p计算其中任意2个Cα原子之间的距离，得到一个对称的距离矩阵Dp={dp(i,j):i,j=1,2,…,sp}，式中dp(i,j)表示该蛋白质的第i和第j个Cα原子之间的欧氏距离，sp表示Cα原子个数。这个矩阵用二维信息表示三维的折叠结构，也和蛋白质的骨架一一对应，在一定程度上可以代表这个蛋白质的整体结构。接着，使用滑动窗口(窗口大小为m的矩阵)的方式，在距离矩阵上划分出子矩阵集合

(1)

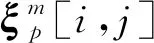
(2)

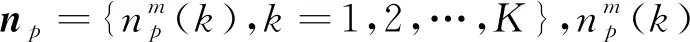
1.2 自适应的局部特征频率向量(ALFF)

Choi等[25]通过重叠子矩阵的聚类分析，发现蛋白质三维结构可以使用k(k=100)种m×m(m=10)的特征子矩阵的发生频率来表示，这种方法计算出来的结果与SCOP数据库对蛋白质结构的分类具有很好的一致性。然而，这个方法也有一些缺陷，比如参数m和k的选择，m的大小和所选蛋白质的局部特征密切相关，而k也会根据数据集的不同有不一样的结果。Choi等[25]从SCOP数据库的3 792个非冗余折叠结构中随机选择了100个，利用有限枚举法(m=8，10，12，16；k=50，100，150，200，250，300)得到实验最优取值m=10，k=100。这样选择参数有以下不足之处：1)100个非冗余结构不能完整表征已经解析的所有结构和特点，如果实验中换了一组数据，那么由于蛋白质的结构不同，LFF根据这些参数(m=10，k=100)得到的局部特征很有可能不适合表示新的数据，所以从中提取的特征子矩阵更适用于描述与此100种结构类似的结构，而不适用于这100种结构以外的结构；2)有限枚举法在取值的优化上具有明显的局限性，因为计算复杂度较大，还需要人工画图观察参数变化以选出最优；3)由于距离矩阵是对称的，所选出来的子矩阵在结构上存在冗余，实验忽略了子矩阵沿着对角线对称等效分布的情况，可能将等效的子矩阵归属到不同的特征子矩阵。基于这3点不足，本文在Choi等[25]的LFF方法上做了一些改进，提出可以自动适应数据集的LFF算法，即ALFF。ALFF能够根据所选择的数据集选出最好的m和k这2个参数，而不需要花大量时间通过枚举来手工选择参数。ALFF算法先采用OTSU算法得到较优的子矩阵，其大小为m，再使用MeanShift聚类算法得到局部特征的数量k，最后在做相似性比较前对数据进行预处理并去除对称矩阵等效的子矩阵。

1.2.1 最大类间方差法(OTSU)

OTSU是日本学者大津于1979年提出的一种自适应的阈值确定方法[26]。在计算机视觉和图像处理中，OTSU算法被用来对基于聚类的图像进行二值化。该算法按图像的灰度特性，将图像分成背景和目标2部分。背景和目标之间的类间方差越大，说明构成图像的2部分的差别越大，当部分目标错分为背景或部分背景错分为目标时都会导致2部分差别变小。因此，使类间方差最大的分割意味着错分概率最小[28]。由此，本文将OTSU算法拓展到ALFF算法参数m的优化上，对于所选择的蛋白质数据集，划分出来的子矩阵是否能够很好地表示蛋白质的局部特征，关键在于子矩阵大小m的确定。假定所选择出来的所有局部特征能使这些蛋白质区分度达到最大，使得蛋白质结构的类间方差最大，则对应的局部特征是最合适代表蛋白质的局部结构。在对蛋白质数据划分子矩阵的时候，m的取值范围是[2,L]，其中L是所有蛋白质的距离矩阵中最小的维度。记ni表示子矩阵维度为i的数量，N=n2+n3+…+nL，则子矩阵维度服从概率分布

(3)

现在根据假定的阈值t，把子矩阵分为2类：X1记为子矩阵维度在[2,…,t]，X2记为子矩阵维度在[t+1,t+2,…,L]，然后在以上子矩阵的概率分布下，有：

(4)

(5)

背景和目标的灰度值分别是：

(6)

(7)

2～L的累计值为

ρ=λ1×ρ1+λ2×ρ2。

(8)

根据以上关系，类间方差有

σ=λ1×(ρ1-ρ)2+λ2×(ρ2-ρ)2。

(9)

当类间方差σ取得最大时，对应的t即为最优，所以

(10)

本文后面会用多组实验验证OTSU算法选择参数m的有效性。

1.2.2 MeanShift

在LFF方法中，聚类的簇的数量k，即局部特征数量，同样是一个比较重要的参数。LFF使用有限枚举法遍历一定数量的k值，然后人工选择认为比较好的参数k，如果要枚举的m、k的个数分别为nm、nk，那就一共需要做nm×nk次聚类实验，这是一个很耗费时间的过程。本文方法是在蛋白质结构中划分了大量有重叠结构的子矩阵，如何选择k才能使得最后得到的频率向量能准确地反映蛋白质的结构是一个核心问题，当k的数量未知时，枚举法也很难选出好的结果。因此本文目标是能找到一种能够自动发现聚类中心点的算法，不需要人为干预蛋白质局部特征的数量k，而MeanShift方法就是能满足上述需求的一个算法。MeanShift主要思想是将数据特征空间视为先验概率密度函数，对于输入的数据被认为是一组满足某种概率分布的样本点，所以特征空间中数据最密集的地方对应概率密度最大的地方，概率密度的质心就可以被视为概率密度函数的局部最优值，即所求的聚类中心点。

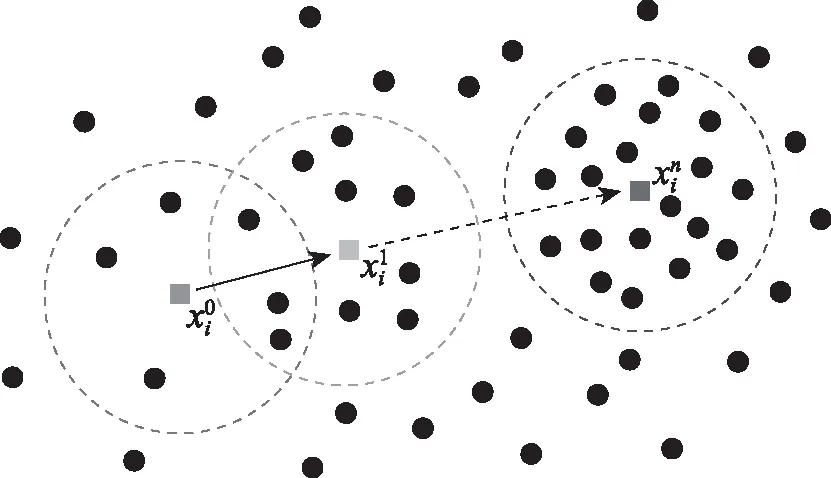
图1 MeanShift收敛过程Fig. 1 Convergence process of MeanShift

对于每一个样本点，以它为中心的某个范围所有样本的均值作为每次迭代新的中心，窗口的重心都向数据更密集的地方移动[29]。图1直观地描述了MeanShift一次移动过程，图中的大圆圈代表当前的限制条件，箭头是本次迭代所取得的平均偏移向量。可以看出，每次的中心点都会向数据密集的地方移动，直到算法收敛。对于给定d维空间Rd中的中心点oi，第l次迭代的坐标更新由式(11)给出

(11)

给定N(oi)为中心点oi在距离h内所有的近邻点，Mh(x)为每个质心x计算的平均移位向量，其指向点密度最大增加的区域，有效地将质心更新为其邻域内样本的平均值，MeanShift向量的基本形式为

(12)

式中K为核函数。在MeanShift算法中引入核函数的目的是使得随着样本与被偏移点的距离不同，其偏移量对均值偏移向量的贡献也不同。核函数常被用在机器学习中，可以减少计算量。ALFF使用的是高斯核，定义为

(13)

最终，所有类的数量就是需要找的k值。使用MeanShift算法主要有2个优势：1)对任意形状的数据都可以较好地聚类；2)根据数据的分布特点自动找到比较合适的聚类数量。

1.2.3 ALFF算法步骤

基于自适应的局部特征频率向量计算蛋白质三维结构的相似性算法步骤如算法1中伪代码所示。算法的输入有：1)所有蛋白质的Cα距离矩阵Dmats；2)MeanShift中近邻范围参数h；3)MeanShift收敛阈值ε。算法输出是一个蛋白质相似性矩阵S。算法首先初始化参数，使用变量m遍历[2,L]区间，L是长度最小的蛋白质的Cα数量；然后根据m从距离矩阵划分出所有子矩阵，计算对应的类间方差并选出方差最大的对应的子矩阵大小m*；最后通过MeanShift对所有的m*×m*的子矩阵聚成k类，并统计每个蛋白质的子矩阵在k个中心点发生的频率得到ALFF，通过ALFF使用余弦相似性计算蛋白质相似度。

算法1ALFF计算蛋白质相似性。

输入：蛋白质的Cα距离矩阵Dmats；近邻范围h；MeanShift收敛阈值ε。

输出：蛋白质相似性矩阵S。

1. 初始化：L=min_dimensional(Dmats)； // 获取距离矩阵的最小维度作为上限

2.m*=0 // 最优的子矩阵维度

3. sub_mats={} // 子矩阵集合

4. max_σ=-∞ // 当前最大方法

5. form=2→Ldo

6. sub_mats=get_submats(Dmats,m) // 根据子矩阵的大小m划分子矩阵

7.σ=get_variance (sub_mats) // 计算子矩阵为m的类间方差

8. ifσ>max_σthen

9. max_σ=σ

10.m*=m

11. end

12. end

13.Xnew=X=get_submats(Dmats,m*) // 使用m*划分子矩阵

14. repeat

15.C=0 // 每次迭代的cost为0

16. fori=0→n-1 do // 遍历每个样本点

17.x=Xnew[i]

18.N(x)=get_ neighbors(x,h) // 对子矩阵x求最近邻

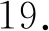
20.C=C+x-Mx// 更新cost

21.Xnew[i]=Mx

22. end

23. untilC<ε

24. ALFF=get_frequency(Xnew,X) //用聚类结果Xnew和原始样本点X求ALFF

25.S=cos_sim(ALFF) // 计算余弦相似性。

2 实验结果及讨论

2.1 局部特征大小分析

本文通过随机选取蛋白质数据做实验，分析OTSU算法的计算结果。SCOP (https://scop.berkeley.edu)是一个根据大多数结构已知的蛋白质的结构和进化关系对其结构域进行分级的数据库，在最新的发行版2.07中，从所有的折叠结构中抽取了14 401个具有代表性结构的蛋白质作为测试数据。在测试数据中随机抽取3组蛋白质，对比可以发现，尽管每组数据的最优m的大小有一定差异，但是通过图2可以看到蛋白质类间方差都是先递增后递减的。图2有3组蛋白质数据，每一组都是100个蛋白质，横坐标是划分子矩阵的大小m，纵坐标是利用OTSU算法通过m得到的类间方差σ，当使用不同维度的滑动窗口划分出子矩阵时，类间方差达到最大时对应的维度就是最优的m，即m*。图2中3组数据g1、g2、g3的m*分别是22、18、26。图3中，实验选择了1 000组蛋白质，使用OTSU算法计算m*，画出频率分布直方图，可以发现m*分布是有规律的，这1 000组蛋白质的m*大多数分布在[8, 30]，其中[14, 26]数量最多，所以理论上任意数据集都可以用OTSU算法计算m*。

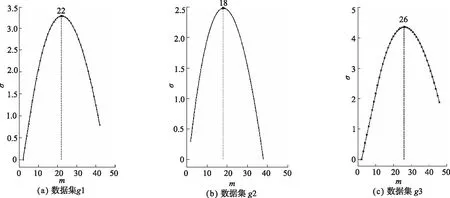
图2 m*和类间方差的关系Fig. 2 Relationship between m* and the variance between classes

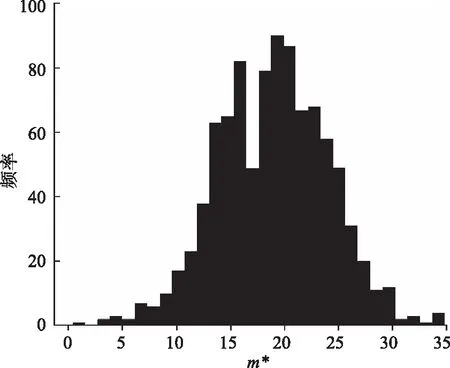
图3 最优m*值的分布情况Fig. 3 Distribution of optimal m*

2.2 算法对比

为了验证OTSU和MeanShift算法计算参数最优值的有效性，本文随机选择5组实验数据，并与LFF、ALFF_OTSU方法做对比实验，其中：ALFF_OTSU方法只使用OTSU优化LFF的参数m，聚类方法和LFF一致，使用k-medoids聚类，k=100；LFF使用参数m=10，k=100；ALFF方法的参数m和k分别使用OTSU和MeanShift算法得出的最优值。实验评估方法为重构距离矩阵和原始距离矩阵的差异对比DME(distance matrix error)[25]。重构距离矩阵的计算方法为：所有的子矩阵聚类完成后，得到k个中心点。对于每个蛋白质最初的Cα距离矩阵，其每个子矩阵被该子矩阵的最近邻(所在簇的中心点)代替，如果替换过程中有重叠的地方，那么每次重叠的位置取两者的平均数代替。

(14)

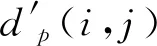
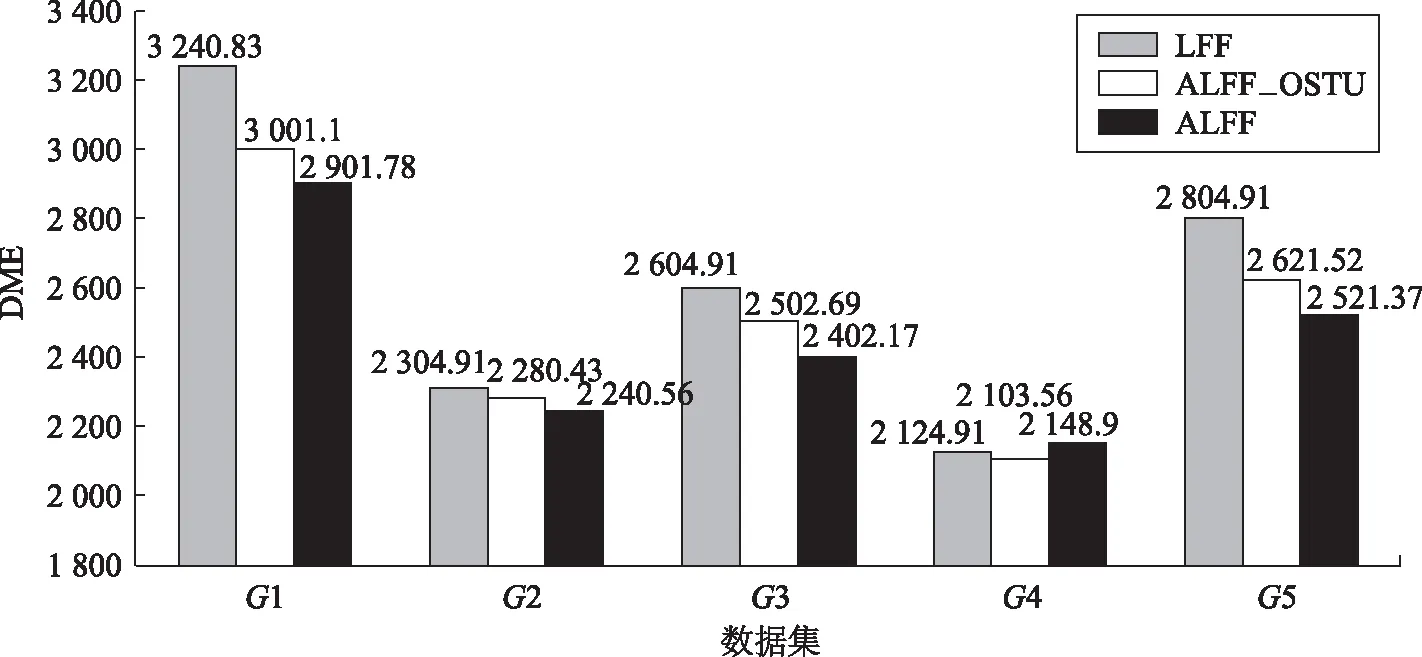
图4 LFF、ALFF_OTSU和ALFF的DME比较Fig. 4 Comparison of DME of LFF, ALFF_OTSU and ALFF

经过以上步骤，每个蛋白质的三维结构都会被表示成一个代表局部特征频率的k维向量，通过这个特征频率向量就可以计算蛋白质的相似性，余弦相似度用向量空间中2个向量夹角的余弦值作为衡量2个个体间差异的大小。余弦值越接近1，表明夹角越接近0°。蛋白质p1和p2的局部频率向量分别是Vp1和Vp2，则它们的余弦相似度定义为

(15)

余弦值的范围在0到1之间，值越大说明2个向量越相似。计算出的蛋白质相似性结果可以和SCOP数据库作比较，SCOP数据库是公认的蛋白质结构分类数据库，表1展示了LFF、ALFF_OTSU和ALFF在SCOP的结构分类上保持的一致性。

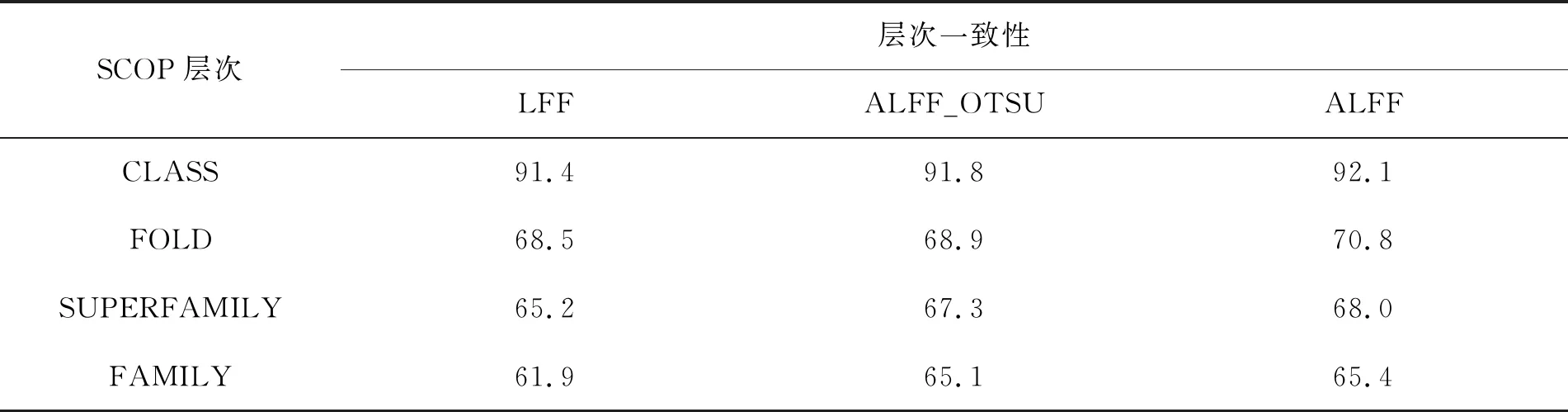
表1 在SCOP中层次分类一致性的比较

在表2中，通过ALFF方法选取了前10组相似度最高的蛋白质对，在SCOP上寻找它们的共同祖先，共同祖先越相近，理论上相似度越高。为验证ALFF的有效性，用ALFF和LFF、TM-score做比较。其中，TM-score方法使用的是在网站https://zhanglab.ccmb.med.umich.edu/TM-score/上的公开服务。蛋白质对的TM-score在[0, 0.17]之间，表示该蛋白质对属于随机结构，在[0.5, 1]之间则表示在相同的折叠下。

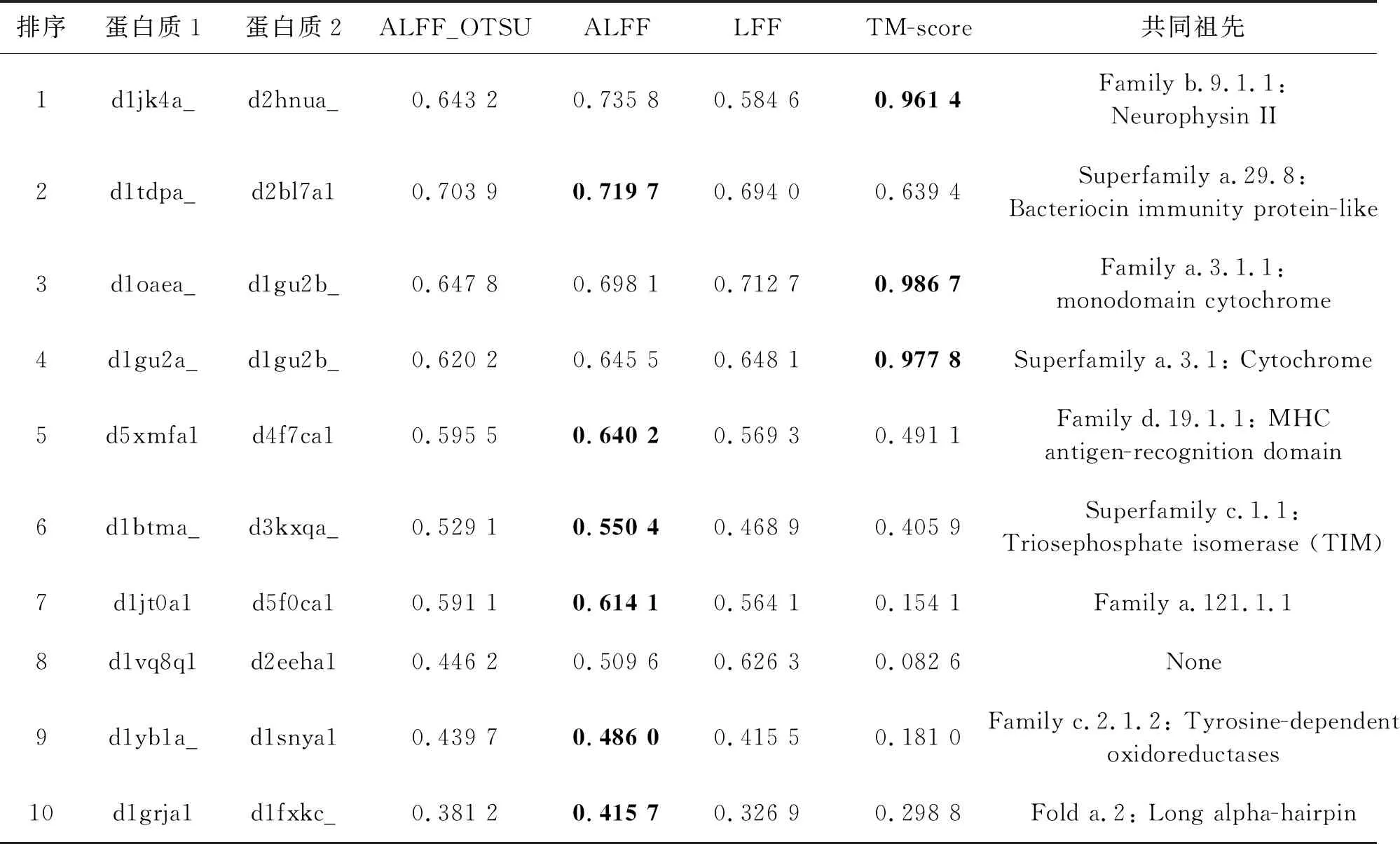
表2 ALFF的TOP10相似性结果和TM-score比较

表2中每组高得分用黑体标注，可以看出，前4组蛋白质在4种方法下都取得比较高的相似性分数，它们的共同祖先是家族或者超家族，而后面除了第8组数据以外，其他组的TM-score都低于0.5，而这些蛋白质都是有共同祖先的，TM-score在该5组数据中不适用。相比之下，ALFF和LFF在后6对蛋白质中仍然有不错的相似性分数，从总体得分上，ALFF略优于LFF。值得注意的是第8组蛋白质没有共同祖先，ALFF和LFF也计算出了比较高的相似性，说明ALFF方法算出这对蛋白质可能有比较多相似的局部特征尽管它们没有共同的祖先。而ALFF_OTSU方法在这10组数据的相似性在ALFF和LFF之间，这证明了OTSU算法在选择蛋白质局部特征大小时的有效性，通过OTSU和MeanShift结合可见，ALFF方法是这几个方法中最优的。

在ALFF方法中，为了避免大量等效的子矩阵对实验结果造成影响，从距离矩阵划分出子矩阵的时候只保留矩阵对角线上方的子矩阵，假设蛋白质数量是N，蛋白质p的距离矩阵维度是np，子矩阵的维度是m，那么N个蛋白质划分得到的子矩阵总数S为

(16)

根据等差数列求和公式，保留下来的子矩阵总数Sstay为

(17)

则总共减少的子矩阵数量为

(18)

从式(18)可以看出，去除的子矩阵接近总数的一半，大大缩小了计算数据量。图5展示了LFF、ALFF和TM-score 3种方法分别计算不同数量蛋白质相似性矩阵的时间开销，横轴表示蛋白质的数量，纵轴表示算法计算相似度矩阵所用的时间，单位为s。观察曲线趋势可以发现，当蛋白质数量比较多的时候，TM-score在计算速度上比较占优势，而LFF和ALFF随着数据量增大，计算的复杂度明显增加，主要原因是这2种方法都基于聚类分析。ALFF经过数据缩减，计算速度明显比LFF提升了许多，计算100个蛋白质的相似性矩阵用时48.13 s，比LFF的79.04 s快了30.91 s。

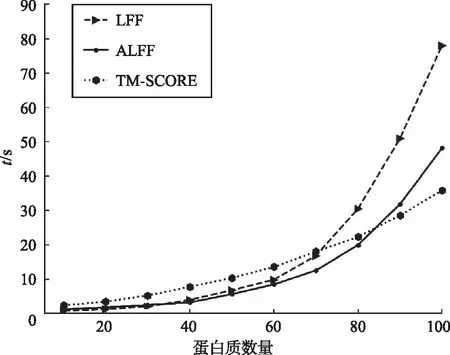
图5 LFF、ALFF和TM-score方法的计算时间比较Fig. 5 Calculation time comparison of LFF, ALFF and TM-score methods

3 结语

本文通过对LFF方法的改进得到ALFF方法，该方法可以发现蛋白质的相似性和其局部特征有非常密切的关系，利用这种关系得到的局部特征频率可以很好地表示蛋白质的结构。ALFF利用OTSU算法对数据选择合适的局部特征，MeanShift代替k-medoids做聚类分析，改进了2个重要参数的选择，避免了人工调参，相比LFF，在重构矩阵对比差异中有更低的错误率。在数据集的预处理上，ALFF去掉了冗余的等效子矩阵，缩小了接近一半的数据量，使得算法能够处理更大的数据集。相对于LFF，ALFF在蛋白质结构相似性分析的class、fold、superfamily、family的分类中有更高的一致性，分别提升了0.7、2.3、2.8、3.5个百分点。在蛋白质相似性的对比实验中，ALFF总体上和TM-score保持比较好的一致性，能够较好地计算出同源蛋白质的相似性。相比于LFF，ALFF计算所花费的时间大大降低，并且准确性有了进一步提升。但是从部分实验中发现，基于局部特征的计算方法也有一些不足之处，即当没有共同祖先的蛋白质有相同局部特征的时候也会得到较高的相似性分数，这将是今后需要研究的一个方向。