浅谈充分条件、必要条件题型的解题方法

■珠海市北京师范大学（珠海）附属高级中学 李建波

充分条件、必要条件是“常用逻辑用语”中的重点及难点，充分条件、必要条件题型在高考中也是高频率考点。因此本文例析五种常见的解题方法来处理此类题目，希望对同学们的备考能有所帮助。

一、定义法

“一般地，用p和q表示两个命题，若p⇒q，则p是q的充分条件；若q⇒p，则p是q的必要条件；若p⇔q，则p与q互为充要条件。”定义法就是借助这种推导关系来判断充分必要条件的。

例 1（2020年高考北京卷）已知α，β∈R，则“存在k∈Z使得α=kπ+（-1）kβ”是“sinα=sinβ”的（ ）。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

解析：（1）当存在k∈Z使得α=kπ+（-1）kβ时：

若k为偶数，则sinα=sin（kπ+β）=sinβ；

若k为奇数，则sinα=sin（kπ-β）=sin[ （k-1）π+π-β]=sin（π-β）=sinβ。

（2）当sinα=sinβ时，α=β+2mπ或α+β=π+2mπ，m∈Z，即α=kπ+（-1）k·β（k=2m）或α=kπ+（-1）kβ（k=2m+1），亦即存在k∈Z使得α=kπ+（-1）kβ。

综上可知，“存在k∈Z使得α=kπ+（-1）kβ”是“sinα=sinβ”的充要条件。

点评：与三角、向量有关的充要条件的判断，在分清条件和结论的基础上，必须坚持“双向推理”的原则，关键是先看由条件能否推出结论，再看由结论能否推出条件。能推出一定要说明原因，推不出一定要举出反例，只有这样才能避免出错。

二、集合法或图形法

两个命题成立的元素组成的集合（或图形）分别用p和q来表示，如果p⊆q，我们称p是q的充分条件；如果p⊇q，称p是q的必要条件；如果p=q，称p是q的充要条件。

例 2已知p：|x|≤1，|y|≤1，q：|x+y|+|x-y|≤2，则p是q的____条件。

解析：由题可知，|x|≤1，|y|≤1是以原点为中心，以边长为2的正方形内部区域（包含边界），如图1。

先讨论|x+y|+|x-y|≤2在第一象限内的情况：①当x＞0，y＞0，x≥y时，可得x≤1；②当x＞0，y＞0，x＜y时，可得x≤1，因此，在第一象限内可得到如图2所示的图像区域。

根据对称性，可以得知两个区域完全一致，因此p是q的充要条件。

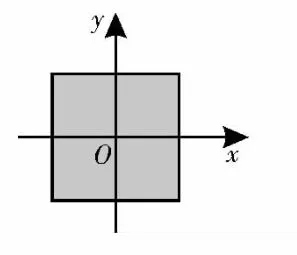
图1

图2

点评：集合或图像是一种诠释抽象数学概念的好方法，利用这种方法可以进一步加深同学们对充分必要条件概念的理解。

三、巧取反例法

在数学中，若要判定一个命题是真命题，则需要给出严谨的证明；但要判定一个命题是假命题，只需要举出一个反例即可。巧取反例法就是举出反例判断是假命题。

例 3（2020年浙江模拟）设a，b＞0，则“a＞b”是“aa＞bb”的（ ）。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

解析：若即充分性不成立；

综上可知，“a＞b”是“aa＞bb”的既不充分也不必要条件。

点评：对于很难推导出的命题，可以尝试使用巧取反例法。

四、传递性法

充分条件和必要条件都具有传递性，请看下面的例题。

例 4已知p是r的充分不必要条件，s是r的必要条件，q是s的必要条件，那么p是q的____条件。

解析：由题可得，p⇒r，r⇒s，s⇒q，所以p⇒r⇒s⇒q，故满足p是q的充分条件；但由r推导不出p，故不满足p是q的必要条件。

综上可知，p是q的充分不必要条件。

五、逆否法

原命题如果很难判断真假时，可以利用原命题与逆否命题是等价关系，判断逆否命题的真假从而达到目的。

例 5若命题p：x≠3且y≠2，命题q：x+y≠5，则p是q的____条件。

解析：p是q的什么条件等价于¬q是¬p的什么条件，由题可得¬q：x+y=5，¬p：x=3或者y=2，很显然¬q是¬p的既不充分也不必要条件，故p是q的既不充分也不必要条件。