均布径向荷载下双铰蜂窝钢拱的挠度研究

袁伟斌,许雷池

(浙江工业大学 土木工程学院，浙江 杭州 310023)

1910年， Chicago Bridge & Iron Company首先开发了蜂窝构件，与材料用量相等的实腹构件相比，前者的截面高度更高，绕强轴的惯性矩更大。腹板开孔钢拱(简称蜂窝拱)是一种新型的钢结构构件，结合了蜂窝梁和拱的特点，也开始在大跨度空间中应用开来，如航站楼、体育馆、展览馆等。蜂窝构件因其腹板孔洞的存在，其刚度沿轴长方向不再具有连续性，导致其理论分析难度陡增。早先假定蜂窝梁的结构性能和实腹梁相同，取其最薄弱空腹截面的抗弯刚度作为计算刚度[1]。但此方法误差过大且不能反映蜂窝梁的受力特点。Altfillisch等[2]较早提出了空腹桁架理论，其将蜂窝梁比拟为刚节点桁架来计算蜂窝梁的正应力和挠度。此方法至今仍为通用，后来的学者在此基础上不断改进[3-5]。随着计算机技术的发展，数值分析方法逐渐受到广泛应用。朗婷等[6]用有限元法研究了蜂窝梁的受力性能和应力分布特点。郑懿等[7]也采用有限元法对蜂窝梁的挠度影响因素进行了分析。袁伟斌等[8-10]采用能量法对蜂窝构件进行了理论研究，其中提出可将蜂窝构件当作夹层构件来进行分析。

上述的研究均是针对蜂窝直梁或柱，对于蜂窝拱的研究相对较少，目前对蜂窝拱的分析主要通过数值模拟和实验研究[11-13]，缺少理论研究。笔者借鉴文献[9]的方法，建立了蜂窝拱的总势能方程，对均布径向荷载作用下的两铰蜂窝拱的挠度公式进行了推导，并采用ABAQUS有限元软件进行了求解验证，为蜂窝拱的结构设计提供了重要的参考价值。

1 相关研究

蜂窝构件由于腹板存在孔洞，构件的刚度沿轴长方向呈现非连续性，导致不能直接使用相应的实腹计算公式。由于蜂窝构件与夹层构件受力机理相似，所以可以将蜂窝构件当作夹层构件考虑，将其上下两层连续部分作为承受弯矩和轴力的表层，中间腹板不连续部分当作承受剪力的夹层。笔者认为对于蜂窝钢拱的分析亦可采用上述方法，采用图1(a)所示的坐标系，O为拱的圆心，R为拱轴线的初始曲率半径；w为径向挠度，v为切向位移。作如下假设：1) 拱截面高度远小于初始曲率半径，则截面上的每个点的曲率半径都相同；2) 表层横截面变形后仍然保持平面，且与总轴线垂直，受弯矩和轴力作用；3) 夹层横截面上各点的切向位移沿截面高度呈线性分布，受剪力作用；4) 横向的正应变为零。

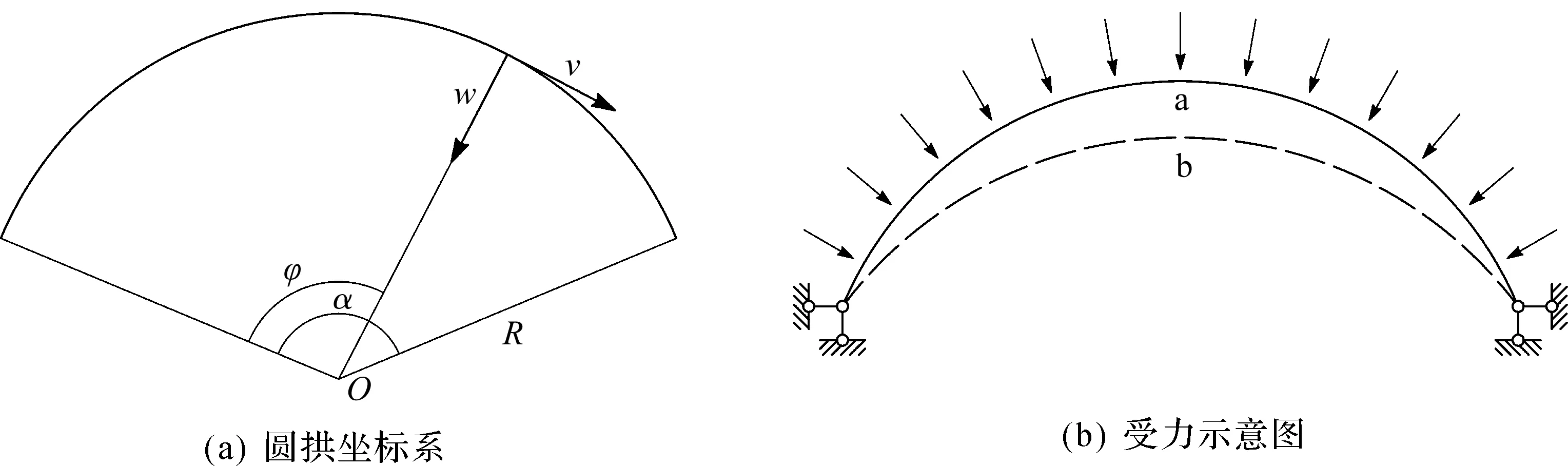
图1 结构计算简图Fig.1 The structural calculation diagram

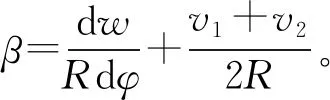
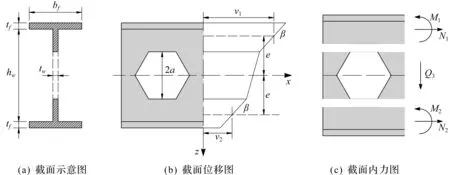
图2 截面受力状态Fig.2 The forced state of cross-section

根据图2(b)可以得到截面上任意一点(φ,z)的切向位移分别为

1) 上部T形截面，即-(hw/2+tf)≤z≤-a时，有

(1)

2) 下部T形截面，即a≤z≤(hw/2+tf)时，有

(2)

3) 中间截面，即-a≤z≤a时，有

(3)

得到的上下T形截面上任一点的切向位移公式，与文献[14]得到的拱截面上任一点的切向位移公式相同。由于假设了横向的正应变为零，所以截面上任一点的径向位移uρ=-w。接着由极坐标中的几何方程[15]得到相应的应变表达式为

1) 上部T形截面，即-(hw/2+tf)≤z≤-a时，有

(4)

2) 下部T形截面，即a≤z≤(hw/2+tf)时，有

(5)

3) 中间截面，即-a≤z≤a时，有

(6)

由应变表达式可得图2(c)截面上的内力分别为

(7)

(8)

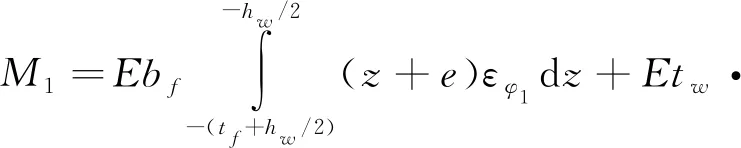
(9)

(10)

(11)

式中：E为弹性模量；G为剪切模量；Atee，Itee分别为T形截面的面积和惯性矩。

拱的应变能表达式为

(12)

式中：l为蜂窝拱的弧长；ksh为腹板不连续部分的剪切修正系数，由于截面高度远小于曲率半径，此处认为初始曲率对该系数影响可略去不计。

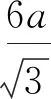
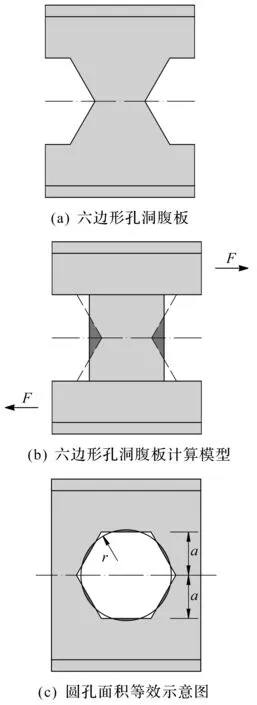
图3 腹板剪切应变能计算模型示意图Fig.3 Simple models used for calculating strain energy of web

将式(4～6)代入式(12)得

(13)

当蜂窝拱在均布径向荷载作用下时，外力做功为

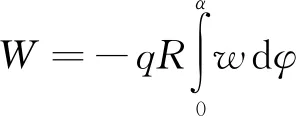
(14)

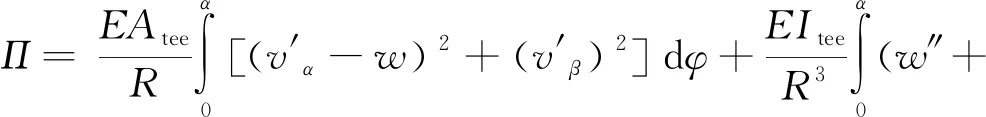
(15)

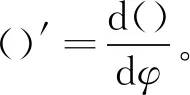
通过观察式(15)可发现第4项与第3项相似且有数量级上的差距，为简化计算可忽略第4项。如图1(b)所示，双铰支蜂窝拱在均布径向荷载下发生正对称变形，由a位置向b位置变形，设拱在均布径向荷载下的位移函数为

(16)

式中：A，B，C均为待定常数。

显然式(16)满足位移边界条件：v0(0)=v0(α)=0，w(0)=w(α)=0，w″(0)=w″(α)=0。将式(16)带入式(15)，根据最小势能原理由δΠ=0可得

(17)

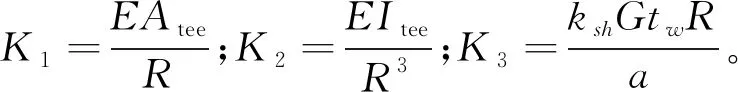
式(17)的解过于复杂，对得到的解再作简化，认为在一般工程中常用尺寸(矢跨比大于0.1)的双铰蜂窝拱在均布径向荷载下，其上下T形截面自身的弯矩M1和M2相比于轴力N1和N2产生的弯矩可忽略不计。将解略去K2，得到经简化后的径向挠度表达式为

(18)

(19)

(20)

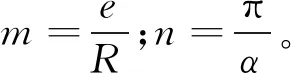
经计算分析，对于蜂窝拱常用尺寸(矢跨比在0.1～0.5)的P值一般徘徊在-0.18附近，于是由式(18)可知：对于均布径向荷载下的两铰蜂窝拱挠度的主要影响因素是蜂窝拱的初始曲率半径以及截面上下T形部分的面积。

2 有限元模型

使用ABAQUS有限元软件对均布径向荷载下的两铰蜂窝拱的正对称变形进行模拟分析。为了验证公式的适用性，对不同模型尺寸下的蜂窝拱进行了模拟，以孔洞大小、矢跨比和长细比作为变量考虑，将截面高度、板厚以及孔间距作为定值，其中长细比通过改变跨度和翼缘宽度间接考虑。采用20×20的S4R壳体单元建立模型，为了计算结果的准确性在孔洞周围加密网格分布。将端部截面耦合到形心，并限制该点的面内平动来达到铰支的边界条件，见图4。

图4 基本模型示意图Fig.4 The basic model diagram

上述模型的弹性模量E=210 GPa，泊松比ν=1/3。通过ABAQUS求得不同模型尺寸下的顶点挠度有限元值F与式(18)计算得到的理论值T分别列于表1之中。表1中所有模型的hw=180 mm，tw=10 mm，tf=10 mm，s=πr，q=10 kN/m。

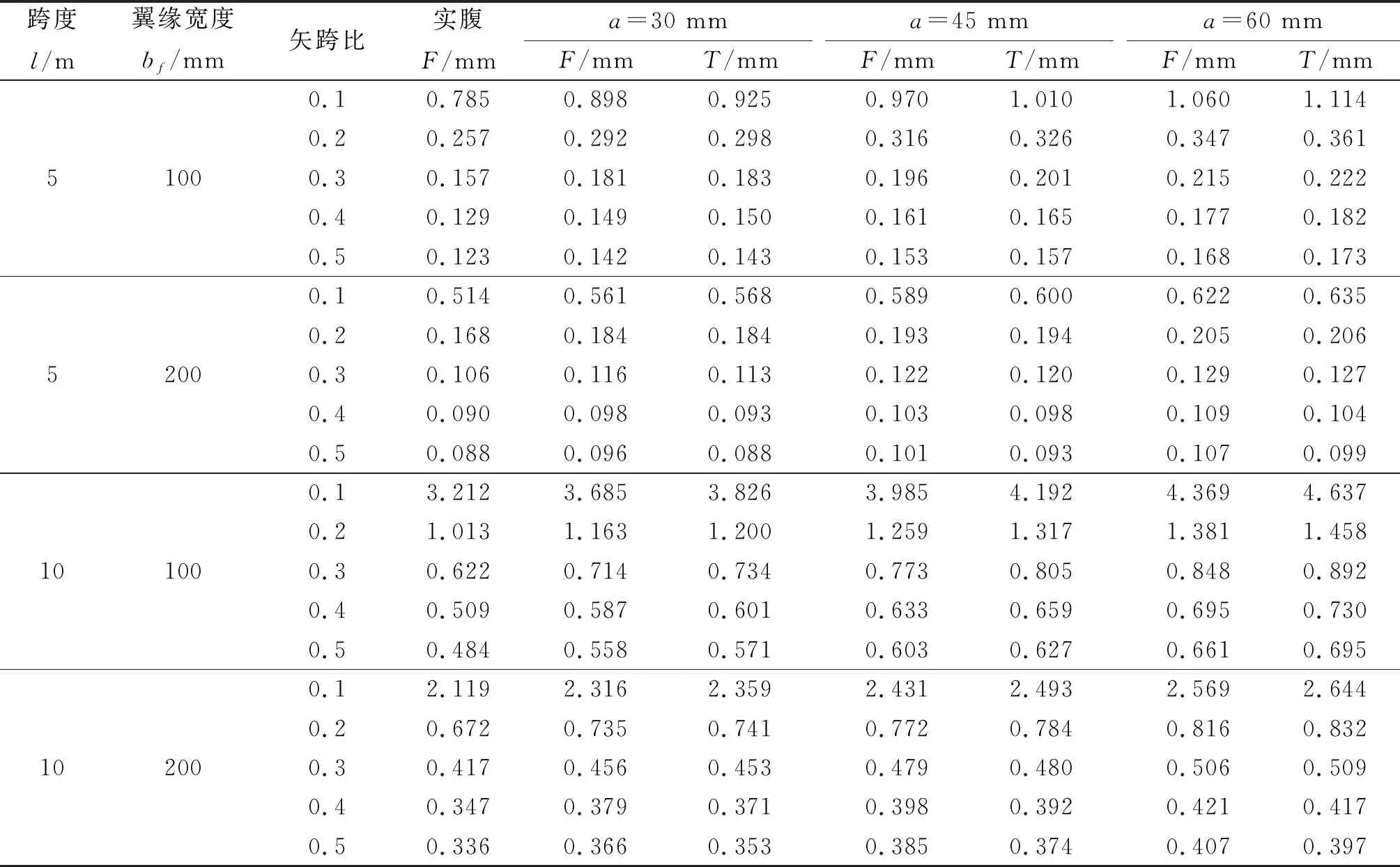
表1 不同模型尺寸下两铰蜂窝拱的顶点挠度理论解T和有限元解FTable 1 The theoretical analyses T and FEA F of two-hinged castellated steel arch beams vertex deflection with different sizes

3 分析与对比

图5，6分别为不同尺寸模型下蜂窝拱的顶点挠度示意图和理论解与有限元解对比图，结果表明：当矢跨比在0.1～0.5时，笔者提出的式(18)与有限元数据吻合较好，两者的相对误差基本在5%以内，可以满足常用尺寸的蜂窝拱的实际工程应用，也验证了笔者对蜂窝拱所采用的假设具有一定的可行性，能有效应用到对蜂窝拱的小挠度理论分析中。图6中理论解/ABAQUS解的比值随着矢跨比增大而下降，是由于较大矢跨比的双铰拱在均布径向荷载作用下，其挠曲线偏离笔者所假设的位移函数所致，但仍具有一定精度。图6还显示bf=100 mm时孔洞的大小对公式准确性的影响大于bf=200 mm时的影响，说明上下T形截面过小会放大对不连续腹板部分等效产生的误差，而对正常高宽比的截面计算分析证明笔者采用的等效缺陷并不会导致过大的误差。由图5可看出：在均布径向荷载作用下双铰蜂窝拱的孔洞越大、构件越细长，矢跨比越小，则其挠度越大；为减小蜂窝拱的挠度，参考式(18)，在跨度不变的情况下，可以采取提高矢跨比或增大上下T形截面面积的措施。

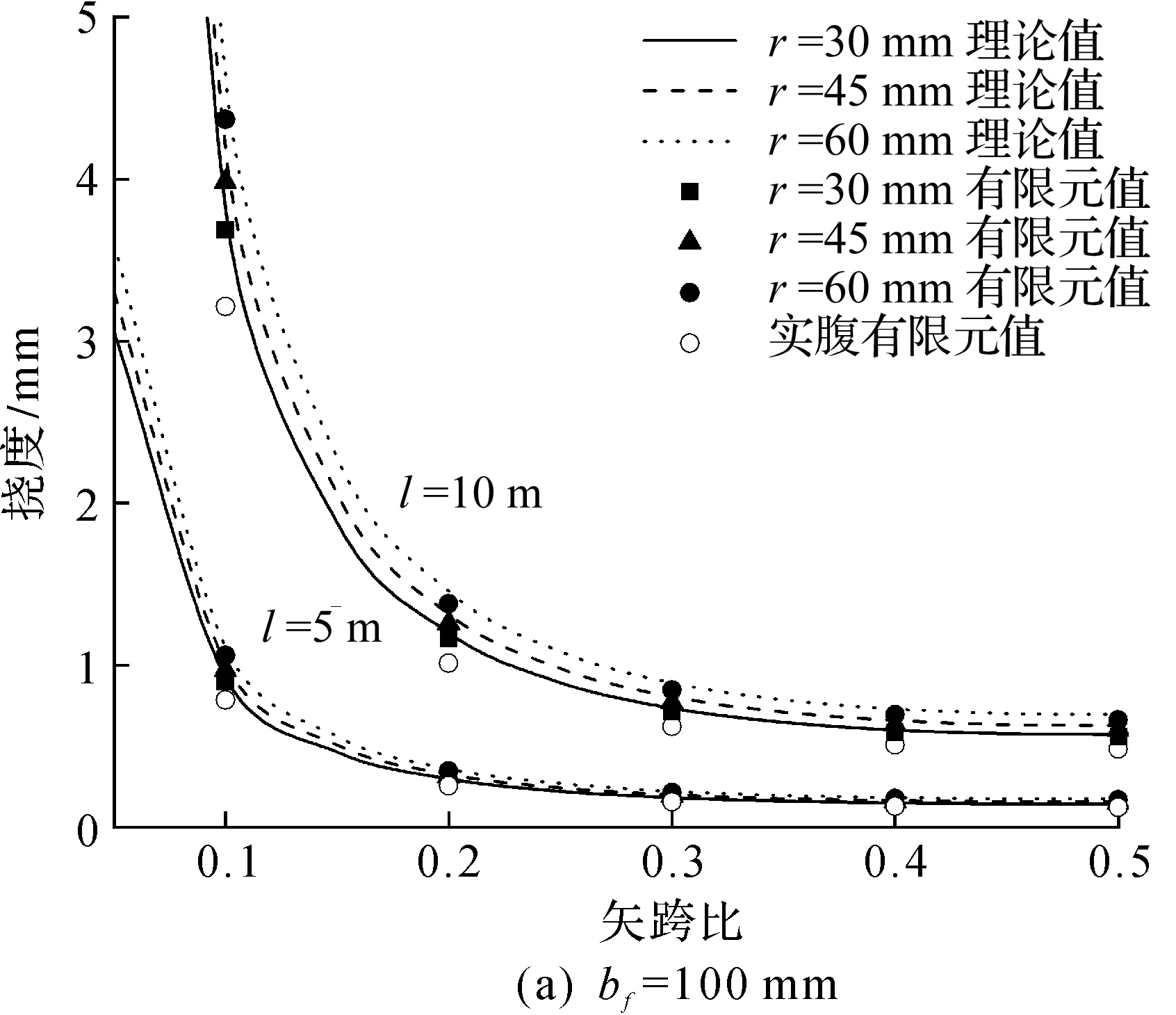
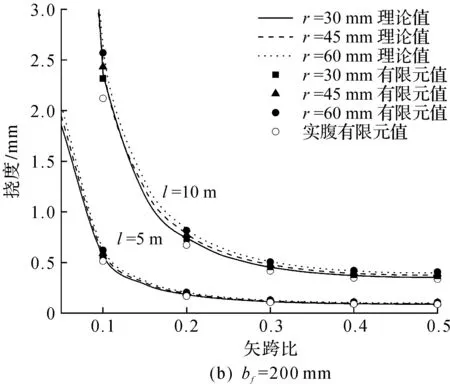
图5 不同尺寸下顶点挠度示意图Fig.5 Diagram of vertex deflection with different sizes

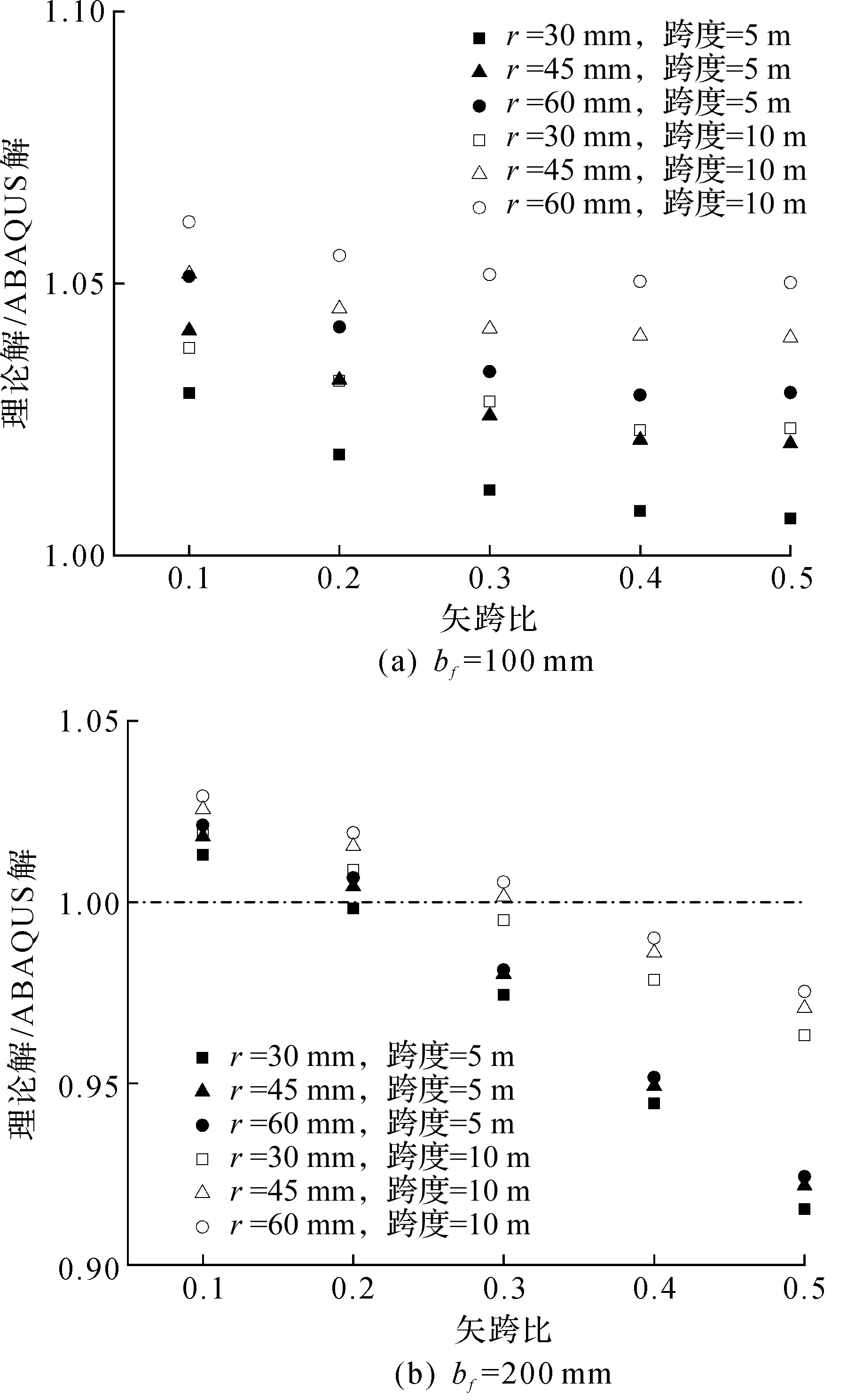
图6 理论与有限元顶点挠度对比图Fig.6 Comparison of vertex deflection between the theoretical analyses and FEA

4 结 论

对均布径向荷载下的双铰蜂窝拱的挠度进行了研究，将夹层梁理论应用到蜂窝拱中，根据最小势能原理推导了出相应的挠度公式。并采用ABAQUS有限元软件对公式的适用性进行了探讨，结果显示两者吻合较好，其精度可满足实际工程使用。同时也验证了笔者对蜂窝拱分析中所采用的一系列假设的可行性，能有效应用到蜂窝拱的小挠度理论分析中。最后，提出在跨度不变的情况下，可采取提高矢跨比或增大上下T形截面面积的措施来减小均布径向荷载作用下双铰蜂窝拱的挠度。