移动模组驱动的Tripod并联机器人建模与轨迹跟踪控制研究
徐建明,谢 丹
(浙江工业大学 信息工程学院,浙江 杭州 310023)
并联机器人的广义定义是末端执行器由几个独立的运动支链连接到基座的闭环运动链机构。广义的并联机器人的定义非常开放。现在研究较多的并联机器人可以定义为动平台和定平台通过至少两个独立的运动链相连接[1],机构具有两个或两个以上自由度,且以并联方式驱动的一种闭环机构。典型的代表有Steward平台[2]、Delta机构及其变异形式[3]等。与成熟的串联机器人相比,并联机器人是一种全新的机器人。并联机构有很多优点,其结构紧凑[4]、刚度大,使得同等质量的并联机器人负载能力更强;并联机器人的驱动机构一般装在定平台上或者接近定平台的位置,机械臂运动部分的重量较轻,因此运动速度较快,运动惯性较小,动态响应更好;又因为并联结构的特点,所以没有误差累加,精度更高[5];并联机器人在应用上与串联机器人互补,扩大了机器人的应用领域,其应用范围非常广泛[6],例如航空航天、船舶、汽车、医疗、工业等领域。在航空航天中,可以用于登月舱的起落架、自动化飞行驾驶、天线指向设备等,并联机构的高频带宽使得其非常适用于减震,可以制成主动减震器;在医疗领域,可以做微创手术和外科手术;在工业应用中,并联机器人可以装配包装,抓取分拣、定位设备等,但是并联机器人结构复杂,研究时所用的数学计算较复杂,各个关节之间具有非线性和高耦合性,因此难以实现高精度的控制[7]。
并联机器人虽然发展迅猛,但是国内针对这一方面的研究还比较少,尤其是移动模组驱动的Tripod型并联机器人。目前,主要应用于并联机器人的建模方法[8]有Lagrange法、Newton-Euler法、Kane法、Gauss法及虚功原理法等。根据是否基于机器人的动力学模型可将控制器设计分为两类,一类是只按照期望轨迹和实际轨迹的偏差进行控制,这种方法比较简单但是难以保证机器人的动态性质,常规的控制器有PID控制器、NPID控制器、模糊逻辑控制器[9];另一类是以动力学模型为基础的控制方法,如增广PD法[10]、计算力矩法[11]和Slotine提出的自适应法[12-15]等。
笔者围绕构建的Tripod并联机器人本体,首先,分析所设计移动模组驱动的Tripod并联机器人的机构构型及其移动模组和动平台的速度与加速度模型,在Tripod并联机器人各部件受力分析的基础上,采用虚功原理建立Tripod并联机器人动力学模型;其次,基于逆动力学模型和计算力矩法,研究轨迹跟踪的PID控制器设计方法;最后,考虑所设计Tripod并联机器人加工和装配误差,针对动力学模型存在参数偏差和外部干扰力的情况,采用所设计的控制器进行了轨迹跟踪控制仿真实验,结果验证了所研究控制算法的有效性。
1 模型结构分析及坐标系建立
笔者所研究的并联机器人的机器人结构由定平台、动平台、3 组平行移动模组(其中包括滚珠丝杆、滑块,3 组平行四边形连杆,每组支链通过4 个球关节连接)组成,其三维建模如图1所示,末端执行器的位置由3 组滑块移动的距离决定。

图1 Tripod并联机器人的Solidworks三维建模Fig.1 Three-dimensional modeling of tripod parallel robot with solidworks
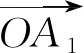
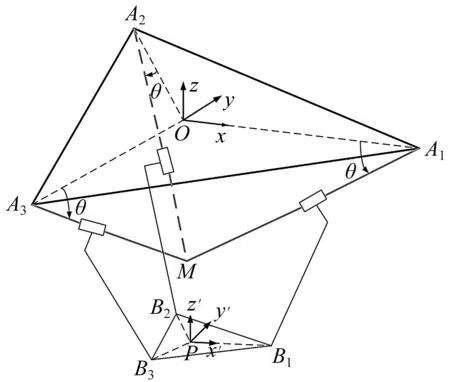
图2 Tripod并联机器人原理图Fig.2 Principle diagram of tripod parallel robot
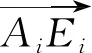

图3 单支链原理图Fig.3 Schematic diagram of single branched chain
2 动力学分析与建模
根据图3建立第i个移动模组简化支链的闭环回路方程[16]为
(1)
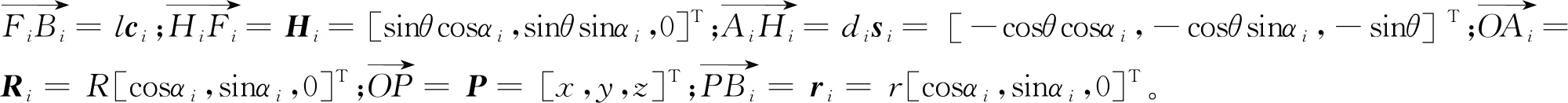
2.1 速度与加速度
2.1.1 速度模型
将式(1)化简并对时间求导,可得速度模型为
(2)
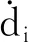
(3)
进而,得到并联机器人的雅可比矩阵为
(4)
式(4)表示了动平台速度与驱动器之间速度的转换关系,将式(2)两边同时叉乘ci,可得
(5)
由于球关节的约束,从动杆不能绕着自身的轴线转动,第i个从动杆的角速度可以表示为
(6)
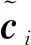
从动杆的中心速度vi为
(7)
式中Jvi为从动杆线速度与动平台速度之间的雅克比矩阵,综上可得从动杆的雅克比矩阵,即
(8)
2.1.2 加速度模型
对速度模型即式(2)两边对时间进行求导,可得加速度模型为
(9)

式(9)两边同时点乘ci,可得第i滑块的加速度计算式为
(10)
式(9)两边分别叉乘ci,可得第i个从动杆的角加速度为
(11)
对式(7)等式两边关于时间求导并整理,可得从动杆的中心加速度为
(12)
2.2 动力学模型
假设系统的各个部分都是刚性的且摩擦力可以忽略不计,利用牛顿欧拉方程对机器人各个部分进行受力分析。对动平台进行受力分析,可得
(13)
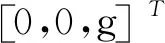
对从动杆进行受力分析可得
(14)
式中:mi为第i个从动杆的质量;fi和ni分别为作用在第i个从动杆的外力与外力矩。
由于滑块只做平移运动,没有转矩,所以对滑块进行受力分析可得
(15)
式中:mdi为第i个滑块的质量;fdi为滑块所受的外力。
对电机承受的力矩进行分析,可得
(16)

(17)
根据虚功原理[20],令整个机械臂处于平衡状态,可以得到力矩平衡方程为
(18)
式中δ为虚拟位移的变化,而且有
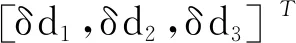
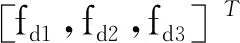
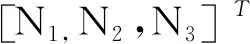
根据式(4),可得
(19)
(20)
将式(19,20)代入到式(18)中,可得
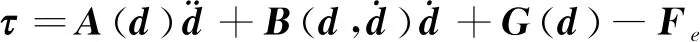
(21)
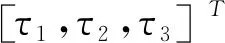
(22)
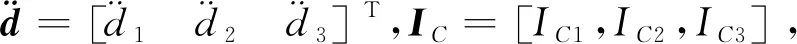
(23)
重力项为
(24)
负载项为
(25)
3 计算力矩法的PID轨迹跟踪控制算法
3.1 控制器结构与参数设计
计算力矩控制器设计[21]的基本思路是在内控制回路中引入一个非线性补偿,使机器人化为一个更易于控制的线性定常系统,笔者引入PID控制方法进行控制器的设计,所设计的系统结构框图如图4所示。

图4 计算力矩控制结构图Fig.4 Structural chart of computational torque control
对加速度补偿项引入偏置的PID控制,表达式为
(26)

根据控制系统结构图可以得到控制率的表达式为
(27)
将式(26)代入式(21)中,可得
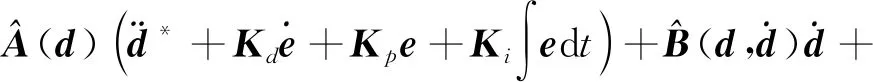
(28)
式(28)中,令
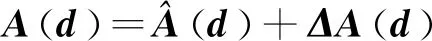
(29)

e=d*-d
(30)

(31)
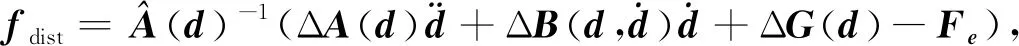
(32)
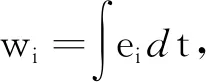
(33)
所以第i个移动模组的系统的特征方程为
(34)
对于三阶系统,特征方程可以写成
(35)
综上可得
Kdi=(2ζ+1)ωni
(36)
(37)
(38)
式中:ζ为阻尼比(介于0~1的无量纲数);ωni=[ω1,ω2,ω3]T为振动的固有频率。
3.2 仿真结果分析
根据实际需要选择合适的阻尼比和固有频率,可以得到
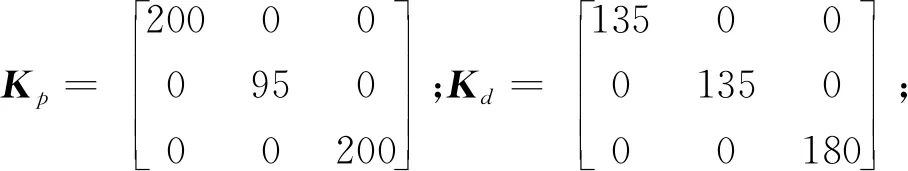
考虑存在加工误差和装配误差,以SolidWorks三维软件测量值为实际值,仿真时以估计值设计控制器,以实际值为机械臂模型参数,具体参数如表1所示。

表1 并联机器人仿真所需参数Table 1 Parallel robot simulation necessary parameters
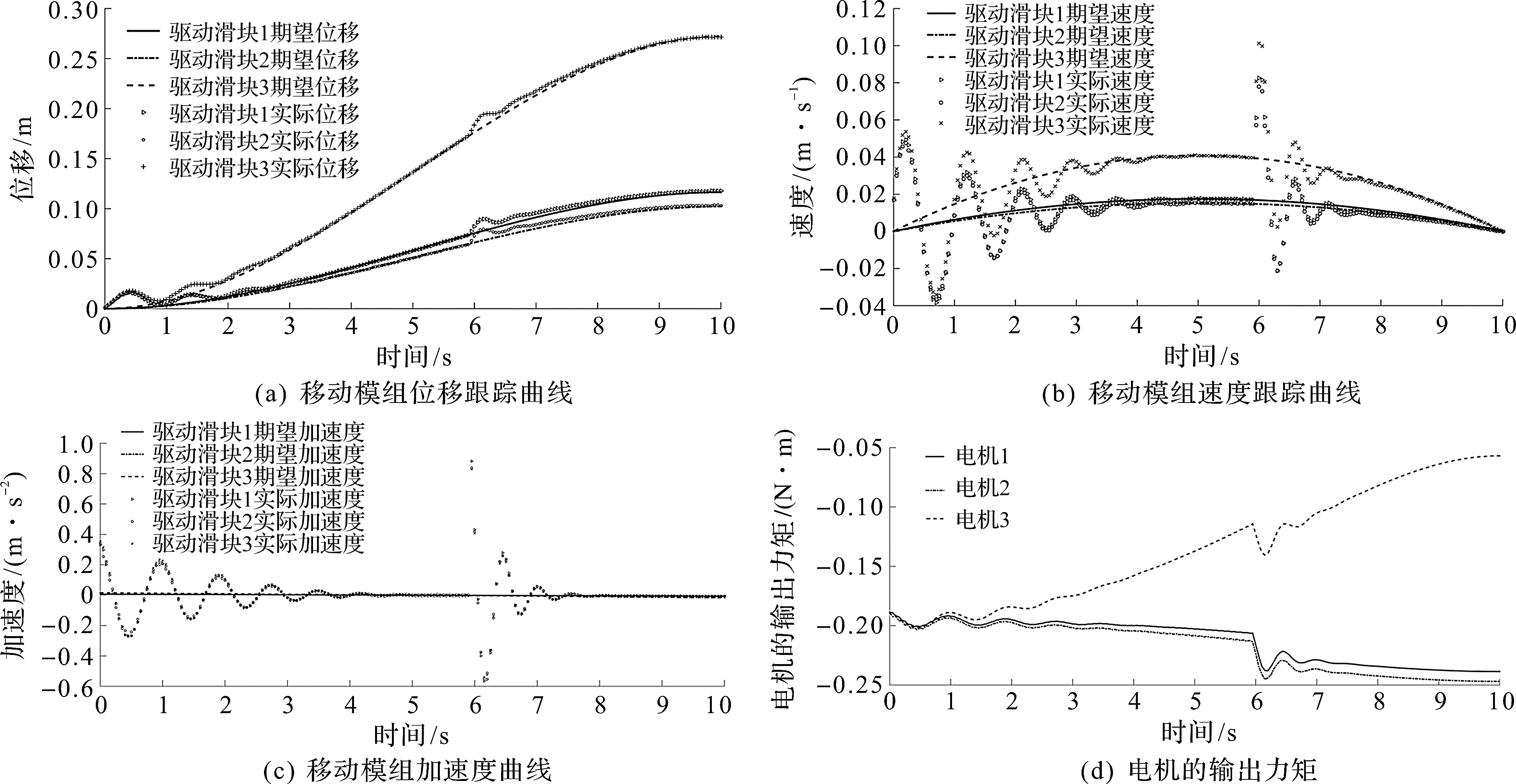
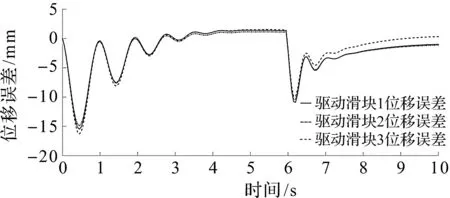
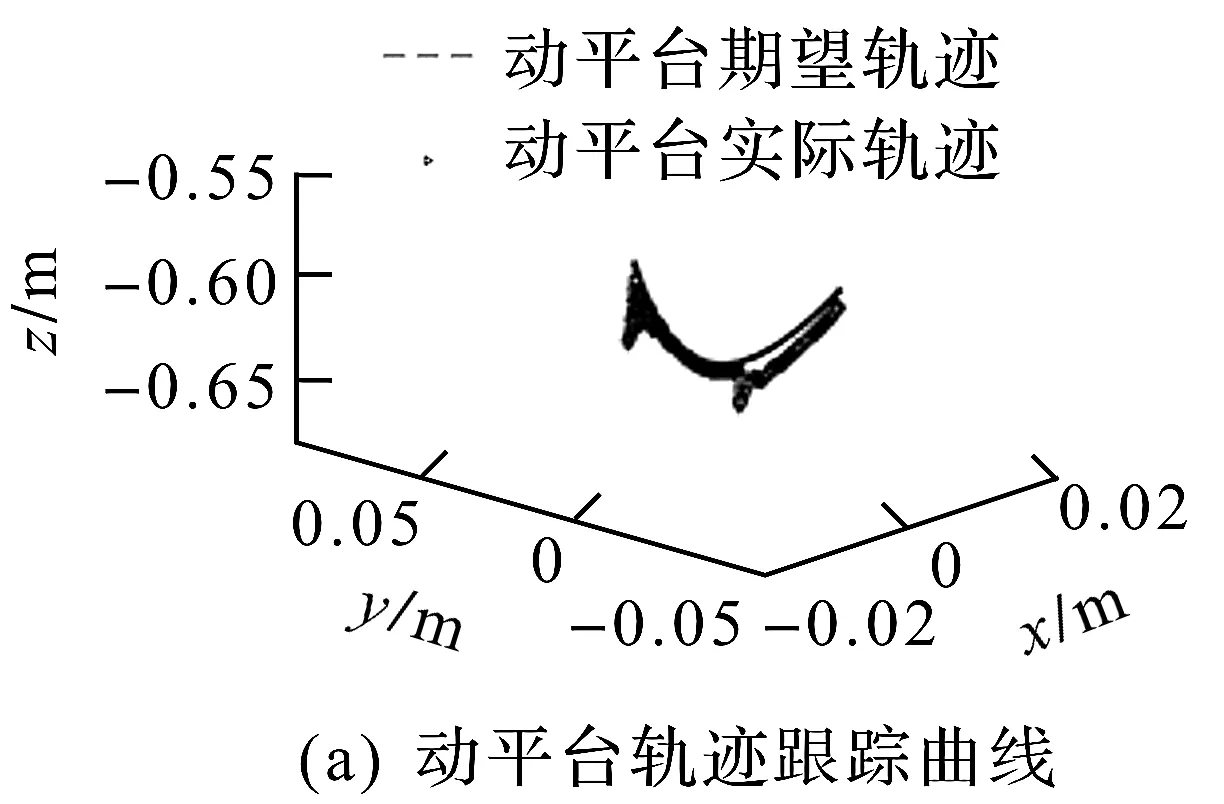
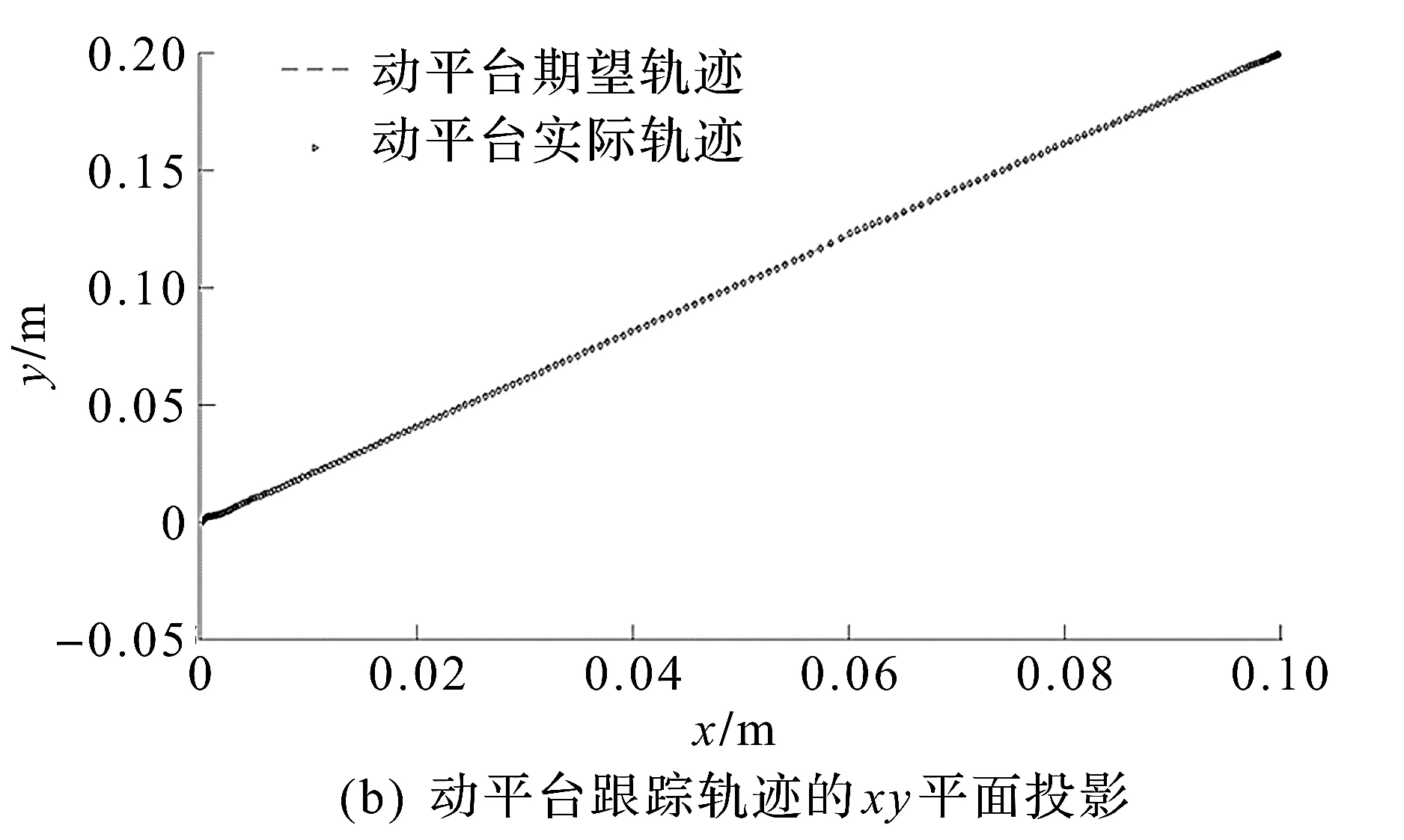
根据表1可以对新型Tripod并联机器人进行控制算法仿真,设定采样时间为0.05 s,运行时间0 (39) (40) 可以得到规划初始值和最终值之间的三次多项式[22]轨迹为 (41) 仿真时,在第6 s时加入0.05 N的阶跃型外力,3个移动模组轨迹跟踪仿真结果如图5所示。 图5 3 个移动模组轨迹跟踪效果Fig.5 Tracking effect of three moving modules 仿真过程中3 个移动模组的期望位移与实际位移的误差曲线如图6所示。 图6 3 个移动模组轨迹跟踪位置误差曲线图Fig.6 Location error curve of track tracking for three moving modules 动平台的轨迹跟踪仿真结果如图7所示。 图7 动平台轨迹跟踪曲线Fig.7 Trajectory tracking curve of moving platform 根据仿真结果,移动模组1~3的性能指标如表2所示,由仿真结果可以得出轨迹跟踪效果较好,加入外力后可以很快地恢复轨迹的跟踪,表明所研究控制算法有效。 表2 PID算法结果性能指标Table 2 Performance indicators of results of PID algorithms 研究了移动模组驱动的Tripod并联机器人建模方法以及基于计算力矩法的PID轨迹跟踪控制算法。采用Newton-Euler法对Tripod并联机器人各个移动模组及末端执行器进行受力分析,利用虚功原理建立机器人的动力学模型;基于逆动力学模型,设计了基于计算力矩的PID控制系统。针对动力学模型存在参数偏差和外部干扰力的情况,采用所设计控制器进行了轨迹跟踪控制仿真实验,结果验证了所研究控制算法的有效性。未来可以应用笔者所研究建模和控制方法在研制的移动模组驱动Tripod并联机器人上开展实验测试,进一步深入研究Tripod并联机器人建模与自适应控制方法。
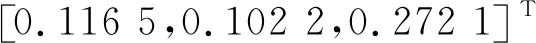
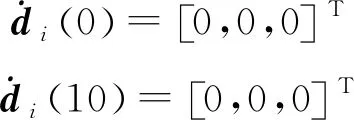


4 结 论

