基于BPNN的黄酒前酵温度控制模型与仿真

蒋美仙，王振水，吴国兴，黄苏西，郑佳美

(浙江工业大学 机械工程学院，浙江 杭州 310023)

为提高黄酒产量和品质，我国黄酒企业积极引进自动化酿造设备，逐步改进传统酿造工艺。但针对前发酵过程的温度控制至今仍没有切实有效的方法，严重制约了黄酒生产的自动化水平及黄酒品质的稳定。近年来国内外学者对啤酒以及工业注塑机的温度控制方面有相关研究，但鲜有关于黄酒温度控制的相关研究。杜锋等[1]运用模糊控制对啤酒发酵进行温度控制，提出了变论域的模糊PID控制方法；毕竞锴[2]在啤酒发酵过程智能化自动化控制过程中引入了自适应调整的模糊控制；冯絮影[3]对发酵过程进行建模并对温度控制问题进行研究，提出基于生物发酵过程的建模与控制方法；Kanagalakshmi等[4]基于注塑成型温度控制的实际需要，提出了一种基于多模态比例积分微分(PID)的实时控制方案；Nath等[5]基于传统内部模型控制(IMC)方法；李胜等[6]采用先进的模糊控制算法与传统的PID控制相结合的模糊PID控制策略，将模糊控制的鲁棒性好、适应性强以及PID控制可对控制参数进行实时调节等有效地结合起来。

通过文献分析可知：黄酒前发酵过程的温度控制主要集中在内部模型构建及控制器参数调整这两个方面。而黄酒前发酵过程温度的变化是一个高度非线性的时变过程，难以建立精确的数学模型，即使建立了模糊数学模型，其参数调节也是个难点。因此，针对黄酒前酵过程的温度控制研究，主要集中在控制器设计方面。当前工业应用较为广泛的PID控制器具有高精度、快速响应等优点，其参数调节一直是研究的关键。笔者将BP神经网络应用于PID控制器的参数调节，充分发挥BP神经网络的自学习能力，实现控制参数的自动调整。

1 问题描述

黄酒的前酵过程中由于发酵罐内酵液在酵母菌和酒曲的作用下发生着剧烈的生化反应，会释放大量的热量，而每个阶段又要保持相对应的温度以控制发酵反应的强度。

目前，黄酒发酵温度依靠操作工的经验进行控制，操作工根据发酵液的温度、发酵时间和实时温度等因素决定冷却水阀门的开度[7]。由于人工操作自身存在着诸多不确定性，使得黄酒质量的稳定性得不到保障[8]。工业生产过程中常采用PID控制器对制造系统中某一变量进行控制，但PID控制器对于不同的受控对象需要花费大量时间进行参数调试，同时PID控制器也存在被控量的超调、稳态响应时间较长的问题[9]。针对黄酒发酵过程的温度控制，需要控制器进行快速、稳定控制，一旦发酵过程的温度产生偏差，会严重影响酵母菌繁殖，进而影响黄酒品质。

由于发酵罐内外的能量交换导致的温度变化，以数学函数进行系统辨识难度较大，且不同的发酵时间点、发酵罐容积、配方、外界环境，其数学规律是不同的，所以通过物理学及数学方法寻找控制律是行不通的[10]。通过系统输出变化量的负反馈调节机制，根据系统实时变化情况，在不需知道系统内部变化规律的情况下进行有效调节。在工业过程中，负反馈调节机制的PID控制器应用较普遍，但需经历漫长的参数调节过程，对于要求精确且快速的控制过程，控制效果十分有限。

针对PID控制器参数调节问题，笔者通过BP神经网络对PID控制器进行改进，将比例、积分和微分三个控制部分设置成BP神经网络的隐含层。各层神经元之间的连接权值相当于原先PID控制器的控制参数，通过BP神经网络训练达到调节参数的目的。同时由于BP神经网络具有计算多输入、多输出的特点，可同时对控制对象的多个控制量进行控制。改进后的温控系统图如图1所示。

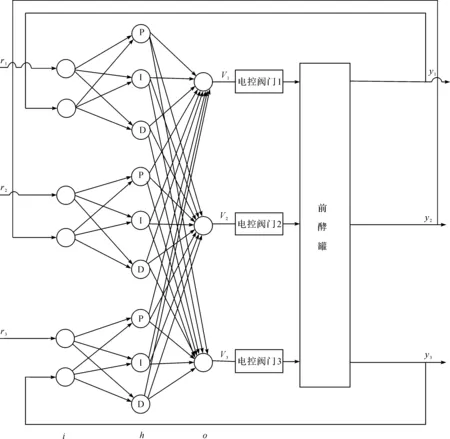
图1 前酵温控系统总体设计图Fig.1 Overall design drawing of the temperature control system of the preleaven

2 基于BPNN的黄酒前酵温度控制模型构建

神经元网络通过各神经元之间的加权和形式输出，只要神经元数量足够多、网络结构足够复杂即可实现对任意变化规律的拟合[11]。并且利用BP神经网络作为非线性组合函数，可用于多模型的输出融合[12]。神经元作为神经网络的处理单元，是神经网络最基本的组成部分，其模型结构如图2所示。

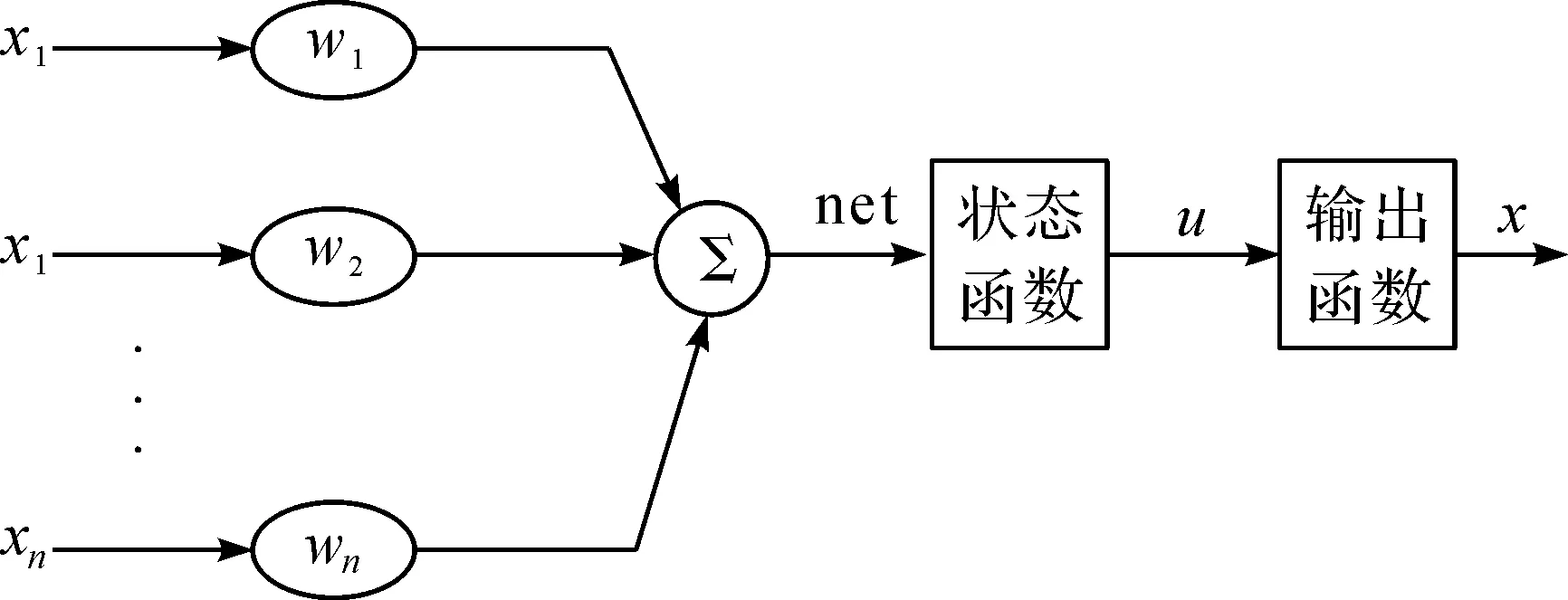
图2 神经元模型结构框图Fig.2 Structure block diagram of neuron model

神经元j的状态uj由此神经元的状态函数g决定。以神经元当前输入netj和当前状态为自变量，按其状态函数就可产生神经元的下一个状态。

神经元j的输出由此神经元的输出函数f决定。以神经元状态uj为自变量，按其输出函数就可产生神经元的输出值，即

xj(t)=f(uj(t))

(1)

神经元的输出函数也有多种形式，包括恒等函数、阈值函数、统计函数和S型函数等，笔者采用如下比例阈值函数，其数学表达式为

(2)

在控制系统的设计中，每个分支神经网络的隐含层从上到下依次划分为比例层、积分层和微分层。笔者设计的控制系统采用三分支、三输出的神经网络，现设神经元的分支序号为s(s=1,2,3)。在每个单独的分支里输入层神经元(input)的序号为i(i=1,2,3)，隐含层神经元(hidden)的序号为h(h=1,2,3)。输出层神经元(output)的序号为o(o=1,2,3)。

2.1 输入层神经元的计算

每个分支神经网络有两个输入层神经元，其输入分别为系统给定参据量和被控对象前一采样时刻的输出量，即r(k)与y(k-1)。根据改进PID控制器的设计原理，其状态变换函数go[e(k)]=e(k)，即对于任意时刻其状态是不变的，输入层神经元的状态可表示为

usi(k)=netsi(k)

(3)

2.2 比例元的计算

设v(t)为控制器的输出，e(t)为控制器的输入，kP为比例系数，则有

v(k)=gP[e(k)]=kPe(k)

(4)

比例元为s分支神经网络隐含层中的第1(h=1)个神经元，有2 个输入支路与其相连，则在任意k时刻，单元的总输入为

(5)

式中：xsi(k)为其所在的第s分支神经网络的2 个与其相连的输入层神经元的输出值；wsi1为相应的连接权值。

现统一在隐含层相关变量末尾加上标“′”，在输出层相关变量末尾加上标“″”。将输入层至隐含层连接权值当作输入层相关变量；将隐含层至输出层连接权值当作隐含层相关变量，其末尾需加上标“′”。该约定适用于全文，后文不再加以赘述。

比例元的状态函数gp为比例函数，根据改进PID控制器的要求，其比例系数应设置为1。则比例元在任意采样时刻k的状态为

(6)

因本文所有神经元是比例阈值函数，比例元的输入—输出状态曲线如图3所示。

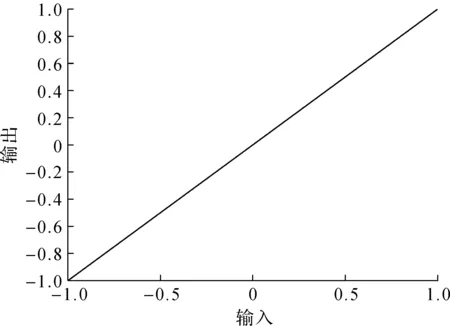
图3 比例阈值函数输入—输出状态曲线Fig.3 Proportional threshold function input-output state curve

2.3 积分元的计算

设v(t)为积分控制单元的输出，e(t)为积分控制单元的输入，TI为积分时间常数，则积分控制部分的表达式为

(7)

式中gI[e(t)]为积分函数。

在实际应用中只要采样周期足够小，就可以用累加近似代替积分。在任意采样时刻k，如果设T为采样周期，TI为积分时间常数，kI为积分系数，则积分元的计算公式为

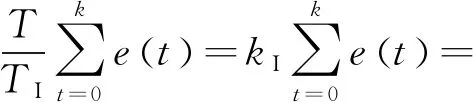
(8)

式中gI[e(k),v(k-1)]为积分函数的离散形式。

积分元为s分支神经网络隐含层的第2 (h=2)个神经元，有两个输入支路与其相连，则任意采样时刻k，单元的总输入为

(9)

式中：xsi为其所在的第s分支神经网络的2 个与其相连的输入层神经元的输出值，wsi2为相应的连接权值。

积分元的状态函数gI为积分函数，根据改进PID控制器的要求，其积分系数应设置为1。则积分元在任意采样时刻k的状态为

(10)

2.4 微分元的计算

微分控制部分的输出与输入信号的变化率成正比，同积分元的计算过程，其在采样周期足够小的情况下，可用一阶差分代替一阶微分。在任意采样时刻k，如果设T为采样周期，TD为微分时间常数，kD为微分系数，则微分控制部分的表达式为

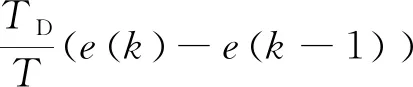
(11)

式中gD[e(k),e(k-1)]为微分函数的离散形式。

微分元为s分支神经网络隐含层的第3 (h=3)个神经元，有2 个输入支路与其相连，则任意采样时刻k，单元的总输入为

(12)

式中：xsi为其所在的第s分支神经网络的2 个与其相连的输入层神经元的输出值；wsi2为相应的连接权值。

积分元的状态函数gI为积分函数，根据改进PID控制器的要求，其积分系数应设置为1。则积分元在任意采样时刻k的状态为

(13)

微分元的输出函数也和比例、积分元的输出函数相同，同为比例阈值函数。

2.5 输出层神经元的计算

该改进控制器是三输出的，输出层有三个神经元(给其分别从上到下编号：o=1，2，3)，其输入为所有隐含层神经元的加权和，其输入为

(14)

其状转移函数和输入层神经元一样，任意时刻状态保持不变，则其状态为

(15)

2.6 连接权值的调整

对于整个控制系统，其控制性能是根据被控量的输出与系统给定参据量在对应时间序列上的偏差平方均值。由于无法得知被控对象要求的输入这一变量，如果仍以前者作为目标函数去更新连接权值是行不通的。因此将后者作为目标函数，被控对象内部也相当于神经网络的一层。为避免数据的偶然性，采用批量学习方式，每批取200 个采样点的数据，则整个神经网络的目标函数可表示为

(16)

即按梯度下降法调节神经网络的连接权值，经n步训练后，各层权重值迭代方程可表示为

(17)

式中ρ为学习步长。

隐含层至输出层连接权值调整计算式为

(18)

(19)

可求出

(20)

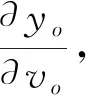
(21)

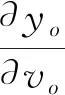
(22)

式中sgn为符号函数，用于判断自变量的正负属性。

可求出

(23)

综上所述，可得

(24)

输入层至隐含层权值调整计算式为

(25)

式中ρ为学习步长。

(26)

可得

(27)

可得

(28)

由隐含层输出函数的特性可得

(29)

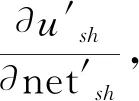
(30)

由输入输出关系可得

(31)

(32)

综上

(33)

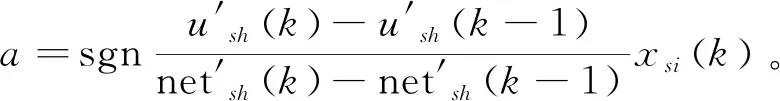
3 仿真分析

笔者设计的控制系统为典型的过程控制系统，选用Simulink软件对其进行仿真分析。Simulink是MathWorks公司开发的一个Matlab数据模型处理工具，其基于控制系统框图的设计原理，被广泛用于动态系统的建模与仿真。Simulink软件内部设计了各种API模块，可以实现多种信号的产生，信号的放大、过滤、迟延、整合与分流，信号变化的动态展示等多种功能[13]。通过仿真可以更加直观地比较传统PID控制器、改进后的PID控制器以及经过BP神经网络训练的PID控制器之间的响应速度、精度以及性能等。为了满足用户的个性化需求，Simulink软件还支持开发自定义函数，用户可根据自己的要求编写S函数，再将S函数封装成S函数模块，即实现了自定义开发API的过程。

根据温控系统的整体设计的要求，sub子模块设计如图4所示，搭建的Simulink仿真系统框图如图5所示。

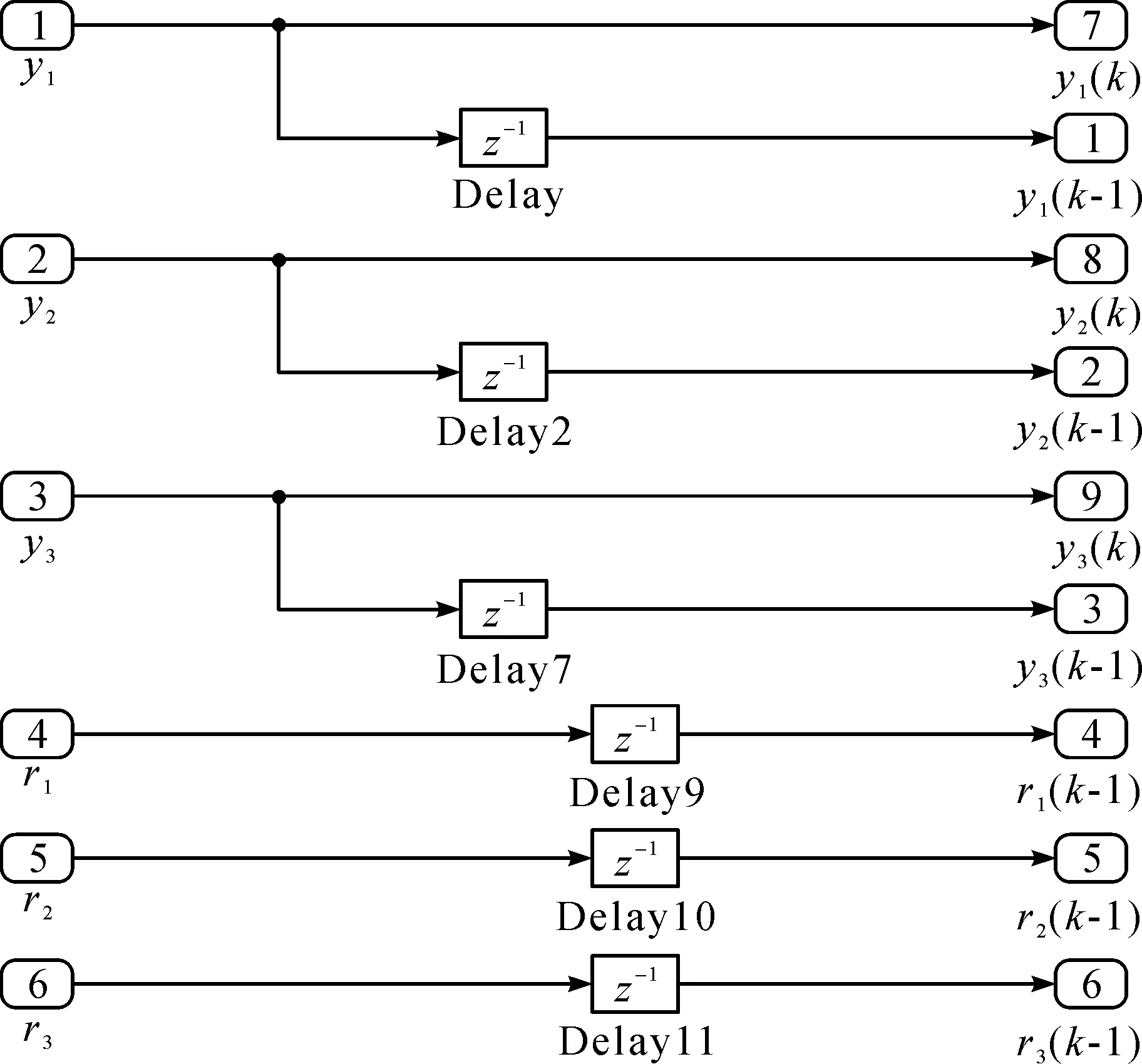
图4 输入信号处理子模块Fig.4 Input signal processing sub-module

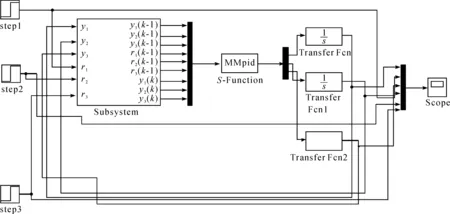
图5 温控系统仿真框图Fig.5 Simulation block diagram of temperature control system

按PID控制器控制规律，输入S函数的参数kp=0.1，ki=0.2，kd=0.3，实现连接权值初始化。其次设置隐含层至输出层、输入层至隐含层的连接权值梯度下降步长：StepLength1=0.01，StepLength2=0.01。最后对求解器的相关参数进行设置，仿真时长为200 s，固定采样步长SampleTime为0.25 s，将控制器换成传统PID控制器作为对照组，仿真结果分别如图6，7所示。

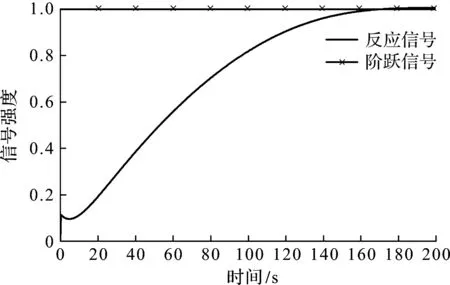
图6 未经训练的改进PID控制器的单位阶跃响应Fig.6 Unit step response of an untrained modified PID controller

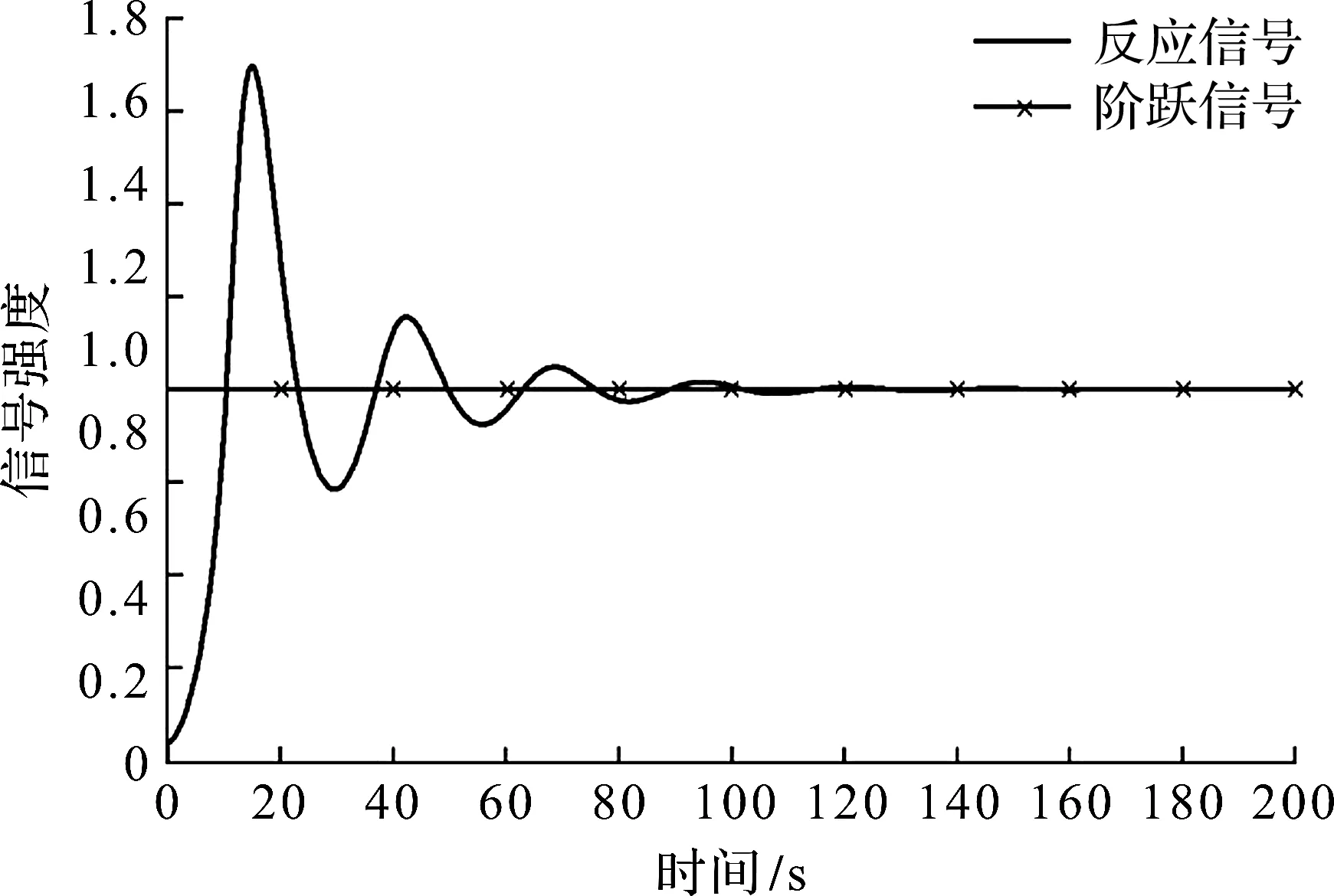
图7 传统PID控制器的单位阶跃响应Fig.7 Unit step response of traditional PID controller

神经网络模型设立200 个样本采样周期，采用每周期更新一次权值的批量学习法，分别将学习500，1 000 次后的连接权值作为初始权值进行仿真，其结果分别如图8，9所示。

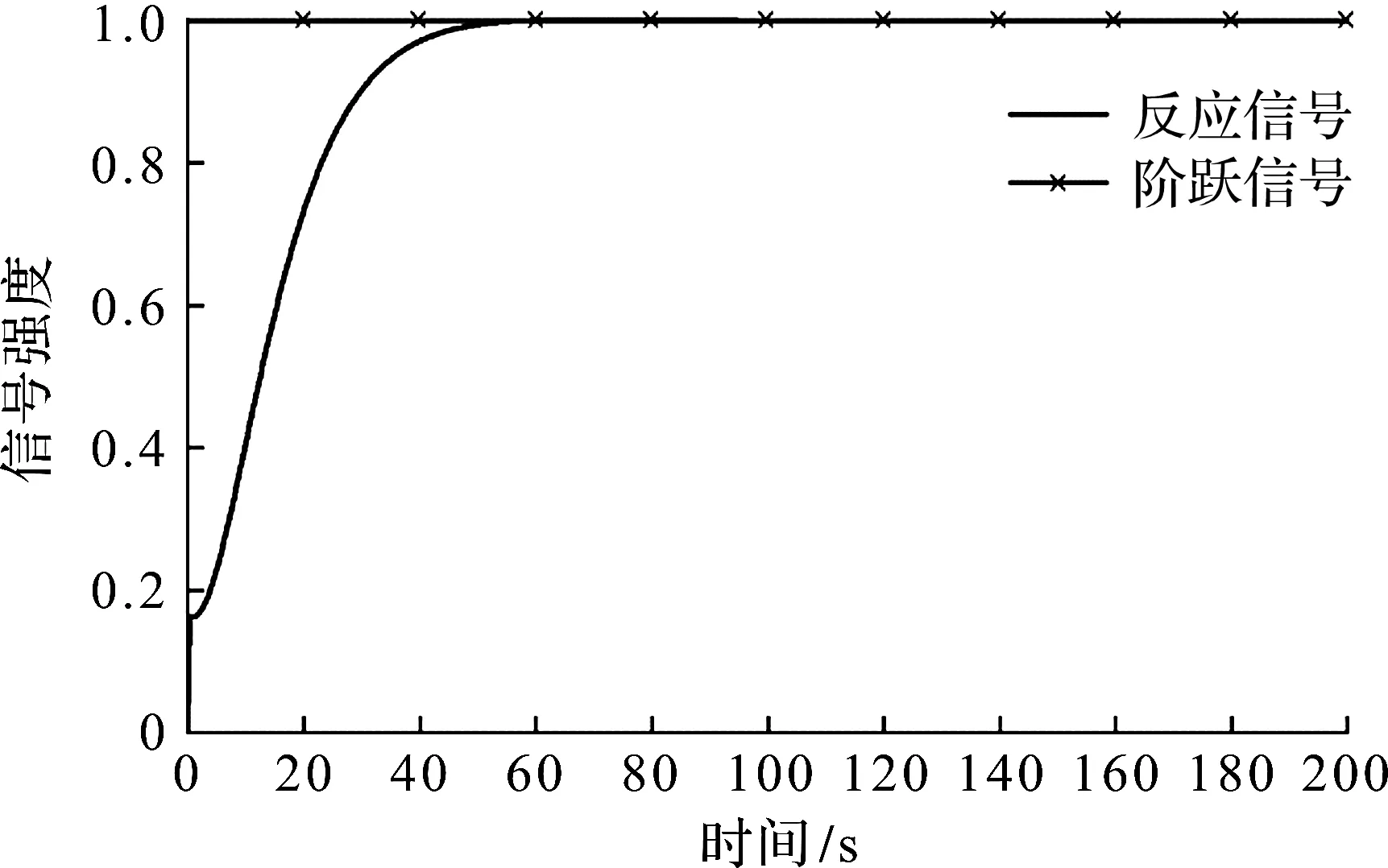
图8 训练500 次后的改进PID控制器的单位阶跃响应Fig.8 Unit step response of improved PID controller after 500 times of training

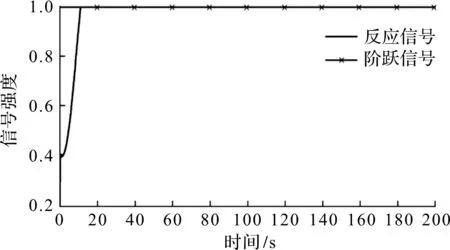
图9 训练1 000 次后的改进PID控制器的单位阶跃响应Fig.9 Unit step response of improved PID controller after 1 000 times of training

通过对比训练500，1 000 次的单位阶跃响应图曲线，得出改进的控制器经过训练次数越多，其对系统给定参据量的响应速度越快，对被控对象的控制效果越佳。

对于一个多变量控制系统，现假设黄酒前酵罐中3 个不同的测温点，分别给定不同的系统参数，研究改进控制器对多个被控对象的控制性能。3 个被控对象的系统参数，分别设定为单位阶跃、4/5单位阶跃及2/5单位阶跃，其响应如图10所示。由图10可知：3 个被控量均达到了稳态响应，因此改进后的PID控制器对多变量系统具有良好的控制效果。

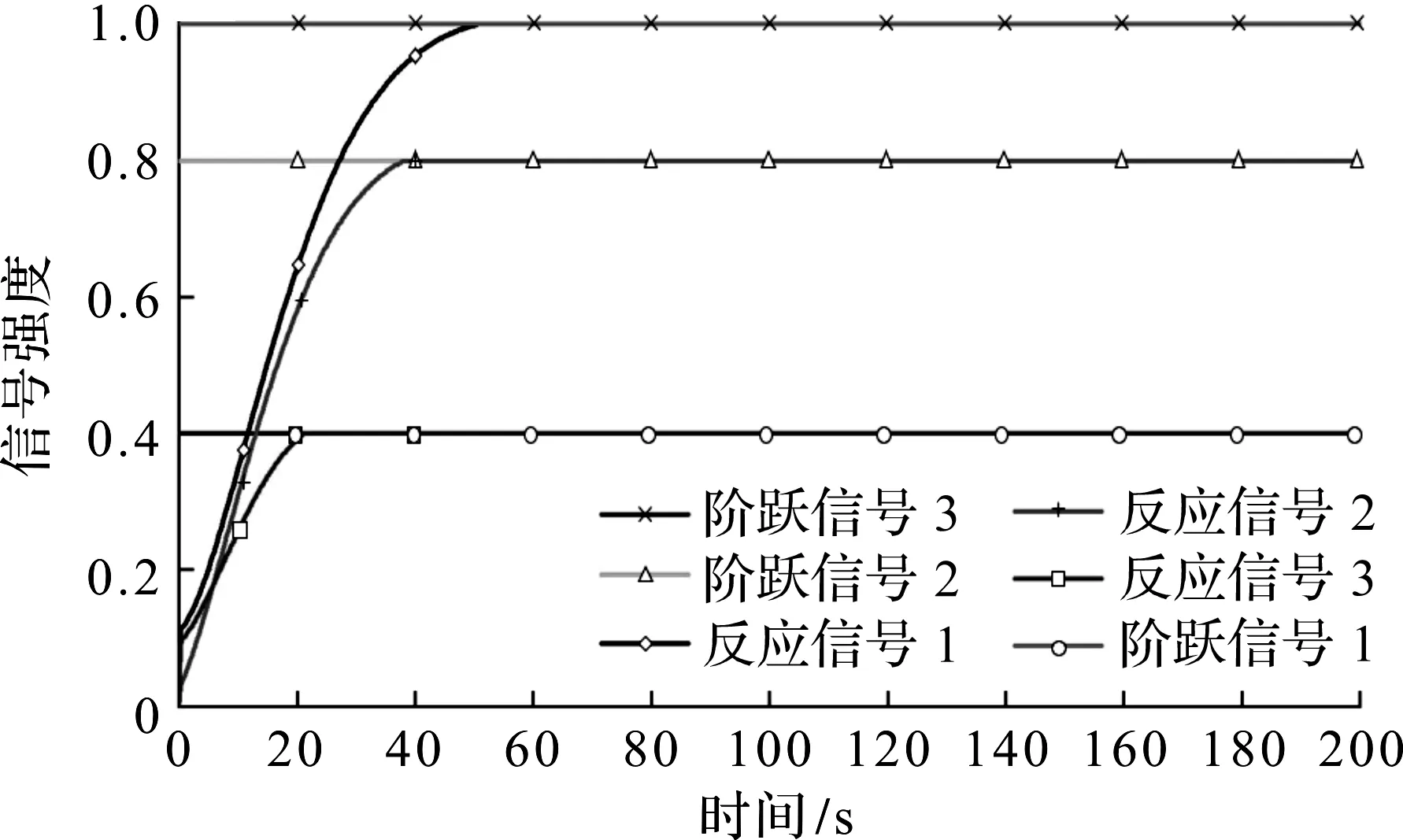
图10 改进PID控制器对多变量的阶跃响应Fig.10 Step response of improved PID controller to multivariable

4 结 论

鉴于黄酒前酵过程发酵液的温度具有强耦合、时滞性和区域差异性等复杂特性，难以建立精确的内部数学模型，而传统的控制方法难以达到理想的控制效果，故将BP神经网络应用于PID控制器的参数调节过程，对PID控制器进行了改进设计，将PID控制器的比例、积分和微分3 个控制部分分别作为神经网络的3 个隐含层节点，通过神经网络的连接权值调整实现了参数的自动调节。通过Simulink

软件进行仿真，结果表明在经历多次训练后，改进后的控制器拥有更高的精度和更良好的性能，且随着训练次数的增加，控制器的精度和性能也得到明显提高。