基于医患满意度的手术排程问题模型及算法

韩 毅，石丰源

(浙江工业大学 管理学院，浙江 杭州 310023)

在医疗市场逐渐开放，市场竞争日益激烈的时代背景下，一方面是医疗资源尤其是人力、手术室等相对不足且工作负荷不均，另一方面是随着社会的人口老龄化现象日趋严峻，患者对医疗资源的需求急速上升。医疗资源紧张的状况日益凸显，随之而来的相关问题，如医疗费用增长、医院与医生趋利行为日益严重、医患矛盾频发[1]等也都考验着我国当今医疗卫生行业的服务水平和服务质量。因此，合理的安排和利用医院的医疗资源，更好的满足患者需求，成为目前亟待解决的社会问题。

手术室作为医院的核心，在整个医院的医疗收入和支出中均占40%以上[2]，手术过程更是会涉及医院约70%的部门。因而如何通过对手术排程方案的优化，从而提高手术效率，有效缓解紧张的医疗资源，并能在提高效率的同时保证手术中各方的满意度，做到数量和质量上的双重保障，也为手术排程问题的研究者们提出了新的挑战。

1 手术排程问题文献综述

手术排程优化问题是指按照一定的排程规则，合理安排固定周期内的手术计划，计划涉及手术的时间、地点及主刀医生、手术小组、手术设备等相关因素。关于手术排程问题的研究，国外的研究者已开展了数十年之久，国内于2007年后也对手术排程及相近的车间调度等问题[3-5]逐渐加以关注，国内外近年来对手术排程问题的研究热度也都在逐年升温。在手术排程问题的提出上，有研究者如Heydari等[6]从病人的病情入手，对急诊和择期手术病人两方面因素分别加以考量；有研究者如Samudra等[7]考虑了手术过程中手术室、手术设备、医护人员等各类资源有限情况下的优化调度问题；而更多的研究者则从手术排程的优化目标如等待时间、完工时间、成本、资源利用率、满意度等着手研究。

其中Ferrand等[8]通过患者等待时间，工作人员加班时间和手术室利用率3 个性能指标，研究医院手术室的配置方案。发现将部分手术室用于紧急情况下灵活使用的方案与所有手术室完全灵活使用或者完全专用相比，在患者等待时间和工作人员加班时间上均有所改善。Lee等[9]则将日手术排程问题描述为具有模糊集的柔性车间作业模型，考虑病人的等待时间、手术室空闲时间及完工时间，通过减少患者流动的延迟，使手术完工时间最小化。Cardon等[10]在文章中指出，现有传统的手术排程方式是由外科医生与护士长协商决定，这样的安排方式既难以保证公平，又极为耗时。所以Cardon等制定了一个多目标函数，以最小化恢复床使用时间、最小化恢复阶段加班时间和最小化对病人和医生偏好的违反为目标，并以动态规划算法解决该问题。同样是关于偏好(满意度)，Penn等[11]则在排程过程中考虑外科医生对于排程计划中时间、手术室安排的偏好，并利用多准则混合整数线性规划模型快速生成手术排程的时刻表。

关于手术排程问题的研究方法，主要包括数学规划方法、仿真方法、基于启发式算法的求解方法等。其中Berg等[12]考虑门诊时间和病人出勤的不确定性，对已有的预约调度模型进行扩展，提出了一种基于两阶段随机混合整数规划的预约调度模型。Azari-Rad等[13]为提高手术室工作效率，采用离散事件仿真方法描述手术期间的过程，测试了根据患者平均住院时间安排外科医生的手术天数、按照平均持续时间和方差对手术程序进行排序、以及增加手术后病房的病床数量3 种情况对手术取消数量的影响。Fugener等[14]提出了一个将考虑范围扩大到手术下游资源(如重症监护室、患者手术结束后所需的普通病房等)的主手术调度问题，并采用模拟退火算法求得最小化的下游成本。而Tanfani等[15]则开发了一个针对主手术调度问题的两阶段算法，一阶段在所有等待的择期手术患者名单中选取可以在下一个计划周期内进行手术的患者，二阶段对患者的手术时间、手术室等做出安排。

通过对现有文献的进一步的分析可以发现，绝大多数的手术排程问题的模型构建都是以时间、成本、利用率为目标。现有的研究虽然对参与到手术过程中的医生、助理团队、患者等各方的偏好有所考量，但多数也只是将其做为约束中的一部分，极少有研究者直接把满意度视作目标加以建模。但在医患矛盾频发，强调服务质量的现状下，关于手术排程问题中各方满意度的研究更显重要。因此，笔者充分考虑手术排程涉及的各方的满意度，在多资源约束下，以最小化完成时间、最小成本、最大化治愈率和最大化医护人员、患者总满意度为目标构建模型，设计启发式算法对问题进行求解。

2 问题描述与数学模型

2.1 问题描述

手术排程以一个工作日为一个周期，一个周期内需要安排的手术数量为O，医院某科室资源包括D个医生，R间手术室和A个手术助理团队(护士小组)。每台手术分为术前准备、手术和术后恢复3 个阶段。本研究仅针对手术阶段。每台手术由一位主刀医生和一个助理小组配合完成。每一位患者都有各自的手术期望时间窗和期望的医生职称等级，每一位医生有自己对应的职称等级和对每一类手术过往的平均治愈率，每位医生与每个助理团队之间有不同的配合熟练度。配合熟练度分为4 档，依次为不默契、默契、比较默契、十分默契；医生职称也分为4 档，依次为主任医师、副主任医师、主治医师、医师。手术排程问题中包含的相关信息如图1所示。

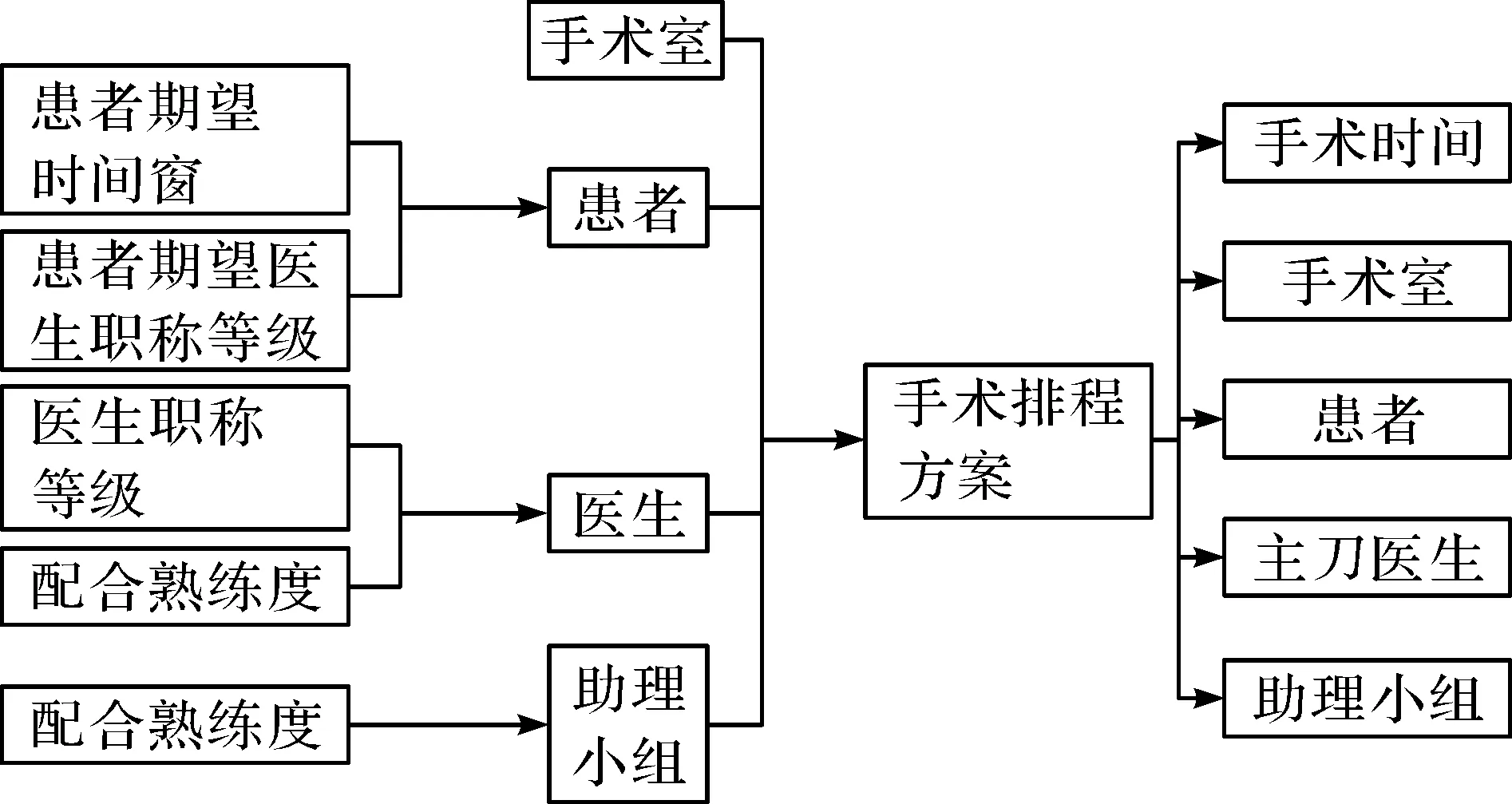
图1 手术排程问题相关信息Fig.1 Information on scheduling issues

患者的满意度与实际安排的手术开始时间和患者期望时间窗的偏离程度、实际指派医生等级和患者期望医生职称等级偏离程度有关。如某患者期望手术时间窗为12:00—14:00，则在12:00—14:00安排该患者手术时患者满意度最高，若安排患者手术时间不在时间窗内，患者满意度则线性降低，如图2所示。

图2 手术开始时刻偏离时间窗产生的患者满意度变化Fig.2 Changes in patient satisfaction at the time of surgery departure from the expected time window

如该患者期望医生职称等级为副主任医师，则安排副主任医师及以上职称的医生为该患者执行手术患者满意度最高，若安排职称在副主任医师以下的医生主刀，则患者的满意度随医生职称降低而降低。所以患者最希望在自己的期望时间窗内由满足自己期望职称等级的医生来进行手术。医护人员的满意度与医生和手术助理小组的配合熟练度有关，熟练度越高，医护人员工作中满意度就越高。所以医生最希望由与自己配合熟练度高的助理小组搭档执行手术。

最大化治愈率由安排给每位患者的医生对这类疾病以往治愈率高低决定，治愈率越高医院越满意。治愈率在0～100%，通常职称更高的医生对更多疾病拥有更高的治愈率，但也同样存在低职称医生对某种疾病治愈率更高的情况。所以尽可能由科室里对每位患者以往治愈率最高的医生主刀该患者的手术。

研究以总用时最短，总成本最低、总满意度最高和总治愈率最高做为问题的目标。其中总用时为最后一个手术的最小完成时间。总成本由手术室闲置成本，医护人员的加班成本和医生与手术助理小组间的配合成本组成，其中配合成本表现为不同默契程度造成的对手术所需材料消耗的不同。总满意度由医护人员的满意度和患者的满意度组成。

2.2 模型假设

在建模过程中对于该问题作出如下假设：

1) 一名医生一次只能处理一台手术。

2) 一间手术室一次只能进行一台手术。

3) 一个手术助理小组一次只与一名医生搭配。

4) 手术开始后不可以中途打断。

5) 手术之间优先级相同且所有手术在工作时间开始后均可操作。

6) 各资源数量已知且助手团队的数量不少于主刀医生数量。

7) 不同手术助理小组的加班成本相同。

8) 职称更高的医生对更多疾病拥有更高治愈率，但也存在较低职称医生对某种病的治愈率更高的情况。

9) 手术时长与医生和助理小组的默契程度有关，十分默契时为预计时间的90%，比较默契时为预计时间的95%，默契时为预计时间的100%，不默契时为预计时间的110%。

10) 相同默契度等级的医生和助理小组配合，完成手术的配合熟练度成本相同。

2.3 模型参数设置

为方便描述问题，定义以下参数：

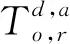
2.4 模型构建

根据上述手术排程问题的描述及参数设置，可构建手术排程模型为

F=G1+G2+G3+G4

式中：

G1=minmaxo∈OETo

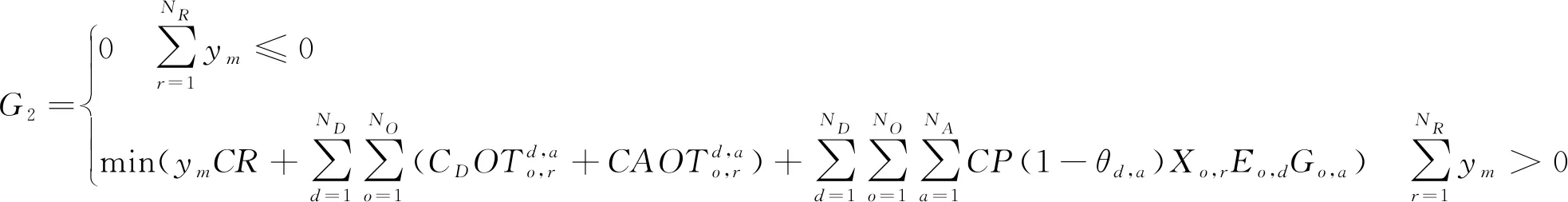
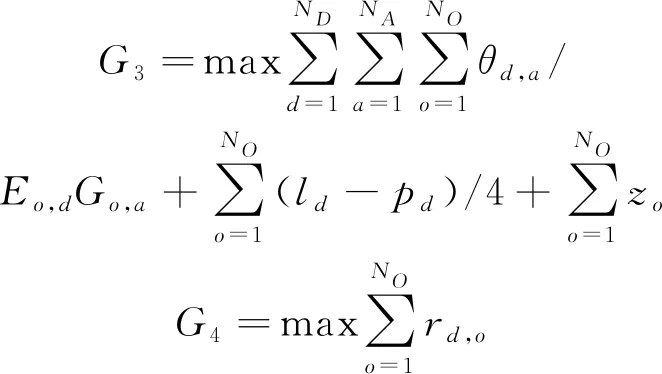
其中：目标函数G1表示最小化最后一个手术完成时间，即总用时最短；目标函数G2表示最小手术室闲置成本、医生加班成本和医生与手术助理小组配合成本之和，即总成本最低；目标函数G3表示医护人员满意度，患者满意度之和，即总满意度最高；目标函数G4表示预计的总治愈率最高。模型满足以下约束条件：

(1)

TS≤STo,r

(2)

ETo,r≤TE

(3)

Trm+LTrm≤TE-TS

(4)

(5)

(6)

(7)

(8)

(9)

(10)

0≤rd,o≤1

(11)

关于约束条件说明如下：

1) 手术结束时间由该阶段开始时间和该阶段所用时间决定。

2) 所有手术室的手术开始时间晚于一天工作的开始时间。

3) 所有手术室的手术结束时间早于一天工作的结束时间。

4) 手术室开放时间在一天的工作时间之内。

5)ym为在手术室r最后一台手术的完成时间与手术室r的常规开放时间的差值。

6) 加班手术是手术结束时刻晚于手术室常规开放时间结束时刻的手术。

7) 手术室r内若存在加班，则加班时间等于所有在该手术室加班时间开始后还未结束的手术用时之和。

8) 每台手术由一个医生主刀完成。

9) 每台手术分配在一个手术室。

10) 每台手术由一个手术助理小组与医生配合进行。

11) 医生d对手术o的治愈率为0～100%。

2.5 单目标化

利用加权系数法对4 个无量纲的子目标进行加权，处理结果为

式中：G1max,G2max,G3max,G4max分别为目标G1,G2,G3,G4在当前迭代情况下的最大值，G1min,G2min,G3min,G4min分别为目标G1,G2,G3,G4在当前迭代情况下的最小值。w1,w2,w3,w4分别为目标G1,G2,G3,G4的权系数。

3 基于启发式算法的模型求解

由于模型较为复杂，涉及的变量较多，对每台手术作出时间安排的同时还需考虑对应手术室、医生、助理团队的安排，且任意一台手术的顺序变化不但影响其他手术的顺序，其他手术的医生、助理团队和手术时间也均会随该手术的医生、助理团队的变化而发生变化。所以笔者考虑采用启发式算法对模型进行求解，并提出启发式算法的排程规则及算法流程。

3.1 算法思路

医院某科室有m间手术室，现将挑选出的手术序号及该手术对应的医生、助理小组序号和预计手术时长作为一组信息按手术室顺序依次放入1～m号手术室，如图3所示。

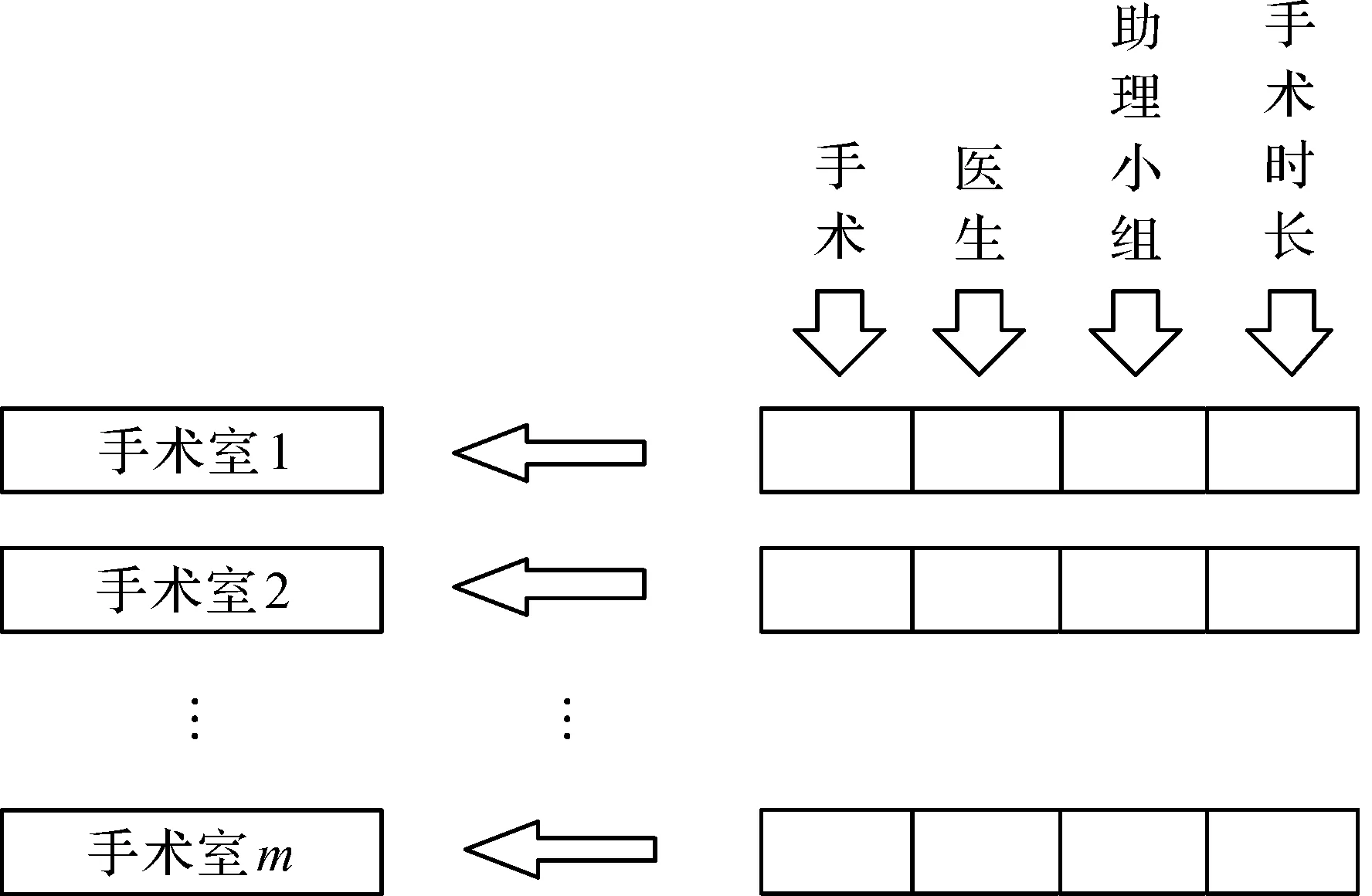
图3 将手术及对应信息依次放入手术室Fig.3 Put the operation and corresponding information into the operating room successively

所有手术室排满后，当某间手术室内手术结束时，立刻将该结束的手术及其对应的医生、助理小组等信息移出该手术室，并挑选新的手术及对应医生、助理小组和预计手术时间等信息放入该手术室，如图4所示。

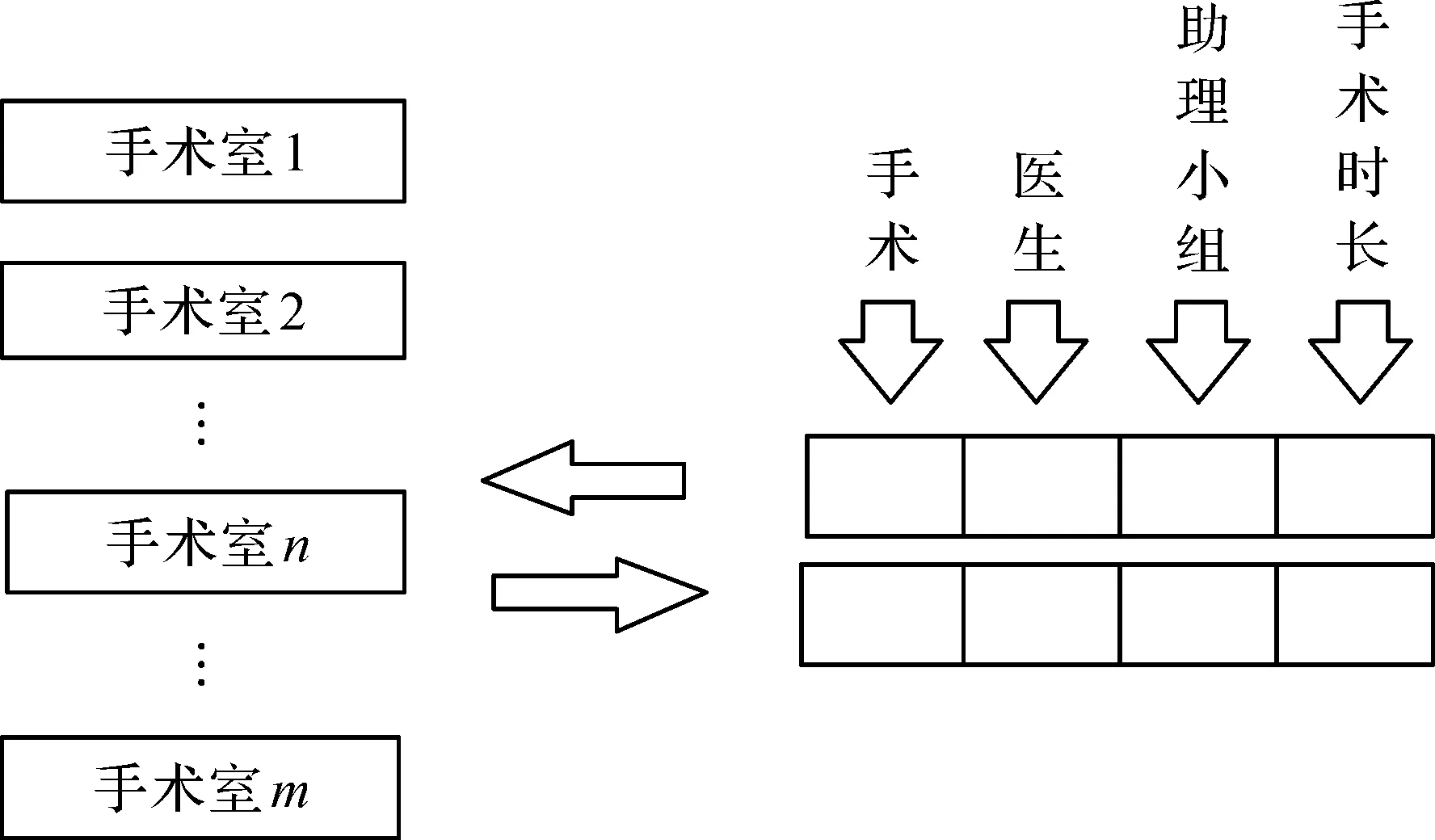
图4 新手术替换完成的手术Fig.4 New operation replaces the completed one

按上述方式，始终保持所有手术室内都在开展手术，每出现手术结束的手术室时就移出该手术室原有人员组合并在该手术室内添加新手术，直到该工作日内所有手术都安排完毕为止。

3.2 排程规则

对于手术排入手术室的先后顺序及对每一台手术对应的医生、助理小组的选择，考虑参与到手术中的各方(患者、医生、助理小组、医院)偏好，提出排程规则为

规则1基于患者偏好(病人期望手术时间窗)安排手术顺序。

优先安排期望时间窗包含当前时刻(当前时刻即手术室内上一台手术结束时间，也是下一台手术开始时间)的手术，并在其中优先安排预计手术时间最长的手术；若剩余手术时间窗均不包含当前时刻，则在剩余手术中优先安排预计时间最长的手术，规则1挑选流程如图5所示。

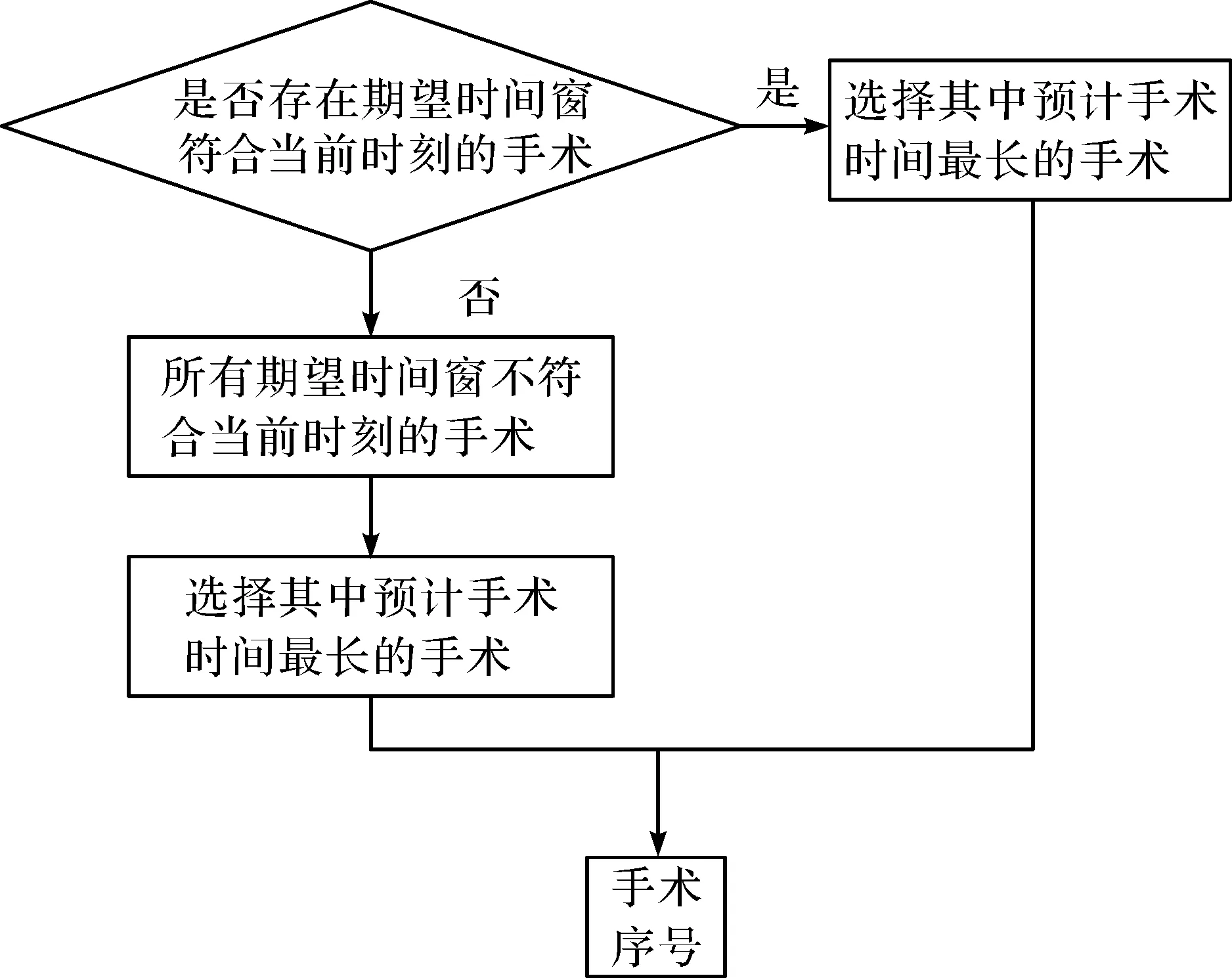
图5 手术挑选流程Fig.5 Surgical selection process

规则2基于患者偏好(病人期望医生职称等级)及医院偏好(医生对此类手术以往治愈率)为手术安排医生。

优先安排当前空闲医生中职称等级高于病人期望等级的，并挑选其中对该病人治愈率最高的医生主刀；若当前空闲医生职称等级均低于病人期望等级，则挑选其中治愈率最高的医生主刀，规则2挑选流程如图6所示。

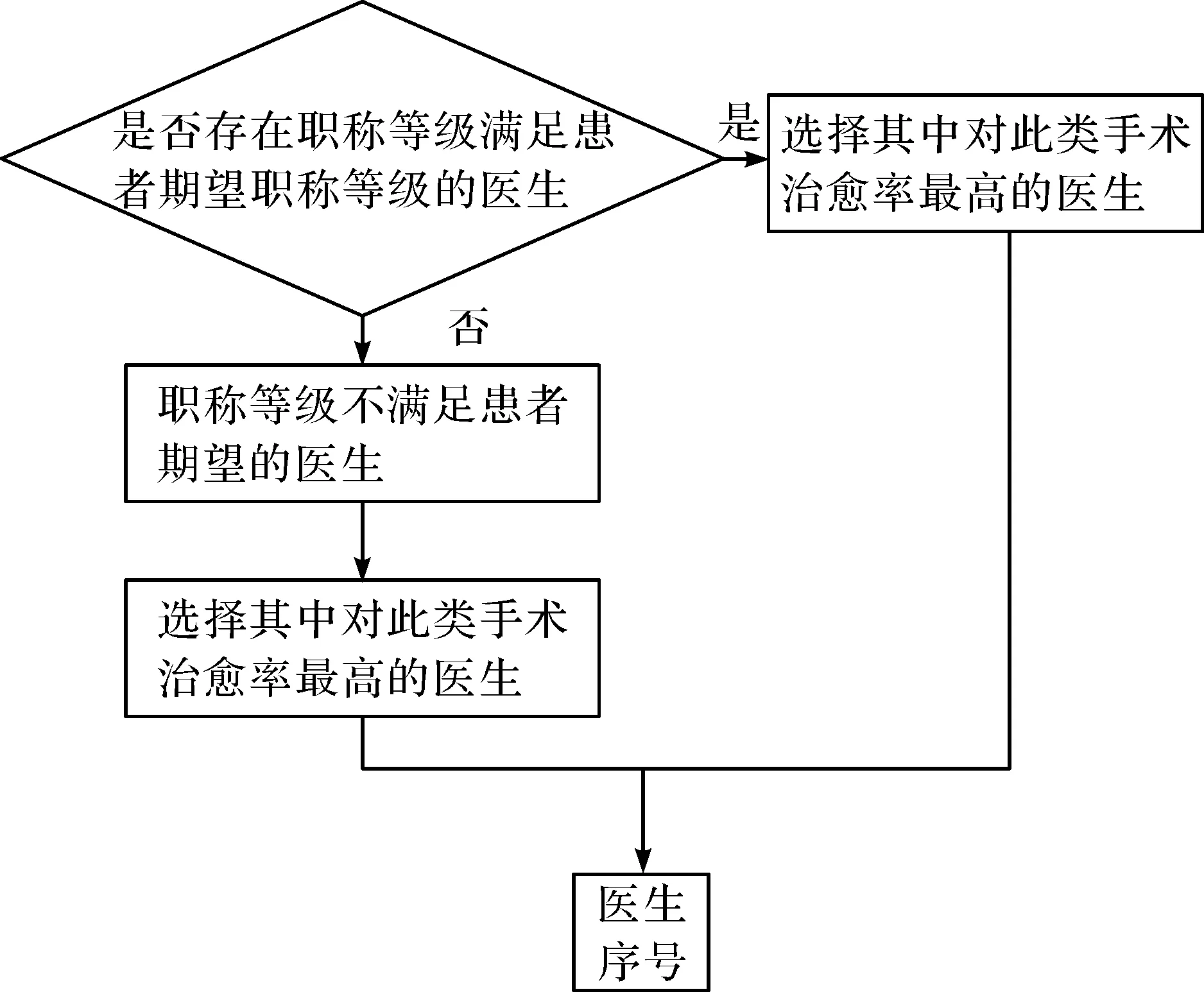
图6 医生挑选流程Fig.6 Doctor selection process

规则3基于医生及助理团队偏好(配合熟练度)为手术安排助理小组。

优先安排当前空闲手术助理小组中与该手术主刀医生配合熟练度最高的手术助理小组。

3.3 启发式算法流程

步骤1根据排程规则1挑选手术。

步骤2根据排程规则2为该手术安排医生。

步骤3根据排程规则3为该手术安排助理团队。

步骤4计算该病人手术时间，根据医生和助理团队的配合熟练度，以及预计手术时间计算。

步骤5将步骤1～4中挑选出的手术及其对应医生、助理小组、预计手术时长的信息放入第一间手术室。

步骤6对第二间到最后一间手术室安排手术，手术、医生、助理团队、手术时长按步骤1～4挑选、计算。

步骤7所有手术室都安排满时，等待到第一间空闲手术室出现(此时该手术室前一台手术结束)，移出结束的手术及对应信息，并对该手术室重新安排手术，手术、医生、助理团队、手术时长按步骤1～4挑选和计算。

步骤8重复步骤7，直到所有手术均安排完成时，算法终止。

启发式计算法流程如图7所示。

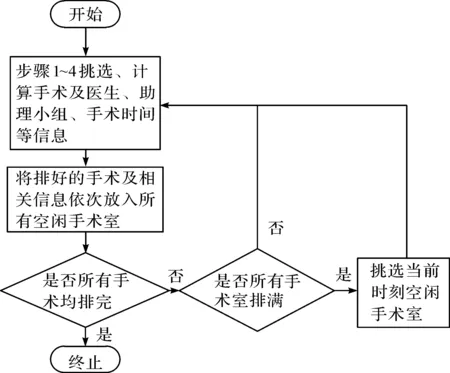
图7 启发式算法流程Fig.7 Heuristic algorithm flow

3.4 改进启发式算法

按照上述启发式算法排程，会发现职称、治愈率较高的医生可能会不断的、无休息的被安排手术，而与职称、治愈率较高的医生配合熟练度较高的助理团队也可能会面临同样的状况。这显然是不符合实际情况的，为了避免此类情况的发生，对上述启发式算法做出改进，增加排程规则4。

规则4选择医生和助理团队时，不把该手术室刚结束手术的医生和助理团队立刻再次安排进该手术室执行手术。

基于规则4改进后的算法步骤为

步骤1根据排程规则1挑选手术。

步骤2根据排程规则2为该手术安排医生。

步骤3根据排程规则3为该手术安排助理团队。

步骤4计算该病人手术时间，根据医生和助理团队的配合熟练度，以及预计手术时间计算。

步骤5将步骤1～4中挑选出的手术及其对应医生、助理小组、预计手术时长的信息放入第一间手术室。

步骤6对第二间到最后一间手术室依次安排手术，手术、医生、助理团队、手术时长按步骤1～4挑选和计算。

步骤7所有手术室都安排满时，等待到第一间空闲手术室出现(此时该手术室前一台手术结束)，对该手术室安排手术，手术按步骤1选取。

步骤8根据排程规则2，排程规则4对该手术安排医生；根据排程规则3，排程规则4对该手术安排助理团队；根据医生和助理团队的配合熟练度，以及预计手术时间计算。

步骤9重复步骤7，8，直到所有手术均安排完成，算法终止。

改进启发式计算法流程如图8所示。

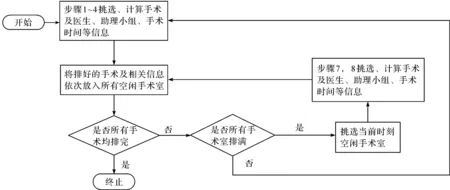
图8 改进启发式算法流程Fig.8 Improved heuristic algorithm flow

4 数值算例及分析

为检验上述模型及算法的优化效果，结合某三甲医院的手术数据设计算例如下：医院某科室有医生6 名，手术助理团队6 个，无差别手术室4 间，该工作日内需安排的手术40 例。手术室的正常开放时间为8：00—18：00，最大加班时长到24：00。一天工作的开始和结束时间即手术室最大开放时间，分别为8：00和24：00。患者的期望时间窗分为3 段，分别为8：00—11：00，11：00—14：00，14：00—18：00。6 名医生中包括1 名主任医师，1 名副主任医师，2 名主治医师和2 名普通医师。医生单位加班成本按职称依次为10，9，8，7 元/min，手术助理团队单位加班成本均为10 元/min，每分钟配合熟练度系数为1。

医生与手术助理小组配合熟练度不同对手术的影响为：以熟练度为默契的情况下手术时长为预计时长，熟练度为十分默契时，手术时长为预计时长的90%；熟练度为比较默契时，手术时长为预计时长的95%；熟练度为不默契时，手术时长为预计时长的110%。其中配合熟练度等级25%，50%，75%，100%分别表示不默契，默契，比较默契，十分默契；医生级别1，2，3，4分别为主任医师、副主任医师、主治医师、医师。每位医生对每一类手术以往的平均治愈率在0%～100%之间。医生与手术小组配合熟练度系数如表1所示。

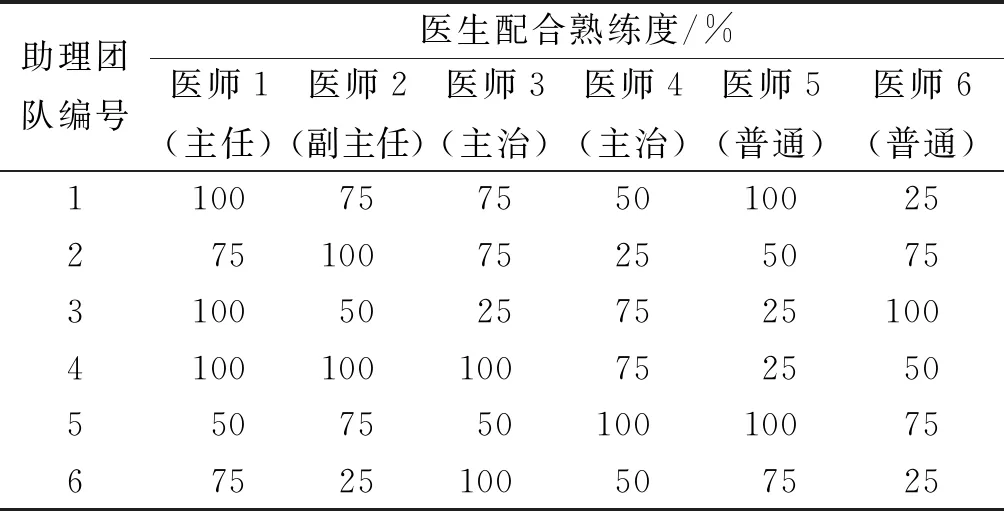
表1 医生与手术助理小组的配合熟练度

每位患者手术预计手术时间、期望医生等级、期望时间窗如表2所示。

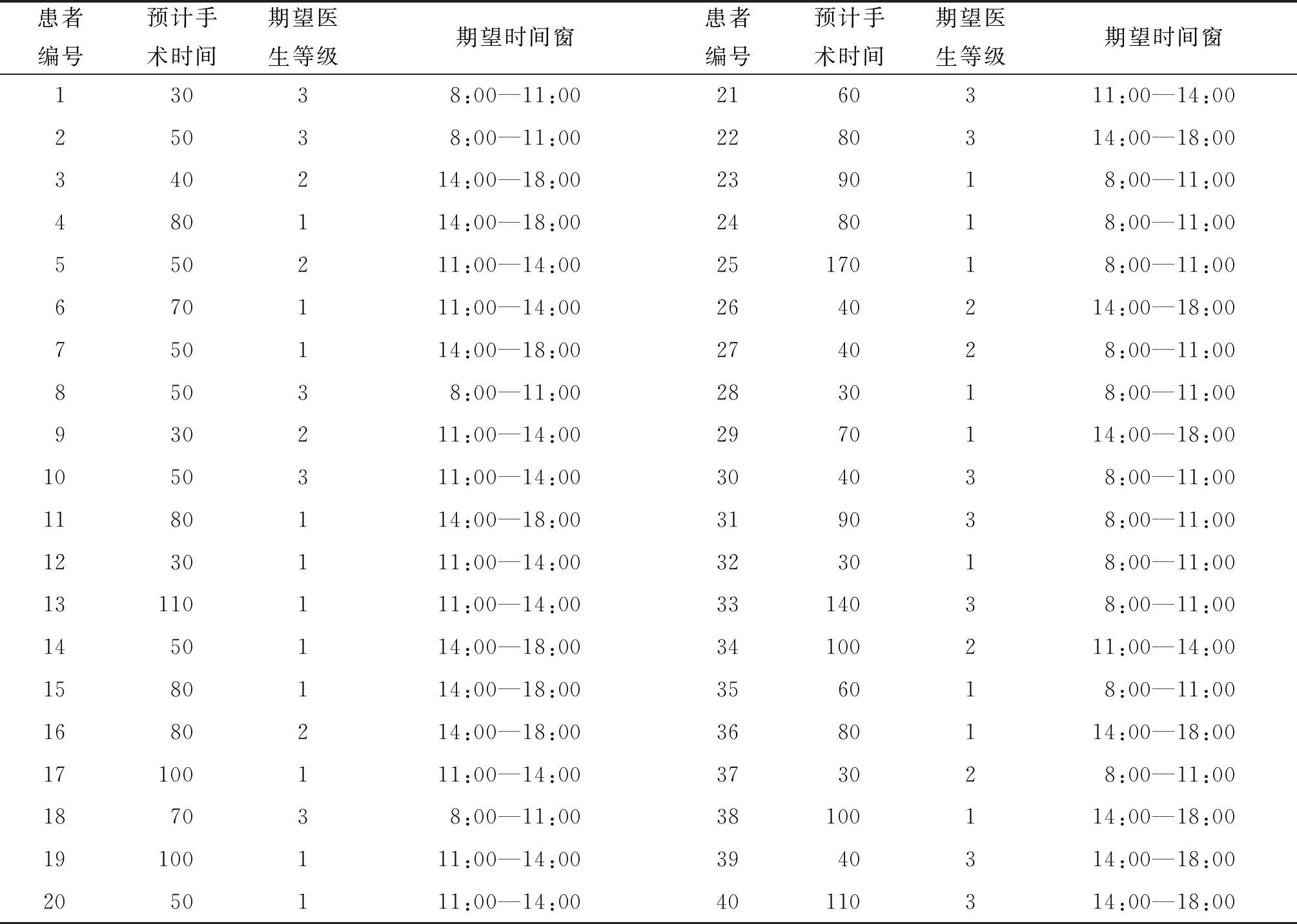
表2 患者手术预计时间、期望医生等级和期望时间窗Table 2 Patient expected time of surgery, expected physician grade, expected time window

每位医生以往对每一类手术的平均治愈率如表3所示。

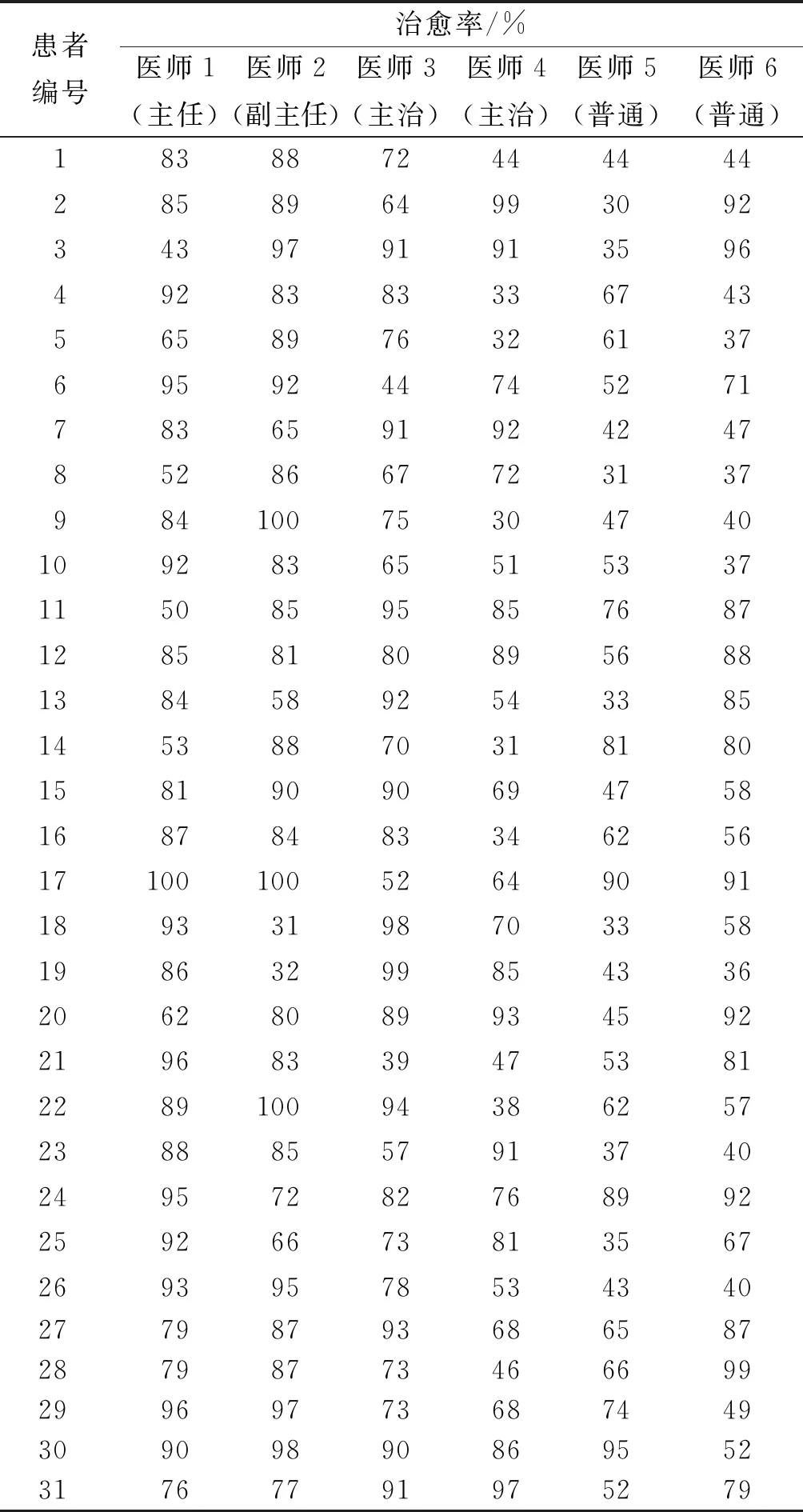
表3 医生-病人疾病的治愈率Table 3 Doctor-patient cure rate

基于以上参数设定，分别根据启发式算法及改进启发式算法流程，采用python编程语言对上述算例进行仿真求解。

所得结果如图9～14所示，图9，10分别为根据启发式算法及改进启发式算法所得到的该工作日各手术室内的排程方案，其中每台手术序号对应长度为该手术在安排给该手术的医生和助理团队配合下所需手术时长。图11，12分别为根据启发式算法及改进启发式算法所得的该工作日内每位医生的手术安排结果。图13，14分别为根据启发式算法及改进启发式算法所得的该工作日内对每个助理团队的手术安排结果，其中数字1～40为患者的序号。

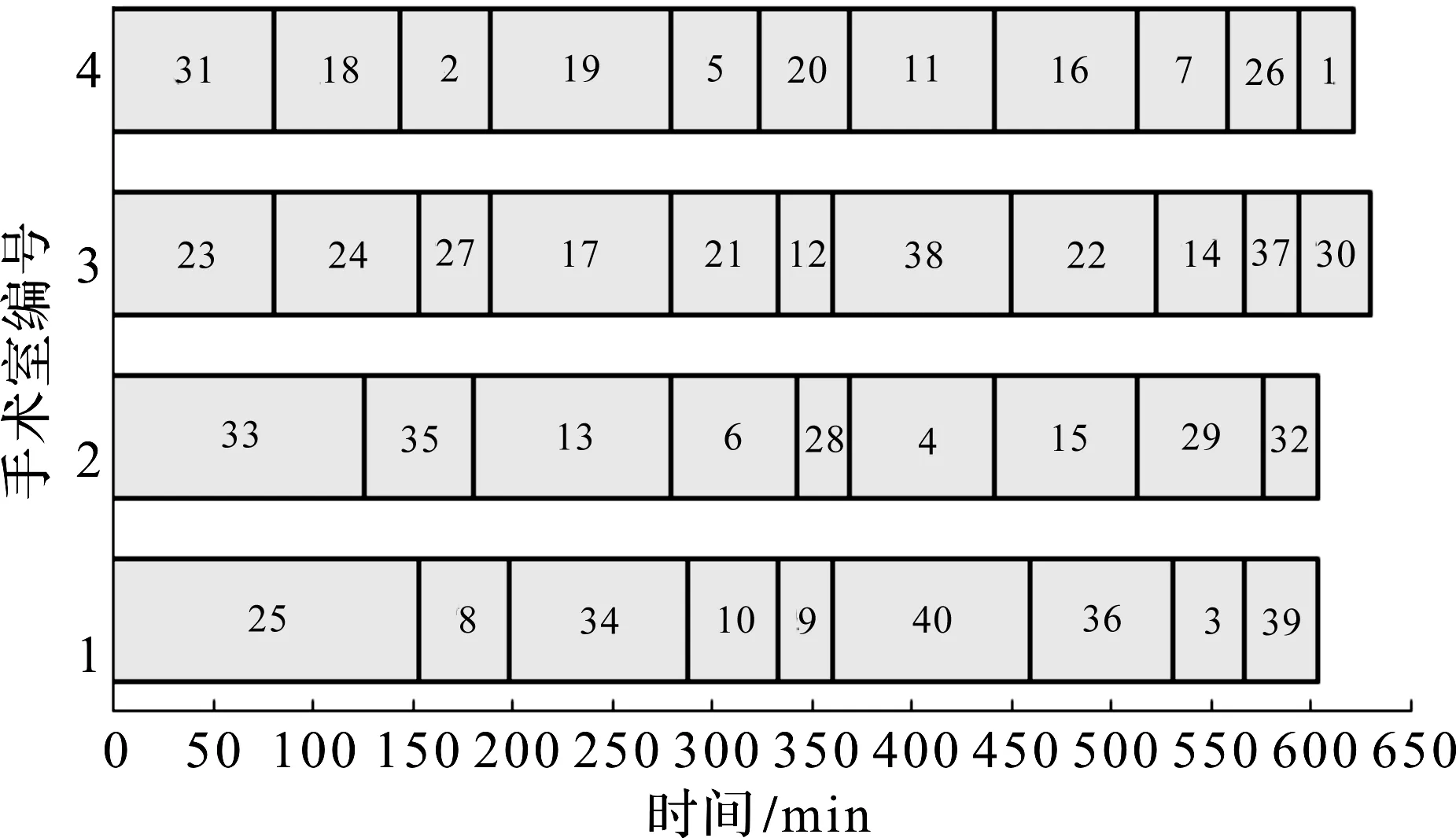
图9 启发式算法手术室排程方案Fig.9 Heuristic algorithm operating room scheduling scheme

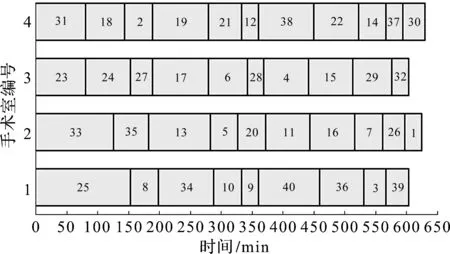
图10 改进启发式算法手术室排程方案Fig.10 Improved heuristic algorithm operating room scheduling scheme

图11 启发式算法医生手术排程方案Fig.11 Heuristic algorithm doctor scheduling scheme

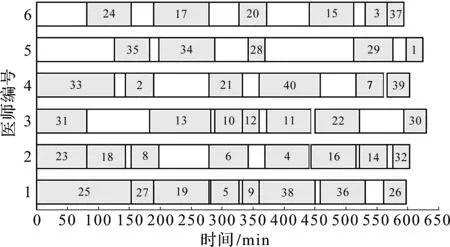
图12 改进启发式算法医生手术排程方案Fig.12 Improved heuristic algorithm for doctor scheduling scheme

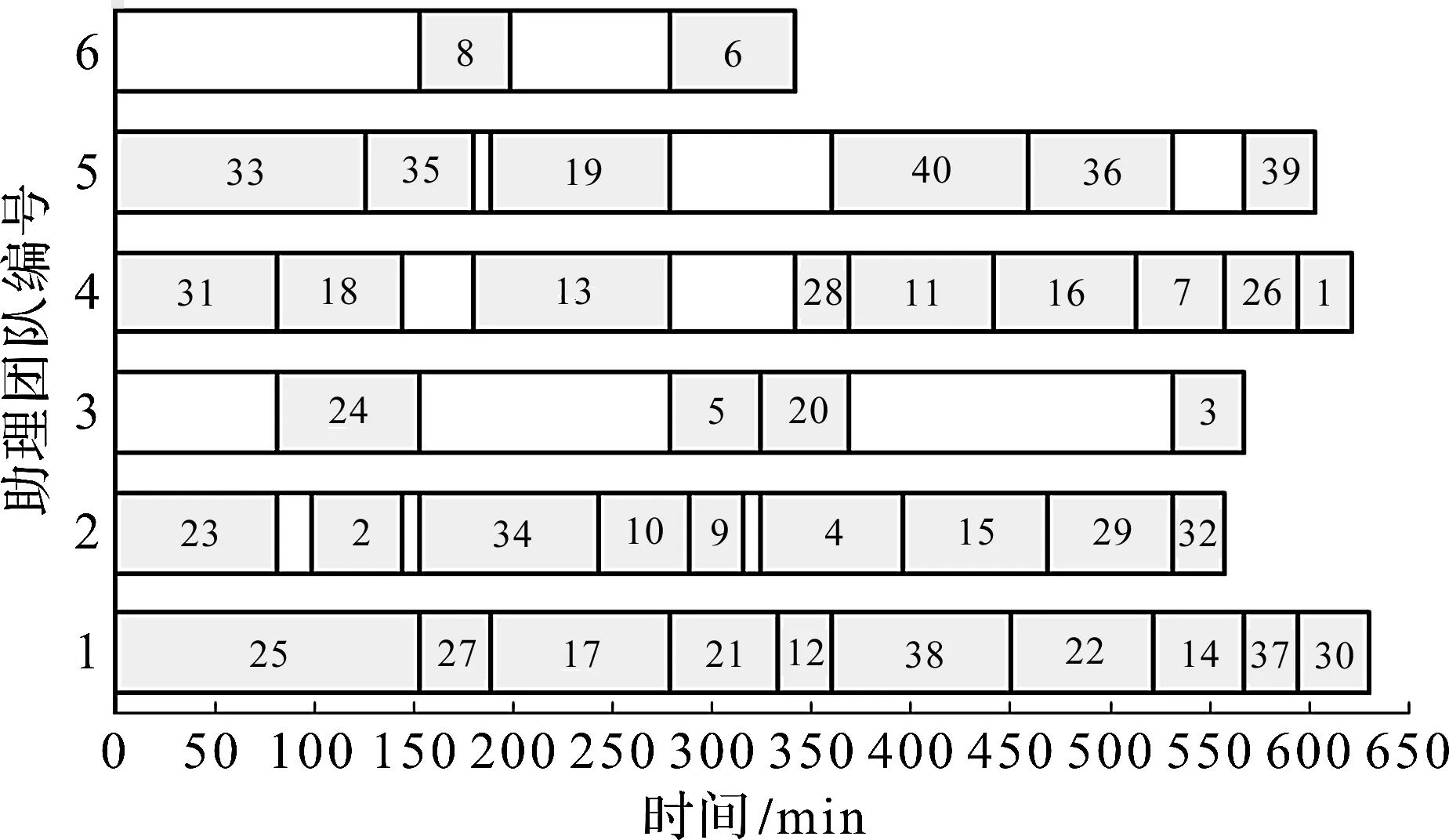
图13 启发式算法助理团队手术排程方案Fig.13 Heuristic algorithm assistant team surgery scheduling scheme

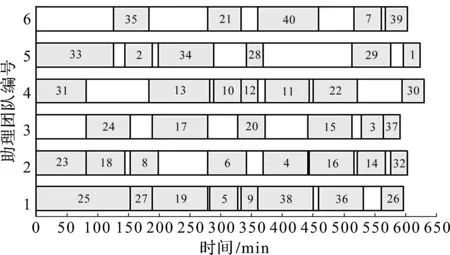
图14 改进启发式算法助理团队手术排程方案Fig.14 Improved heuristic algorithm assistant team surgery scheduling scheme

根据排程结果，启发式算法的4间手术室的加班时长分别为3，3，30，21 min，改进后启发式算法的四间手术室的加班时长分别为3，24，3，30 min。启发式算法的4 个目标函数值分别是：最小化最大手术完成时间630 min，最小化总成本3 477元，最大化满意度为85.23，最大化治愈率为32.78。而改进启发式算法的4 个目标函数值分别为：最小化最大手术完成时间630 min，最小化总成本3 472元，最大化总满意度为87.49，最大化总治愈率为32.11。改进启发式算法在4 项目标函数中最小化最大完成时间与改进前相同，最小化总成本及最大化总满意度均优于原启发式算法，最大化总治愈率略低于原启发式算法。但关于最大化治愈率，考虑到医护人员的疲劳程度同样会影响手术治愈率，所以可认为安排更合理，极大降低医护人员疲劳程度的改进后算法在治愈率一项上也不弱于原启发式算法。

而改进前启发式算法所得该工作日内每位医生的工作时间分别为630，522，198，522，477，108 min，每个助理团队工作时间分别为630，522，198，522，477，108 min。改进后启发式算法所得该工作日内每位医生的工作时间分别为549，468，432，405，264，342 min，每个助理团队工作时间分别为549，468，342，432，378，291 min。

分别计算改进前后各医生和各助理团队工作时间的标准差可得：启发式算法医生和助理团队工作时长标准差均为188.91，188.91 min，改进后启发式算法各医生和各助理团队工作时长标准差分别为90.49，84.63 min，如表4所示。可以看到改进后启发式算法安排出的医生和助理团队的工作时长平均化方面体现出明显优势，即对这两种资源的调度更具人性化和合理化。

表4 两种算法求解算例结果Table 4 Two algorithms solve the results of the examples

5 结 论

研究构建了考虑时间、成本、手术中医患满意度(偏好)的排程问题模型，考虑了受患者对手术时间的期望时间窗和对主刀医生的期望影响的患者满意度、受医生和手术小组的配合熟练度影响的医生满意度，医生过往治愈率代表的医院满意度，通过启发式算法解决手术排程问题。同时考虑到医生及助理小组连续工作安排的合理性，对启发式算法加以改进，从而得到了比原本提出的启发式算法更优的结果。研究尽管对于满意度难以量化的问题提出了一种解决方式，但如何将研究与现实中手术室安排相结合仍需进一步实践调查。后续研究将考虑手术排程问题中的其他相关影响因素，探究更恰当、更加符合实际情况的单目标和多目标数学模型及相关智能优化算法，提出更加完善、合理、高效的手术排程问题方案。