阶跃响应在系统超调抑制中的运用

岳志明

（酒泉职业技术学院 机电工程学院 甘肃省酒泉市 735000）

控制系统的超调抑制，已有多种方法的实践应用：有选择或改进算法来提升超调抑制效果的，如针对具有非线性、强耦合以及高速、高加速度等特性的高速并联机械手臂的末端精确定位和抖动抑制问题，提出改进的自抗扰控制解决方案，并用自适应算法对耦合参数进行实时在线辨识，使关节的超调得以减少[1]；在玻璃窑炉窑压的控制中；结合整体最优滚动优化函数及最优控制增量快速求解方法，从本源出发抑制阶跃跟踪过大的超调，计算量小，并易于实施[2]。马蹄焰窑炉热工系统很难建立有效的机理模型，针对控制计算量大、控制超调问题，采用加权滚动优化函数求解微超调广义预测控制律，增强了算法对被控对象特性跳变的跟踪能力[3]；针对惯导系统超调抑制，提出一种基于小波分析突变信号检测技术的自适应方法，能快速、准确地定位、自适应地有效抑制状态切换产生的超调误差[4]；有分析采用 PI 速度调节器的可控硅直流调述系统产生速度超调的原因，提出了用超调抑制器不影响快速性而实现无超调的措施[5]。还有设计输入轨线来提升超调抑制效果的，如已有的城轨ATO 控制方法由于控制算法过于复杂，或者需要迭代求解且计算时间不确定等，难以在工程上实现，通过改进算法，设计了采用二次曲线的平滑的牵引和制动目标曲线[6]；有对直流电动机起动进行变分，最终采用了抛物转速轨线，提高了起动能效[7]。有对每个阶段的速度滑模函数进行设计，减小了瞬时超调量[8]。有利用闭环阶跃响应所得数据，对于被控对象模型未知的控制系统，进行PID 控制器的比例系数、积分常数以及微分常数整定，使系统的响应性能更优[9]。有研究切换自治线性系统在切换镇定前提下的暂态性能优化，提出基于分路径状态反馈切换的局部暂态优化的设计算法，获得暂态性能估计[10]。

考虑到阶跃响应包含了系统的全部控制特性，故本文反相利用阶跃响应，重新设计输入轨线，并实现了超调抑制性能。即采用阶跃+阶跃响应超调段的反相曲线作为输入，并进而采用了接入时间点提前至速度拐点处接入该反相曲线，取得了超调抑制的实效。

1 二阶系统阶跃响应超调的时域分析

对于典型二阶系统

考虑到阶跃响应曲线的起动时段的速度拐点，取阶跃曲线二阶导数为零，有：

即得在拐点处的相位为

故而轨点tg与上升时间点tr的相位提前量为

2 设计超调抑制的输入曲线

（1）取输入信号为：阶跃+在上升时间点tr加入反相的阶跃响应超调段曲线

此时的输入曲线为：

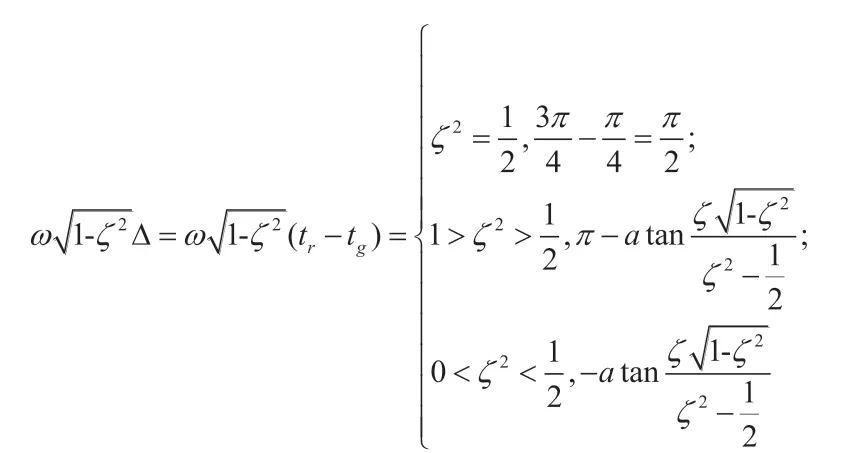
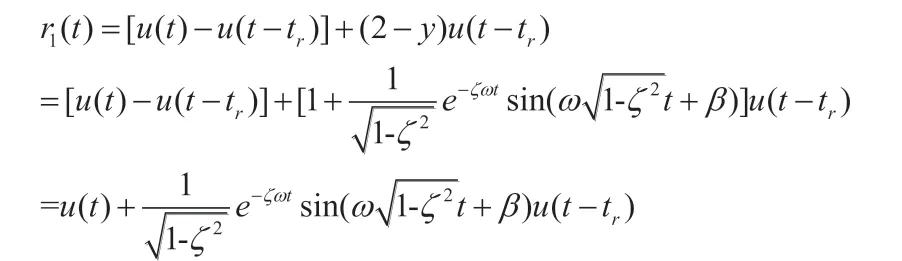
通过卷积求得此时的响应

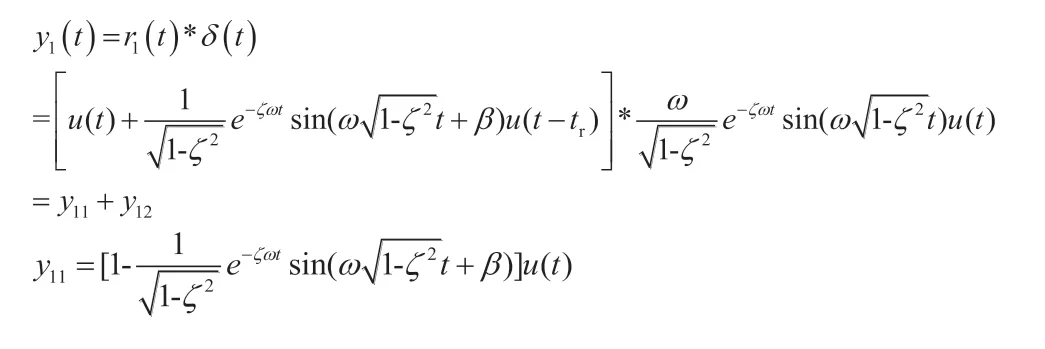
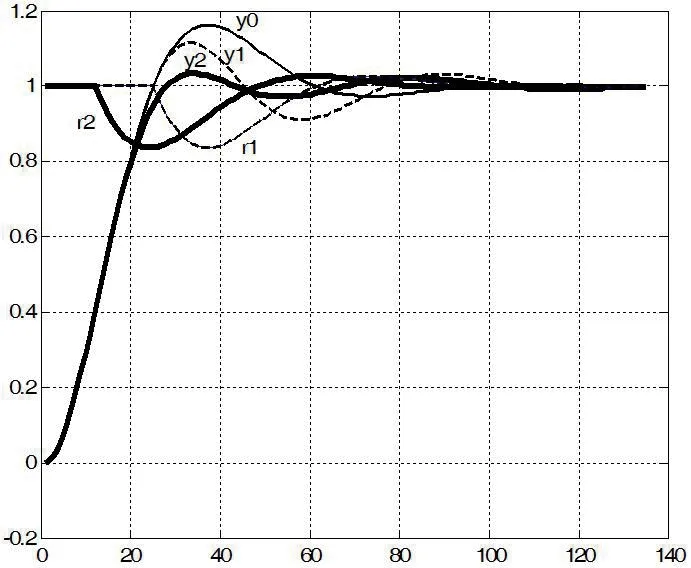
图1

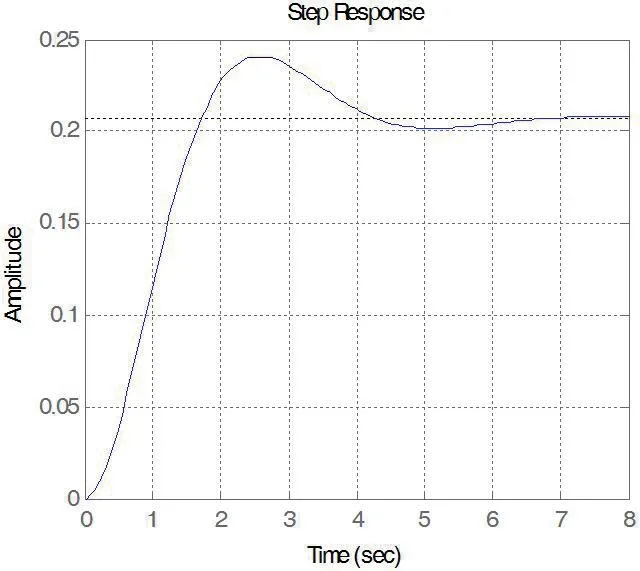
图2

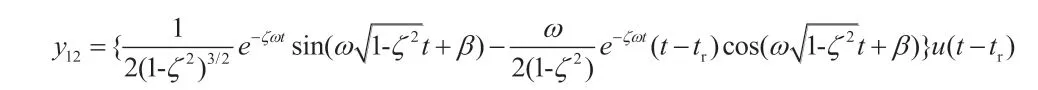
y12为“超调抑制分量”。

取ζ=0.5，ω=1 得仿真曲线如图中r1、y1所示，其中y0为阶跃响应曲线，可见取得了超调抑制的效果。

（2）反相接入时间点提前的方法，即取输入信号为：阶跃+在拐点tg加入反相的阶跃响应超调段曲线

为进一步减小超调、同时保证快速性能不降低太多，将反相抑制加入点，由tr提前到阶跃曲线起动时段的速度拐点tg处，此时的输入为r2(t)：

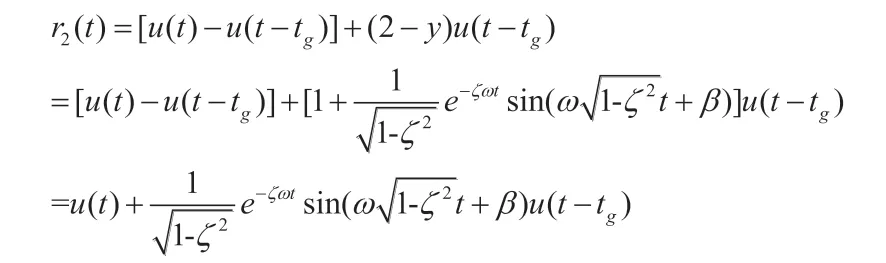
由卷积求输出响应，有

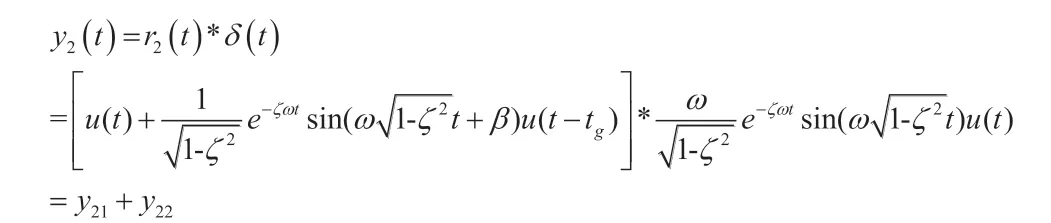
其中

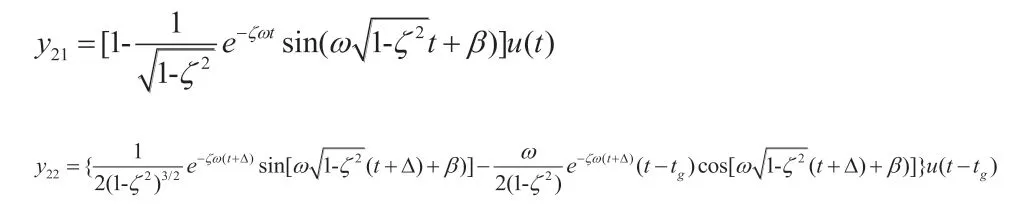
y22为“超调抑制分量”。

此时，取 ζ=0.5，ω=1 时得仿真曲线如图1 中r2(t)、 y2(t)、所示。可见调节时间没有损失，同时取得了超调抑制更好的效果，峰值依次由 yp0=1.1630、yp2=1.1326 降为 yp2=1.0401，即超调由16.30%降为4.01%。

（3）比较二次型最优控制超调性能

取Q=diag([1,1])，R=1，N=[0,1]’，得到闭环系统阶跃响应曲线如图2所示，其超调量为16.4%。

3 结语

（1）采用二阶系统阶跃响应超调的时域离线方法，设计了超调抑制性能的输入轨线，仿真显示具有较好的超调抑制的作用。

（2）为进一步减小超调，将 r1(t)的加入点确定为速度拐点，从而取得了超调抑制更好的效果，同时保证了调节时间没有损失。

（3）该离线的超调时域抑制方法，避免了实际系统控制所必需的建模、进行算法设计以及实时运算量大等困难，具有应用简单、易于实施的特点。易于与反馈等控制方法结合而达到更优的应用方案。