关于二维线性自治系统的相图的教学
樊自安
(湖北工程学院 数学与统计学院,湖北 孝感 432000 )
解的稳定性理论是“常微分方程”课程中的一个重要知识点,如何正确作出二维线性自治系统的相图是一个教学重点。在几本经典的教材中[1-5],仅给出了相图的大致思路,但要作出二维线性自治系统的相图,特别是奇点是两向结点的二维线性自治系统的相图,学生一般感觉较困难。文献[6]以极坐标为基础,借助仿射变换,研究了二维线性自治系统的相图;文献[7]对平面齐次多项式系统的平衡点的稳定性进行了分析,并给出对应系统的全局相图及具体系统,关于微分系统的稳定性,参考文献[8-10]。
对于二维线性自治系统:
(1)

系数矩阵A的特征方程为:
(2)
特征根为:
(3)
显然,λ1≥λ2。
考虑二维线性自治系统(1),对于初等奇点(0,0),当λ1和λ2为相等实数时,奇点为单向结点或星形结点;当λ1和λ2为复数时,轨线为向内或向外盘旋的螺线;当λ1和λ2为异号实数时,轨线以y=k1x和y=k2x为渐进线。这些都比较容易作出相图;但当奇点是两向结点时,画相图是教学中的一个难点,本文仅讨论λ1和λ2为同号不等实数即奇点是两向结点的相图。
1 主要结果及证明
当λ1和λ2为同号不等实数时, (a-d1)2+4bc>0,λ1≠λ2,由式(3)λ1>λ2,这时奇点是两向结点。分三种情见讨论。
1)b(λ-a)≠0,设矩阵A的特征值λ1和λ2对应的特征向量分别设为ξ1,ξ2,取
(4)
方程组(1)的通解为:
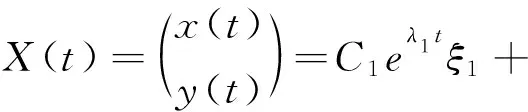
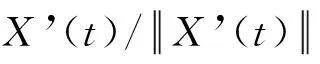
即当t→+∞,轨线X(t)的切线趋于平行于向量ξ1,当t→-∞,轨线X(t)的切线趋于平行于向量ξ2。
下面我们将证明向量ξ1、ξ2的斜率为k1,k2,其中k1,k2这样解出:
即:
bk2+(a-d1)k-c=0
(5)
(6)
由式(3)和式(4)得向量ξ1的斜率:
=k1,
向量ξ2的斜率:
=k2,
轨线X(t)逐渐趋向于(0,0)或远离(0,0),直线y=k1x,y=k2x都经过原点(0,0),因此t→+∞,轨线X(t)的切线趋于y=k1x,当t→-∞,轨线X(t)的切线趋于y=k2x。
2)b=0,由式(3)知λ1=a,λ2=d1,不妨设a>d1,λ1>λ2。
设矩阵A的特征值λ1和λ2对应的特征向量分别设为ξ1,ξ2,则由(A-λE)x=0,可取
(7)
由于λ1>λ2,由第一种情况的讨论可知,当t→+∞,轨线X(t)的切线趋于平行于向量ξ1,
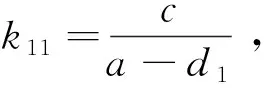
3)λ=a,由式(2)知bc=0,这时b≠0,c=0;若b=0第二种情况已讨论。由式(3)知λ1=a,λ2=d1,不妨设a>d1,λ1>λ2。
设矩阵A的特征值λ1和λ2对应的特征向量分别设为ξ1,ξ2,则由(A-λE)x=0,可取
(8)
由于λ1>λ2,由第一种情况的讨论知当t→+∞,轨线X(t)的切线趋于平行于向量ξ1,
当t→-∞时,轨线X(t)的切线趋于平行于向量ξ2,由式(8)得ξ1的斜率k11=0,向量ξ2的斜率:k12=(d1-a)/b,而由式(6)解出k1=0,k2=(d1-a)/b,则k11=k1,k12=k2仍然成立,因此式(6)仍成立。
因此我们得到下面的定理:
定理1 当二维线性自治系统(1)的系数矩阵A的特征根λ1,λ2为同号不等实数时,系统(1)的轨线与直线y=k1x,y=k2x的其中一条切于原点(0,0),其中k1,k2由式(6)给出(当只解出一条直线斜率k1时,另一条直线为x=0)。
轨线究竟与哪一条直线相切呢?
由式(6)知,k1>k2,t→+∞,轨线X(t)的切线趋于y=k1x,这说明,当t→+∞,轨线X(t)的切线的斜率在逐渐增大,在y=k1x与y=k2x之间,轨线上的点的二阶导数大于0,这说明在y=k1x与y=k2x之间,轨线是向下凹的。根据这个性质,我们画出第一或第二象限内系统的相图(这里没有画箭头的方向,箭头的方向不影响相图的上述性质),如图1和图2所示。
从图1和图2可以看出,在y=k1x与y=k2x之间,在第一象限内, 轨线X(t)与y=k2x相切或在第二象限内,轨线X(t)与y=k1x相切。因此我们得到下面的定理:
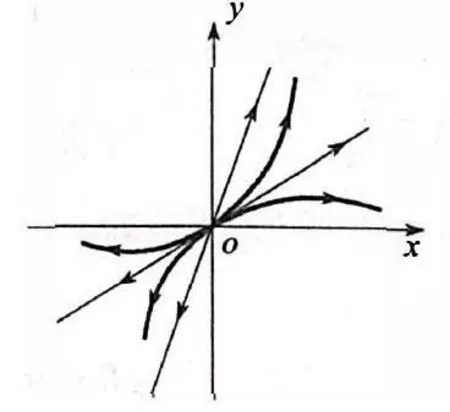
图1 k1>k2>0
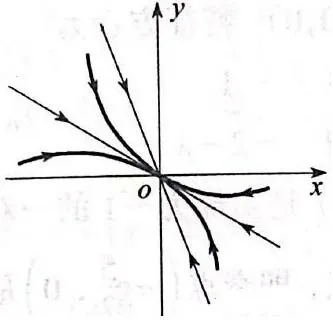
图2 k2 图3 k1=3,k2=1 定理2 当二维线性自治系统(1)的系数矩阵A的特征根λ1,λ2为同号不等实数时,在y=k1x与y=k2x之间,在第一象限内,系统(1)的轨线与y=k2x相切或在第二象限内,系统的轨线与y=k1x相切。其中k1>k2,k1,k2由式(6)给出(当只解出一条直线斜率k1时,另一条直线为x=0)。 例确定系统 的奇点类型,并作出相图。 解(0,0)是唯一奇点,特征方程λ2+4λ+3=0,特征根λ1=-1,λ2=-3是同号相异实根,奇点(0,0)是稳定结点。由 解出k1=3,k2=1,k1>k2,两条渐进线方程y=3x,y=x,由定理2,在第一象限内,系统的轨线与y=x相切,如图3所示。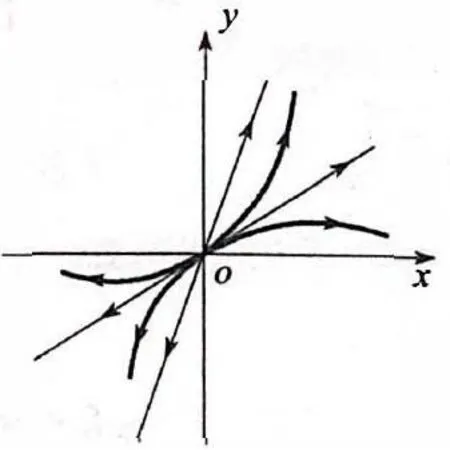
2 例子说明

