市域高架铁路不同轨道结构的特征频率及弹性不平顺对比研究

杜运国，苟长飞，史 吏，陈致远，姜建伟

(1.温州市铁路与轨道交通投资集团有限公司，浙江 温州 325000；2.浙江工业大学 土木工程学院，浙江 杭州 310023)

轨道交通是当前缓解城市交通拥堵、提升生活出行品质的首选交通方式[1]。为节约土地资源，城市轨道交通多采用地下或高架形式。在深厚淤泥质软土地区，例如温州[2]，地铁施工面临掌子面稳定性和沉降变形控制性较差等问题[3]，因而更倾向于采用高架线路。城市高架轨道交通线路多采用无砟普通道床结构，在有减振要求的地段，则采用减振道床。相较于普通道床将轨道板与高架桥桥面直接浇筑为一体，减振道床则在轨道板和桥面之间增设橡胶垫或钢弹簧，使得轨道板“浮”于桥面上，进而利用浮置板的屏蔽效应来滤去高于其特征频率、向下传播的振动分量[4]。现有研究多采用叠合梁模型[5-8]或三维实体有限元建模[9-10]来分析上述各种轨道结构的动力响应和特征频率，但研究多限于普通路基或地铁线路，针对城市高架线路无砟普通道床和减振道床的特征频率的研究相对较少。竖向轮轨作用力的来源主要是由于轨道的高低不平顺，而轨道不平顺主要有与荷载无关的几何不平顺和比例于荷载的弹性不平顺两种类型[11]。其中，几何不平顺是由钢轨波形磨耗、钢轨初始弯曲、道床松动和局部差异沉降等因素引起的，现有研究中多将其考虑为随机过程[12-14]。钢轨等轨道构件均为弹性体，同时考虑到扣件、枕木和轨道板的非连续支承，使得原本几何平顺的轨道在列车轮对下也会出现沿轨道延伸方向的高低不平顺，即为弹性不平顺[15]。显然，相较于几何不平顺的随机性，弹性不平顺取决于轨道结构以及列车轮对的具体物理力学性质，是一种确定性输入。现有轨道不平顺测试中的直接法(如惯性基准法和弦测法[16])是针对轨道的几何不平顺，但近年来发展起来的通过运营列车的轮轨振动加速度[17]或轮轨噪声[18]换算轨道不平顺的间接测试法，在严格意义上测试的是几何和弹性不平顺的叠加。现有研究多未对几何不平顺和弹性不平顺作严格区分，也未见针对不同轨道结构形式弹性不平顺的研究报道。笔者针对无砟普通道床、橡胶垫减振道床和钢弹簧浮置板道床等3 种城市高架轨道结构型式，建立了3层叠合梁轨道结构模型，并引入Hertz线性接触实现了列车轮对和叠合梁轨道结构的动力耦合，对比分析3 种轨道结构的特征频率，并特别提供了3 种轨道结构对应于不同波长的弹性高低不平顺幅值，研究结果可为城市高架线路轨道结构比选以及轨道不平顺管理提供依据。

1 工程背景

我国某沿海城市的市域铁路全线采用高架形式，原设计采用双块式无砟普通道床。但由于线路近距离经过某振动敏感构筑物(最小间距仅为9 m)，为降低列车运行的环境振动影响，该线路段拟采用减振道床结构。原设计的双块式无砟普通道床和拟采用的橡胶垫减振道床及钢弹簧浮置板道床的构造细节，分述如下。

1) 双块式无砟普通道床结构如图1所示，包括钢轨、扣件、双块式轨枕和道床板等部分。其中，钢轨采用60 kg/m、无螺栓孔U75V新轨，焊接无缝线路；扣件采用WJ-7B型扣件，扣件间距一般为600 mm；轨枕采用SK-1型双块式轨枕，轨枕与道床板浇筑为一个整体；道床板分块浇筑于桥面上，道床板宽度为2 800 mm，长度一般为5～7 m。

2) 橡胶垫减振道床结构如图2 所示，包括钢轨、扣件、双块式轨枕、道床板、限位凸台、橡胶减振垫和底座砂浆找平层等部分。其中，钢轨、扣件、轨枕和道床板与上述普通道床基本相同，但轨道板和桥面之间采用橡胶减振垫，减振垫厚度为27 mm，静刚度为0.025 N/mm3。

图2 橡胶垫减振道床结构示意图Fig.2 Schematic diagram of rubber cushion vibration track bed

3) 钢弹簧浮置板道床结构如图3所示，包括钢轨、扣件、双块式轨枕、浮置板和弹簧隔振器等部分。其中，钢轨采用60 kg/m的无缝钢轨；扣件采用DTV I-2型扣件，扣件间距一般为625 mm；轨枕采用SK-1型双块式轨枕，轨枕与浮置板浇筑为一个整体；浮置板采用C40混凝土分块浇筑，浮置板宽度为3 510 mm、厚度为293 mm，长度为7 m；弹簧隔振器动刚度为6.9 MN/m，弹簧纵向中心间距为1.25 m。

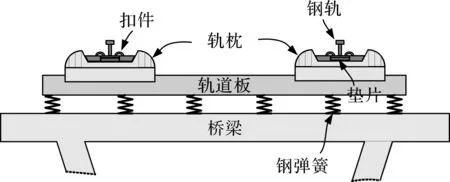
图3 钢弹簧浮置板道床结构示意图Fig.3 Schematic diagram of steel spring floating slab track bed

2 计算模型

上述3 种轨道结构均包括了钢轨、轨道板和桥梁，在竖向动力响应分析中，可将三者考虑为3层叠合梁，扣件、板下橡胶垫/钢弹簧和桥梁支座则模拟为叠合梁之间的离散弹簧和阻尼器。在此基础上，通过引入轮轨Hertz线性接触，可实现列车轮—轨道结构—桥梁的竖向动力耦合分析。

2.1 移动荷载—轨道—简支箱梁竖向动力分析模型

等跨简支箱梁的长度为L，上方覆盖有沿纵向等长但间断的轨道板，板上钢轨采用扣件固定，移动谐振荷载施加在钢轨上，有限长且两端自由的Euler梁可替换箱梁和轨道板，而钢轨则简化为无限长的Euler梁，用离散支承的复刚度弹簧来模拟钢轨扣件、板下橡胶垫/钢弹簧和箱梁底部的支座，其结构如图4所示。由图4可知：3层叠合梁单元是由长度为L范围内的箱梁、轨道板梁和钢轨梁组成，当该梁单元沿纵向无限重复延伸时(不计跨间箱梁间距)，即可形成周期为L的周期结构。

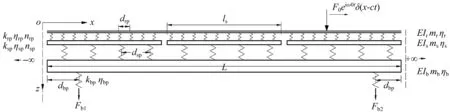
图4 移动荷载—轨道—简支箱梁竖向动力分析模型Fig.4 Analysis model on vertical interactions between moving load, track and simply supported girder

其中梁的抗弯刚度为EI、线质量为m、频域滞回阻尼比为η，分析模型中的钢轨、轨道板和箱梁分别用下标“r”“s”“b”表示；在箱梁长度L范围内有ns个长度为ls的轨道板，且不计相邻轨道板间距；弹簧刚度记为k、支承间距为d、频域滞回阻尼比为η，钢轨扣件、板下垫层(橡胶垫或钢弹簧)和橡胶支座在分析模型中用下标“rp”“sp”“bp”表示，应注意dbp表示橡胶支座距箱梁端截面的最近间距(方向沿纵向)；nrp和nsp分别表示每块轨道板上部和下部的离散弹簧数目。在每跨箱梁底部沿纵向方向均设有两个橡胶支座。轨道结构各几何和材料参数符号详见图1，且各几何参数需满足L=nsls和ls=nrpdrp=nspdsp。

(1)

(2)

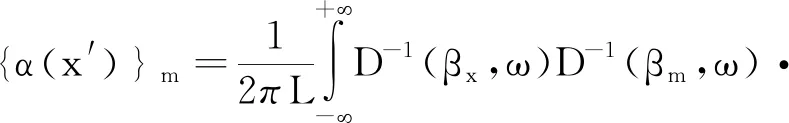
(3)

(4)

式中：I为nsnrp×nsnrp的单位阵；χ(·)为nsnrp×1的矢量，Λ(·)为nsnrp×nsnrp的方阵，二者的元素可表示为

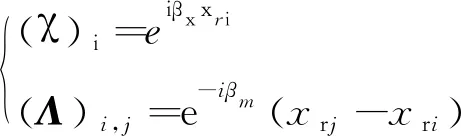
(5)

式中：xri为第0个叠合梁单元中第i个扣件弹簧的坐标；x′=x-x0-ct为随荷载一起移动的坐标轴；βx为波数；ω0为荷载自振频率；c为荷载速度；x0为点荷载初始位置(t=0)；而式中的D(βx,ω)，ω，βm三者的元素又可以表示为

(6)

模型中各弹簧反力的时域响应可同样采用关于波数βx的Fourier逆变换得到，此处以第0个叠合梁单元中的扣件弹簧反力矢量Fr0(t)为例，可表示为

(7)

2.2 轮轨动力相互作用模型

在图4所示轨道和简支箱梁模型的基础上，添加列车车轮，建立起轮轨动力相互作用模型，如图5所示。图5中W表示车辆的轴荷载；kH表示轮轨Hertz接触弹簧刚度；mw表示轮对质量。

图5 轮对—轨道—桥梁动力相互作用分析模型Fig.5 Analysis model on dynamic interactions between wheel, track and bridge

移动列车轮对和周期叠合梁间的动力相互作用可以参考文献[19]的Fourier级数展开法来求解，列车轮对考虑为刚体，其竖向位移为uw，可有竖向振动控制方程式为

(8)

式中P(t)为轮轨作用力。由于轨道是关于箱梁跨长L的周期结构，则P(t)应为L/c的周期函数，可表示为

(9)

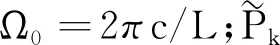
(10)

式中gk为轮对在kΩ0频率分量的动柔度。根据式(8)，gk可表示为

(11)

由式(1)可得移动坐标系x′中轮轨接触点的钢轨位移方程式为

(12)

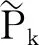
(13)

假设轮对和钢轨之间满足Hertz线性接触关系，则轮对与钢轨之间满足如下位移协调方程式为

uw(t)+ur(t)+δ0+(P(t)-W)/kH=0

(14)

式中δ0为轮对轴载W下的轮轨接触弹簧变形量。将式(12)代入式(14)，可得到轮轨作用力控制方程式为

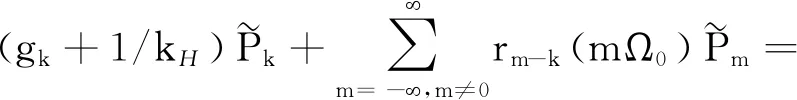
(15)

(16)

2.3 轨道弹性高低不平顺

由于在轮轨位移协调方程(14)中并未引入钢轨的几何不平顺，因此轮轨作用力控制方程(15)的右端项仅包括由轮对轴重与钢轨动柔度相乘确定的挠度输入，同时由式(1)可知：钢轨柔度r-k(0Ω0)取决于具体的轨道结构形式以及轮对移动速度。因而，式(15)的右端项可理解为轨道结构比例于轮对轴重的弹性不平顺[19]，类似于式(9)进行Fourier级数展开，则有弹性不平顺的第k阶谐波(对应波长为λk=L/k)分量可表示为

(17)

式中β0=2π/L。将上式所有的谐波分量进行叠加，即有任意坐标x处的弹性不平顺可表示为

(18)

3 模型验证

采用Fortran语言，可在Intel Visual Fortran平台中对上述公式进行编程实现。Sheng等[15]在针对移动轮对与有砟轨道的动力相互作用的问题时采取了Fourier级数法进行研究，轨道由无限长的钢轨梁、等间距的刚性轨枕质量块以及离散支承的钢轨垫圈弹簧和道砟层弹簧构成。道砟层弹簧的底部固定，从而考虑刚性地基。将3层叠合梁模型(图4)中箱梁以及轨道板的抗弯刚度取大值、将箱梁支座刚度取大值，同时减小轨道板的长度和质量以模拟轨枕质量块，从而实现Sheng等[15]模型中的刚性枕木以及刚性地基。车轮、钢轨、轨枕和垫圈/道砟层弹簧参数均取自Sheng等[15]的论文(表1)，图6对比了退化后3层叠合梁模型以及Sheng等[15]模型给出的轮轨作用力频谱和时程曲线。经过对比发现二者吻合性较好，说明笔者建立的3层叠合梁模型的正确性。

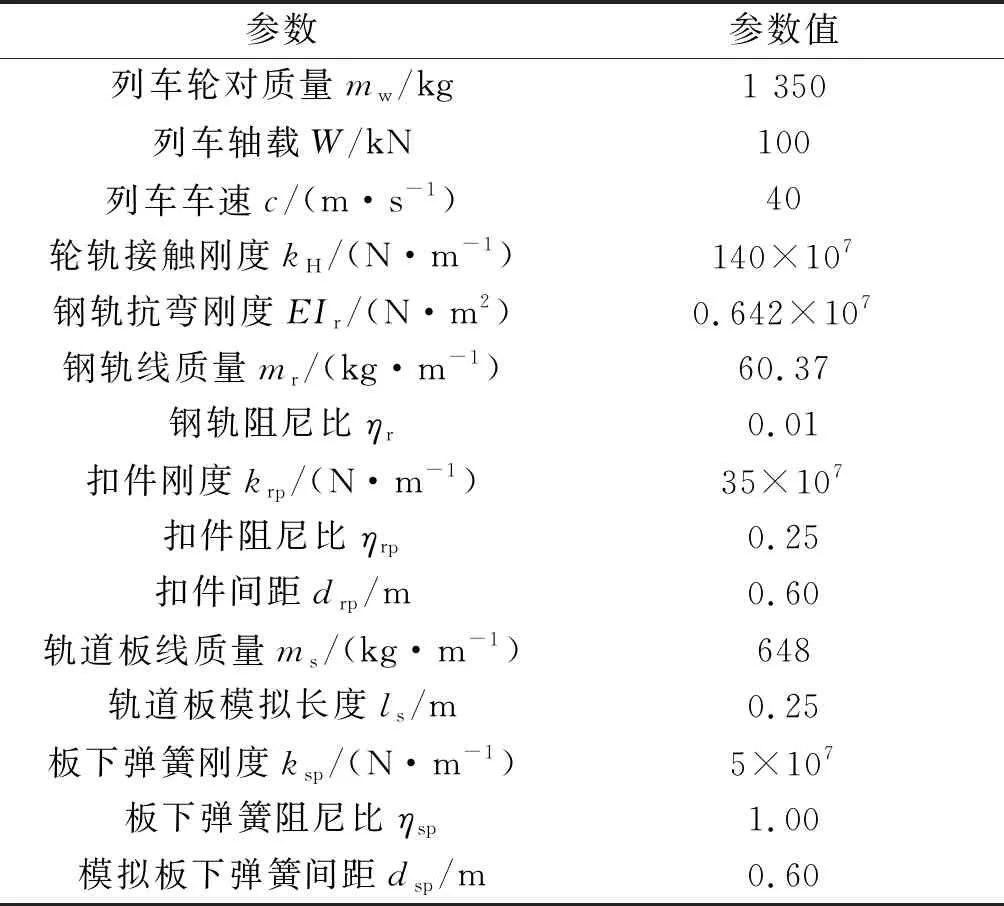
表1 移动列车轮对和有砟轨道模型参数

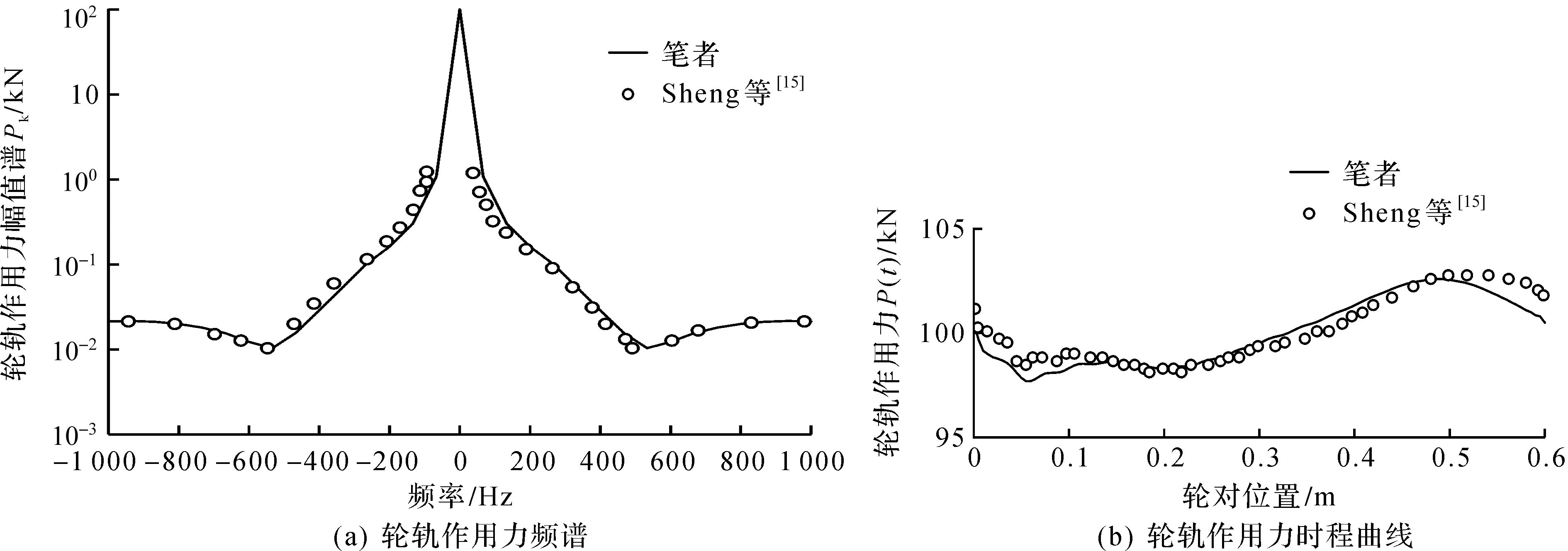
图6 三层叠合梁模型验证Fig.6 Three layer beam model validation

4 模型计算参数

由设计文件可知：列车轮对(考虑单轮对)、橡胶垫减振道床、钢弹簧浮置板道床以及简支箱梁的相关模型参数，如表2～5所示。由于双块式无砟普通道床与橡胶垫减振道床的区别仅在于橡胶垫层，即前者可由后者退化而来。为避免重复，此处不再单独列表给出双块式无砟普通道床的计算参数。

表2 列车轮对模型参数Table 2 Model parameters of train wheelset

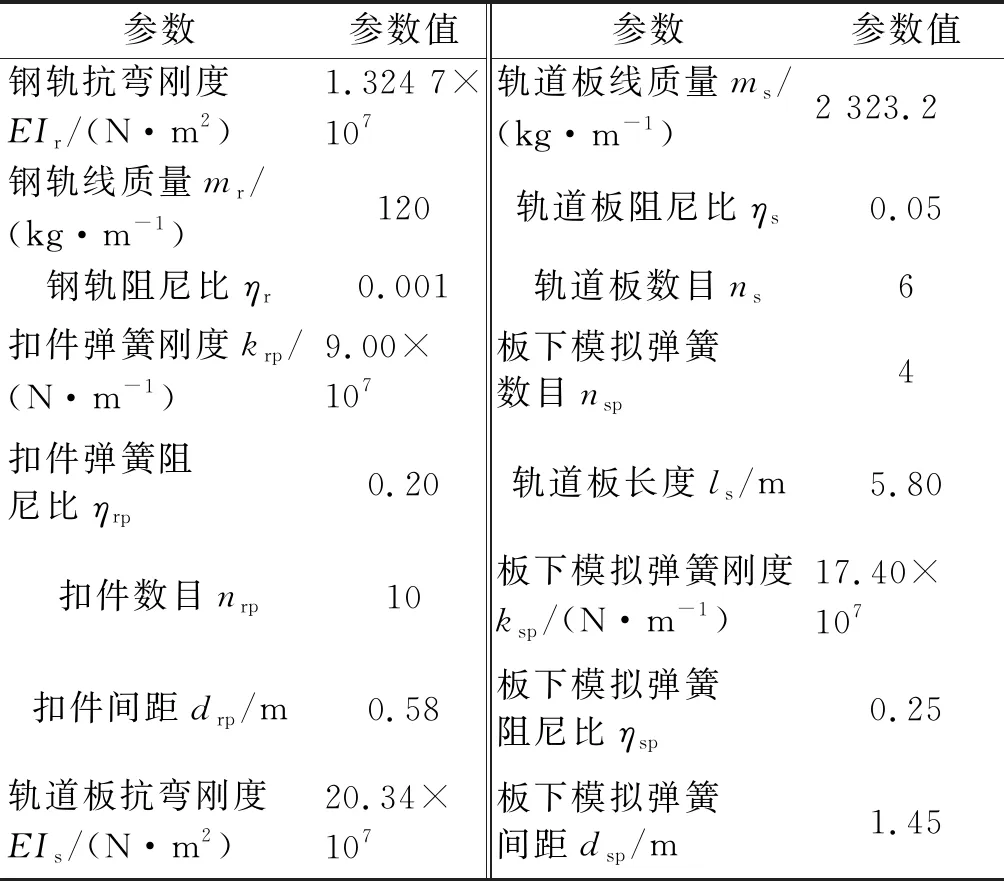
表3 橡胶减振道床计算参数Table 3 Parameters of rubber-pad floating slab track

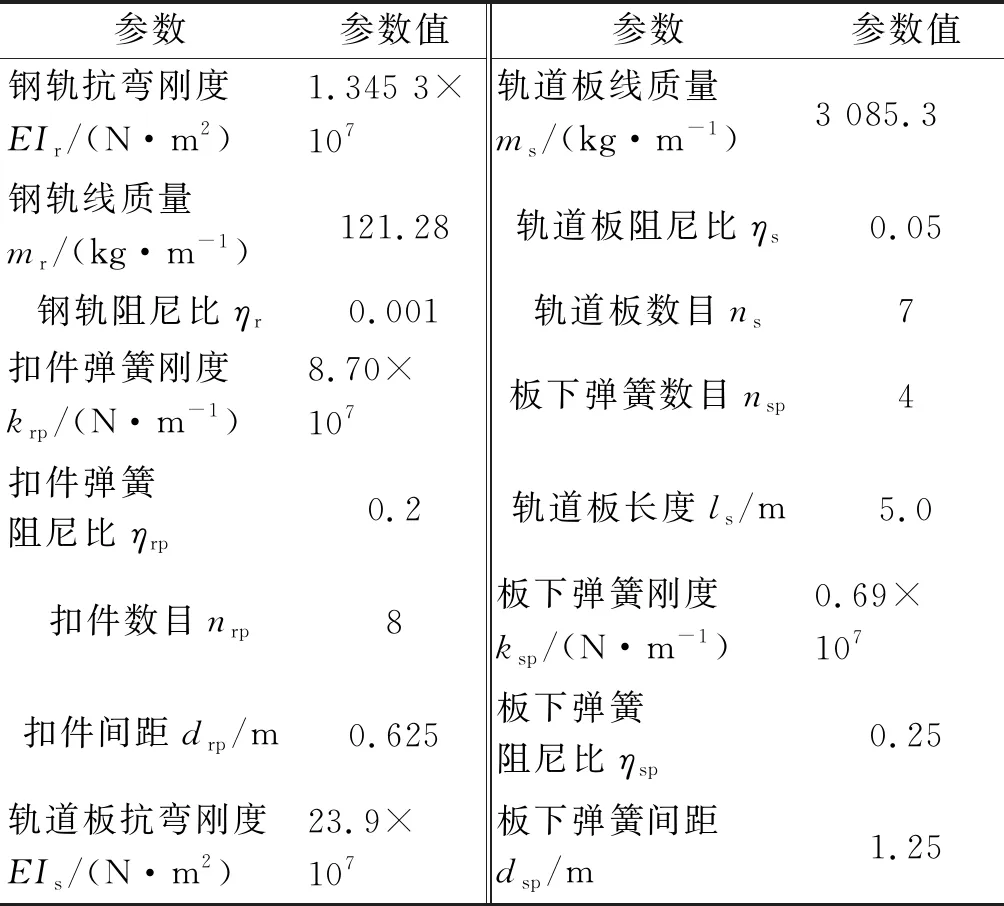
表4 钢弹簧浮置板道床计算参数Table 4 Parameters of steel-spring floating slab track

表5 简支箱梁模型参数Table 5 Model parameters of simply supported box girder

5 模型计算结果及分析

5.1 轨道特征频率

为确定上述双块式无砟普通道床、橡胶垫减振道床以及钢弹簧浮置板道床的特征频率，可在梁跨中点(x0=L/2)和四分之一(x0=L/4)位置处作用静止(c=0)谐振点荷载至钢轨，通过连续改变荷载的自振频率ω0来计算箱梁的支座反力Fb1，确定轨道结构的特征频率。考虑到箱梁支座反力是高架桥下部结构(如桥墩、群桩基础)和地基环境振动的输入源，因而箱梁支座反力是反应不同轨道结构特征频率及减载率的合理指标。

5.1.1 橡胶垫减振道床

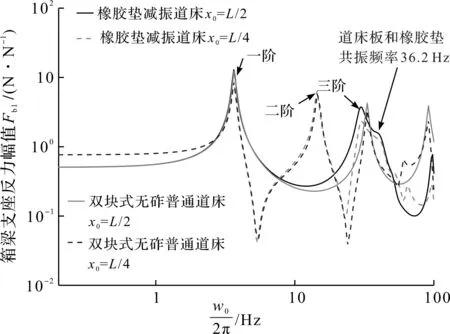
图7 橡胶垫减振道床箱梁左支座反力幅值(与普通道床结构对比)Fig.7 Amplitude of reaction force at left support of box girder carrying the rubber-pad floating slab track (compared with the double-block ballastless track)

5.1.2 钢弹簧浮置板道床

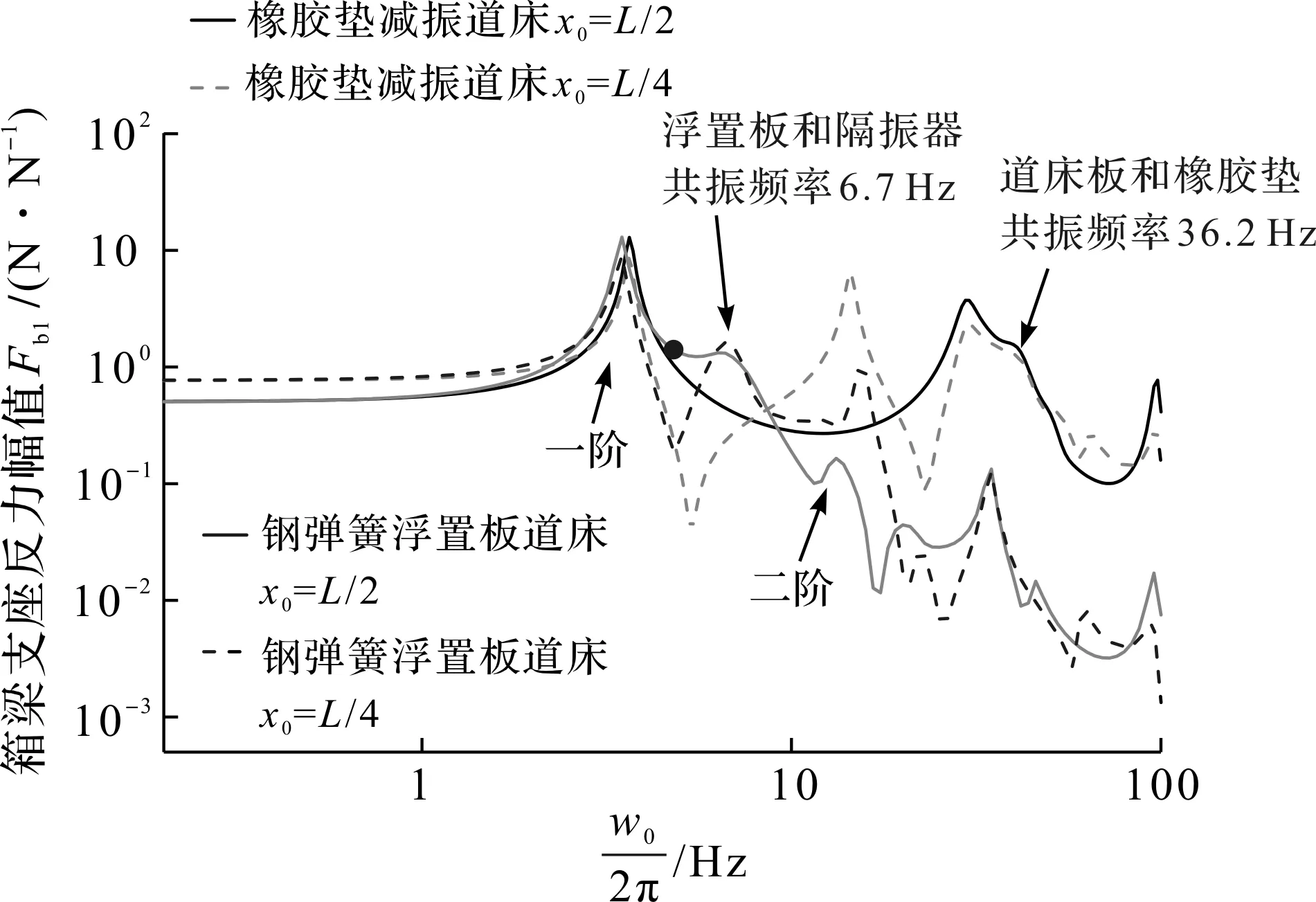
图8 钢弹簧浮置板轨道箱梁支座反力幅值(与轻型橡胶减振道床轨道对比)Fig.8 Amplitude of reaction force at left support of box girder carrying the steel-spring floating slab track (compared with the rubber-pad floating slab track)

5.2 轨道弹性高低不平顺

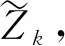
图9 轮对速度20 m/s时轨道弹性不平顺谱Fig.9 Elastic irregularity of track subjected to wheelset moving at 20 m/s

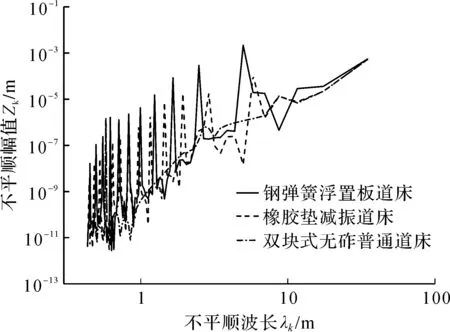
图10 列车行驶速度为40 m/s时不平顺度对比谱Fig.10 Elastic irregularity of track subjected to wheelset moving at 40 m/s

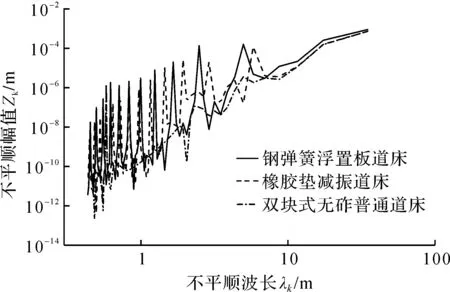
图11 列车行驶速度为80 m/s时不平顺度对比谱Fig.11 Elastic irregularity of track subjected to wheelset moving at 80 m/s

5.3 不同轨道结构的减振效果讨论

城市轨道交通引起的沿线环境振动污染以低频振动分量(频率≤50 Hz)为主。由图7，8可知:橡胶垫减振道床和钢弹簧浮置板道床的特征频率分别为36.2 ，6.7 Hz，二者均能有效滤去频率高于36.2 Hz的振动分量。但对于6.7～36.2 Hz范围内的环境振动分量而言，则钢弹簧浮置板道床的隔离效果更优。但应指出，钢弹簧浮置板道床的低特征频率特性是由高质量轨道板结合低刚度钢弹簧获得的，因而钢弹簧浮置板道床的弹性不平顺最高，这会导致轮轨作用力以及钢轨位移的明显增大。文献[19]规定“浮置板轨道在列车额定荷载作用下的钢轨的最大垂向位移不应大于4 mm”，因而在实际应用时需校核钢弹簧浮置板轨道的钢轨位移是否满足该限值要求。

6 结 论

笔者利用3 层叠合梁模型对比分析了双块式无砟普通道床、橡胶垫减振道床以及钢弹簧浮置板道床等3 种市域高架轨道结构的特征频率以及移动单轮对引起的轨道弹性不平顺，可有如下结论：1) 橡胶垫减振道床和钢弹簧浮置板道床能有效滤去高于轨道板与板下弹性层(橡胶垫或钢弹簧)共振频率的振动分量； 2) 3 种道床的弹性高低不平顺幅值均在10-12～10-2m，且随着不平顺波长的减小而降低，随着车速的增加而增大； 3) 钢弹簧浮置板道床的弹性不平顺最大值约为其余2 种道床的3.5倍。