移动荷载作用下离散支承浮置板轨道振动响应研究

黄 强，黄宏伟，张冬梅

(1.同济大学 土木工程学院地建下筑与工程系，上海 200092；2.同济大学 岩土及地下工程教育部重点实验室，上海 200092)

随着城市轨道交通快速发展，地铁运行产生的环境振动和噪声问题也引起人们的普遍关注[1-5]，如欧盟实施了CONVURT项目，旨在对地下列车运行引起的环境振动问题进行研究。地铁运行产生的振动和噪声不仅对人们生活和工作环境产生影响，而且还可以通过地层向外传播，诱发地面建(构)筑物的二次振动[6]。目前，这一问题已成为国际公认的七大环境公害之一[7]。

浮置板轨道作为一种减振的轨道形式，目前已广泛用于城市轨道交通线路之中[8-11]。最早英国学者Grootenhuis讨论了几种用于隔绝轨道交通振动向外传播的浮置板结构；Cui[12]以新加坡地铁为例，对比了浮置板轨道和整体式轨道钢轨扣件内力差异，证明浮置板轨道确实具有较好的减振效果。在浮置板轨道计算方面，Hussein等[13]将浮置板轨道等效为双层Euler长梁，推导了连续支承浮置板轨道振动响应解析解；随后Hussein等[14-15]进一步分析了浮置板为离散的情况，浮置板被视作独立的短梁，研究认为浮置板长度增加会使得轨道的刚度增加，产生更复杂振动响应特征；Yuan等[16]也采用文献[13]的双长梁模型分析了浮置板轨道的振动特性，研究认为增加浮置板质量可以提高隔振频率但对改进减振效果不大，增加浮置板支承阻尼和降低其刚度可以提高减振的有效性。Kuo等[17]考虑了车辆与浮置板轨道相互作用，将浮置板轨道视为离散支承的长梁-短梁模型，研究认为低的浮置板支承刚度可以降低轨道振动但会引起大的钢轨挠度，较刚的钢轨扣件和较软的浮置板支承是一种合理的搭配方式。另外，Li等[18]根据浮置板长度的不同，提出了三种浮置板轨道模型，分别将浮置板等效为质量块、长梁和短梁，采用传递函数法比较了三种浮置板模型在简谐振动荷载下的响应差异，研究认为当浮置板长度小于1.8 m时，可以等效为质量块，在1.8～36 m时，应等效为有限长自由梁，大于36 m时，可以等效为长梁。

实际工程中，浮置板的长度并不一致，从不到1米到十几米甚至几十米都有使用，因而对浮置板轨道简化各异，如单梁模型，钢轨简化为长梁，而浮置板简化为连续质量层，适合预制的短型浮置板；双梁模型，将钢轨和浮置板都视为长梁，适合现场浇筑的浮置板；短梁模型，将每块浮置板均视为有限长度的自由梁。尽管各简化模型都具有一定的适用性，但对于其振动响应的差异目前的研究不够，评价的方法也不相同。另外，已有的研究多考虑浮置板连续支承的情况，对离散支承情况分析较少，离散支承浮置板的响应更为复杂，有必要针对离散支承浮置板轨道响应进行分析。本文采用模态叠加法，并结合Runger-Kutta法对不同浮置板轨道振动响应进行对比，分析浮置板长度的影响，最终对浮置板轨道模型选择和减振给出建议，为进一步研究奠定基础。

1 不同浮置板轨道模型解答

参照文献[18],根据浮置板长度的不同，将浮置板简化为质量块、长梁或离散短梁，可以得到三种浮置板轨道模型，分别为长梁-质量块模型、双长梁模型和长梁-短梁模型。通过分析浮置板长度的影响，找出浮置板轨道的临界长度，为今后浮置板轨道模型的选择提供参考。

1.1 长梁-质量块模型

当浮置板长度较短时，可将浮置板视为质量块，此时浮置板轨道简化为长梁-质量块模型，如图1所示。钢轨为离散支承的无限长Euler-Bernoulli梁，抗弯刚度E1I1，N·m2；单位长度质量为m1，kg/m；浮置板单位长度质量为m2，kg/m；钢轨扣件和浮置板支承简化为弹簧-阻尼器单元，间距都假设为0.6 m，刚度和阻尼分别为k1，k2，N/m2；c1，c2，Ns/m2。

长梁-质量块模型的振动方程如下

(1)

其中

(2)

式中：w1为钢轨挠度，w2i为第i个浮置板的位移，共有N个浮置板。

为求解方程(1)，本文采用振型叠加法[19]，将钢轨的挠度表示如下

(3)

式中：Yk(x)、qk(t)是正则振型函数和时间坐标。对于长梁，其振型函数可以采用简支梁的正则振型函数，表达式如下

(4)

式中：L0是钢轨计算长度，m。

经化简，可将偏微分振动方程变换为二阶常微分方程，如下所示

(5)

式(5)可以进一步写成矩阵方程形式

(6)

式中：X=(q1q2…qnmw21w22…w2N)T。

1.2 双长梁模型

当浮置板长度较大时，可将浮置板等效为无限长Euler梁，抗弯刚度为E2I2，N·m2。此时浮置板轨道简化为双长梁模型，如图2所示。

图2 双长梁模型Fig.2 Double long beam model

双长梁模型的振动方程如下

(7)

其中

(8)

同样，采用振型叠加法，钢轨和浮置板的挠度可表示如下

(9)

两者的振型函数表达式分别为

(10)

经化简得到双长梁模型的常微分振动方程如下

(11)

同样，式(11)可以写成式(6)矩阵形式，此时：X=(q1q2…qnmΦ1Φ2…Φnm)T。

1.3 长梁-短梁模型

实际中浮置板为有限长度的自由梁，此时浮置板轨道可简化为长梁-短梁模型，如图3所示。

图3 长梁-短梁模型Fig.3 Long beam-short beam model

长梁-短梁模型的振动方程如下

(12)

其中

(13)

式中：Ls为浮置板的长度，m；w2m为第m个浮置板的挠度，共有n个浮置板；NP为单个浮置板内的扣件或支承数目，N为扣件和支承总数目，N=n×NP。

钢梁、浮置板的挠度表达式为

(14)

式中：nmr、nms分别为钢轨和浮置板的模态数目。浮置板为自由梁，参照文献[20]，其正则振型函数为

Zk(x)=

(15)

式中：系数βk、Ck的取值如表1所示。

表1 短梁振型函数系数Tab.1 Coefficients of mode function of short beam

经化简得到长梁-短梁模型的常微分振动方程如下

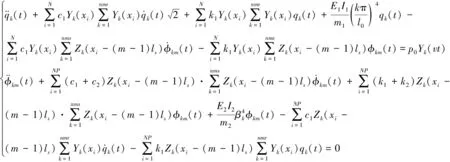
(16)

同样，式(16)可以写成矩阵方程形式，此时X=(q1q2…qnmrΦ1…Φ1nmsΦ2…Φ2nmsΦn1…Φnnms)T。

2 振型叠加法模型验证

利用振型叠加法得到浮置板轨道模型的常微分振动方程组，再利用四阶Runger-Kutta法求解得到轨道的振动响应。为了验证振型叠加法的准确性，以文献[13]中移动荷载作用下连续支承双长梁浮置板轨道模型为例，对比振型叠加法和文献[13]中理论解析结果。验证模型的轨道参数如表2所示。

表2 浮置板轨道参数Tab.2 Parameters of floating slab track

以钢轨挠度和扣件内力为例，计算结果如图4和图5所示。可以看出，采用振型叠加法得到的钢轨动力挠度和文献[13]的理论结果完全一致；钢轨扣件内力除了局部有所差别外，也与解析解结果完全一致，表明采用振型叠加法来计算浮置板振动响应是合理可靠的。

3 不同浮置板轨道模型计算结果

为分析不同浮置板轨道模型的响应差异，选取实际浮置板轨道参数进行动力响应分析。本文采用文献[17]台北轨道交通系统短型浮置板轨道参数，对不同浮置板轨道模型的响应差异以及浮置板的减振特性做进一步分析，轨道参数如表3所示。钢轨为UIC60钢轨，钢轨计算长度及浮置板总长大于100 m，减少钢轨边界截断效应，以满足不同浮置板长度下的计算要求。经过试算，长梁的模态数为80，短梁的模态数为20时，可以保证计算结果的稳定性。

图4 钢轨动力挠度对比Fig.4 Comparison of dynamic deflection of rail

图5 钢轨扣件内力对比Fig.5 Comparison of dynamic force of rail pad

表3 浮置板轨道模型计算参数Tab.3 Parameters of floating slab track

3.1 钢轨和浮置板挠度曲线

三种浮置板轨道模型钢轨挠度曲线如图6和7所示。横坐标距离为离最靠近钢轨中心扣件的长度，挠度为在荷载不同距离处对最靠近钢轨中心扣件点和对应浮置板支承的挠度。从图中可以看出，长梁-质量块模型的钢轨挠度和浮置板挠度都最大，而双长梁模型的挠度则小得多，长梁-短梁模型的挠度则与浮置板长度有关。当浮置板长度为0.6 m时，长梁-短梁模型的挠度和长梁-质量块模型完全一致，当浮置板长度增加到6 m时，长梁-短梁模型挠度则和双长梁模型的挠度曲线较为一致，随着浮置板长度增加，两者挠度曲线差异逐渐加大。因此，就以本文的轨道参数来说，6 m似乎可以看作是浮置板的一个临界长度。理论上讲，长梁-质量块模型和双长梁模型可以视作长梁-短梁模型的两种极端情况，长梁-短梁的钢轨挠度幅值应介于两者之间。因此，从挠度响应差异上看，在选择浮置板轨道模型时，有必要先确定浮置板的临界长度。

图6 钢轨挠度对比Fig.6 Comparison of rail deflection in three floating slab track models

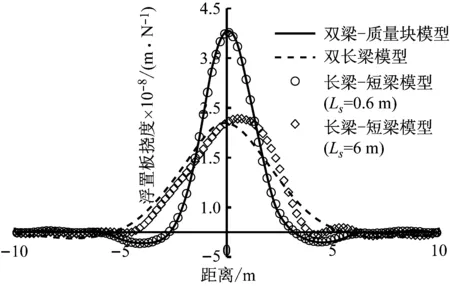
图7 浮置板轨挠度对比Fig.7 Comparison of slab deflection in three floating slab track models

3.2 钢轨扣件和浮置板支承内力

同样对比不同浮置板轨道模型下钢轨扣件内力和浮置板支承内力分布，如图8和图9所示。可以看出，将长梁-质量块模型的钢轨扣件内力最小，而将双长梁模型得到的钢轨扣件内力最大。与此相反，浮置板支承内力则和浮置板挠度曲线规律一致，将浮置板等效为质量块时，浮置板支承内力最大，将浮置板等效为长梁得到的浮置板支承内力最小，长梁-短梁模型的内力计算结果则与长度密切相关。因此，有必要研究浮置板长度的影响，以利于浮置板轨道模型的选择。

图8 钢轨扣件内力Fig.8 Forces in the rail pad in three floating slab track models

图9 浮置板支承内力Fig.9 Forces in the slab bearing in three floating slab track models

3.3 浮置板长度影响

计算不同浮置板长度下长梁-短梁模型钢轨挠度曲线，并对比不同浮置板模型的钢轨挠度和浮置板支承内力，如图10～12所示。可以看出，随着浮置板长度的增加，钢轨挠度会逐渐减少，但下降趋势减缓，钢轨挠度峰值开始趋于稳定。从图11和图12看出，根据本文轨道参数，6 m是浮置板的临界长度。当浮置板长度大于6 m时，长梁-短梁模型的钢轨挠度计算值或浮置板支承内力会降至双长梁模型之下，这种计算结果理论上是不合理的，造成该结果的原因可能是当浮置板长度较大时，短梁的振型函数已经不再适用，否则会引起较大计算误差，此时钢轨与浮置板的相互作用非常近似于两个长梁的相互作用。本文的轨道参数来说，短梁长度的适用范围为0～6 m，在此范围内，应采用长梁-短梁模型进行浮置板轨道的振动响应计算；超过6 m则应采用双长梁模型；当浮置板长度很小时，如0～0.6 m，可以退化为长梁-短梁模型计算，计算结果误差很小。

图10 不同浮置板长度下钢轨挠度曲线Fig.10 Rail deflections from different lengths of floating slab

图11 浮置板长度对钢轨挠度影响Fig.11 Influence of floating slab length on rail deflection

图12 浮置板长度对浮置板支承内力影响Fig.12 Influence of floating slab length on its inner force

4 浮置板轨道减振特性分析

浮置板轨道的主要目的在于减少列车运行引起的环境振动，其减振原理为减少传递至浮置板下卧层的振动荷载。另外，为保证列车行车舒适性，使用浮置板轨道的同时，应该避免浮置板轨道振动引起的钢轨挠度增加。从图12结果来看，增加浮置板长度是一个有效手段，但是当浮置板长度超过临界长度时，其减振提升效果已不明显。因此，当浮置板长度一定时，改变轨道结构其他参数，如钢轨扣件刚度、浮置板质量、浮置板抗弯刚度和浮置板衬垫刚度成为可能的手段。本文以Ls=3 m浮置板轨道为例，分别对钢轨扣件刚度、浮置板质量、浮置板抗弯刚度和浮置板支承刚度的减振效果进行分析，结果如图13～20所示。

图13 扣件刚度对钢轨挠度影响Fig.13 Influence of stiffness of rail pad on rail deflection

图14 扣件刚度对浮置板衬垫内力的影响Fig.14 Influence of stiffness of rail pad on the force in slab bearing

4.1 钢轨扣件刚度的影响

钢轨扣件刚度的影响见图13和14。从图中可见，增加钢轨扣件刚度会显著减少钢轨的挠度，同时引起浮置板支承内力的减小，但较对钢轨挠度的影响效果要小得多。因此，增加钢轨扣件刚度有利于提高浮置板的减振效果，且有利于提高列车行车舒适性。这与文献[17]的研究结论相一致。

4.2 浮置板质量的影响

浮置板质量对钢轨挠度和浮置板衬垫内力的影响如图15和16所示。假设浮置板质量增加不引起浮置板抗弯刚度改变，图中可以看出，单纯增加浮置板质量会引起钢轨挠度和浮置板支承内力的增加，但浮置板质量较大时，钢轨挠度和浮置板支承内力会趋于稳定。因此，可以说，增加浮置板质量不利于改进浮置板的减振效果。这个结论和文献[16]的有所差异，其原因在于文献[16]采用的是双长梁模型，且其考虑的是移动简谐荷载的情况，所以浮置板质量的效果不明显。

图15 浮置板质量对钢轨挠度影响Fig.15 Influence of slab mass on rail deflection

图16 浮置板质量对浮置板支承内力影响Fig.16 Influence of slab mass on the force in slab bearing

4.3 浮置板弯曲刚度的影响

当增加浮置板的厚度时，引起的浮置板的抗弯刚度增加较质量增加会更加明显。图17和18可以看出，增加浮置板抗弯刚度可以有效地改进浮置板的减振性能，同时减少钢轨挠度和浮置板支承内力，一定程度上也抵消浮置板质量增加带来的减振不利影响。因此，增加浮置板抗弯刚度也是提升减振效果和行车舒适性的有效手段。

图17 浮置板抗弯刚度对钢轨挠度影响Fig.17 Influence of flexural stiffness of slab on rail deflection

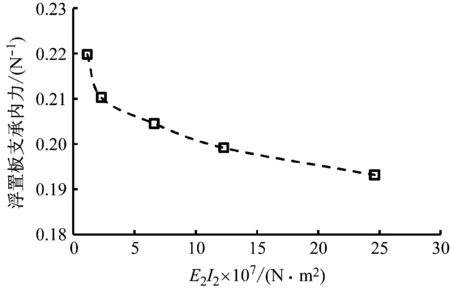
图18 浮置板抗弯刚度对浮置板支承内力影响Fig.18 Influence of flexural stiffness of slab on the force in slab bearing

4.4 浮置板支承刚度的影响

浮置板通常采用橡胶或钢弹簧支承，因而浮置板支承刚度对浮置板减振性能有重要的影响，见图19和20。可以看出，增加浮置板衬垫刚度可以显著减少钢轨挠度，但会引起浮置板支承内力显著增加，引发更大的环境振动。因此，浮置板支承刚度的改变在减振和保证行车舒适性方面是一对矛盾。因此，为改进浮置板的减振效果，有必要适当减少浮置板的支承刚度，而引起的钢轨挠度增加可由其他轨道参数调整来予以抵消，如增加钢轨扣件刚度、浮置板抗弯刚度等。

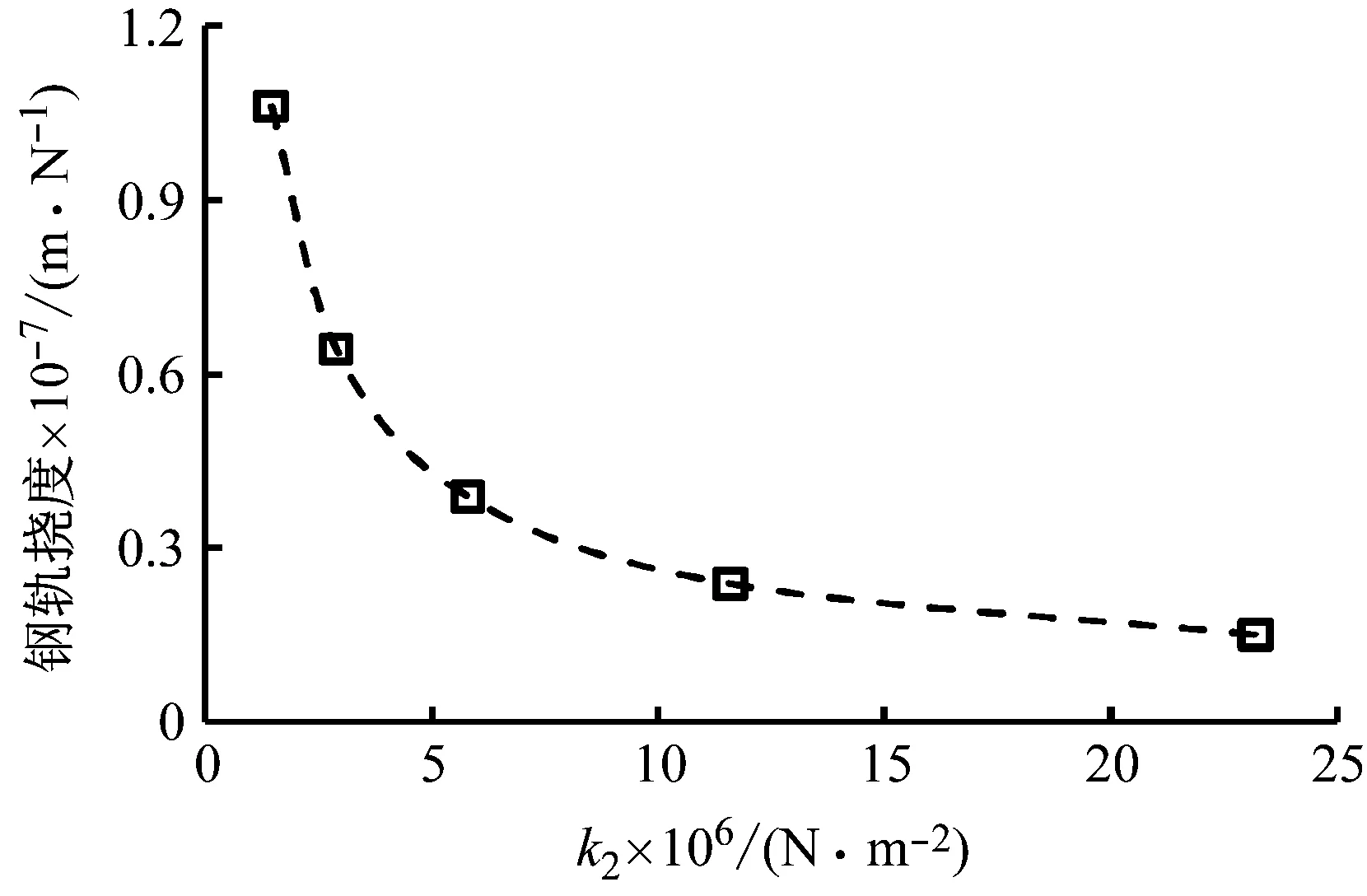
图19 浮置板支承刚度对钢轨挠度影响Fig.19 Influence of stiffness of slab bearing on rail deflection

图20 浮置板支承刚度对其内力影响Fig.20 Influence of stiffness of slab bearing on its inner force

综上所述，增加钢轨扣件刚度和浮置板抗弯刚度既可以减少钢轨挠度又能减少浮置板支承内力；增加浮置板质量则对减振和行车舒适性都不利，增加浮置板支承刚度有利于减少钢轨挠度却引起浮置板下卧层荷载增加。因此，除了增加浮置板的长度外，一个切实可行办法是增加钢轨扣件刚度、浮置板抗弯刚度，适当减少浮置板支承刚度从而既提升浮置板轨道减振特性又满足列车行车舒适性的需要。

5 结 论

本文利用振型叠加法得到了三种浮置板轨道模型的解析解答，在利用数值方法得到了浮置板轨道响应结果。比较了轨道模型的振动响应差异，并分析了浮置板轨道的减振特性，得到以下几个结论：

(1) 长梁-质量块模型和双长梁模型是长梁-短梁模型两种极端情况，实际浮置板轨道响应结果应介于长梁-质量块模型和双长梁模型之间。浮置板存在一个临界长度，当浮置板长度较小时(如0～0.6 m)，可以等效为长梁-质量块模型；当浮置板长度较大时(如大于临界长度)，则应等效为双长梁模型进行计算；否则应等效为长梁-短梁模型。

(2) 当浮置板长度较大时(大于临界长度)，将浮置板视作短梁会引起计算误差，此时短梁振型函数已不再适用，浮置板应整体等效为长梁。

(3) 浮置板轨道减振的改进方法是增加浮置板长度、增加钢轨扣件刚度、增加浮置板抗弯刚度同时适当减小浮置板支承刚度，这样既能保证列车行车舒适性又能减少传递至浮置板下卧层的振动荷载，从而减少地铁运行所引起的环境振动。