齿轮故障诊断的时域同步平均改进算法

揭震国，王细洋*

（南昌航空大学 通航学院，南昌 330063）

0 引言

现代工业设备的结构复杂、工作环境恶劣等，使得故障信号大多信噪比较低，从而极大地影响了齿轮动力传动系统运行状态信息的准确获取及其状态识别。时域同步平均算法是提高齿轮故障诊断振动信号信噪比的有效方法；因此，通常将时域同步平均算法用于齿轮诊断的预处理。许多学者把它应用在信号去噪和提高信噪比的场合[1-3]。时域同步平均算法有基于时标的时域同步平均和基于周期的时域同步平均2种方式。由于存在频率估计误差，基于周期的时域同步平均算法的噪声抑制效果将大打折扣，同时有用特征信号也会有很大的衰减[4]。相比之下，基于时标的时域同步平均降噪效果更佳；但转速存在波动现象使得时标信号不能保证各数据段点数相等，故采取频率跟踪技术以保证数据段点数相等。

罗德扬[5]指出，采用频率跟踪技术以保证在机器转速波动时各数据段点数相等是时域同步平均的关键，主要有3种方法实现频率跟踪，分别为光电脉冲编码发生器、频率乘法器、数据二次采样技术。周晓君[4]为了消除转速波动条件下的累积相位误差，提出了基于特征频率估计的变周期信号时域平均方法，用于抑制振动信号中的噪声。一些学者依据机械振动信号自身的特点，先提取出时标信号，再借助时标信号对数据进行分段平均[6-7]。

和其他需要使用外触发采样装置的频率跟踪方法不同，数据二次采样技术无需外触发设备，而是采用软件手段完成频率跟踪，具有精度高、灵活、可靠等优点。根据Shannon采样定理，若使用sinc函数对离散信号进行重采样，则可准确地恢复出原始信号，于是sinc函数被称为理想插值函数[8]。因而罗德扬[5]、鞠萍华[9]、付海燕[10]、罗欢欢[11]等直接使用sinc函数重采样实现频率跟踪，但他们使用该函数时都基于一个假设，即信号进行无穷项求和。然而，在实际恢复信号的过程中，通常只涉及到有限项求和，因此就会产生一个截断误差，并且sinc函数还涉及到较大的计算量以致其计算速率慢。此时若仍把sinc函数看作是理想的插值核，则会对时域平均的结果产生不利的影响。

针对sinc函数存在重建误差大和计算速率慢的问题，本研究提出三次样条函数代替sinc函数实现频率跟踪的新算法，以期解决这些问题。

1 基本理论

1.1 经典数据二次采样技术

数据二次采样技术[5]是将被分析信号x(t)和时标脉冲e(t)输入双通道A/D变换器，得到长系列的离散信号xn、en；按en包含的脉冲系列，将xn分为若干数据段(p=0,1,2,…,P)。这时，由于转速的波动，各数据段的点数是不相等的。而后，根据各数据段不同的采样点数M(i)，按统一的二次采样点数N，选用不同的采样间隔 Δw(i)=Δt×M(i)/N，自适应地对每一数据段作二次采样，得到点数皆为N的P个数据段。

经典数据二次采样技术通常使用sinc函数进行插值重构，设xn有X个离散点，将信号分为m个数据段，数据段的点数为M(i)，二次采样点数为N，以二次采样间隔Δw(i)对xn二次采样得，重构公式可表示为：

其中，N由式（2）知，按不变的二次采样点数N，根据M(i)，以自适应采样间隔Δw(i)对所有数据段二次采样，就可以实现频率跟踪。

经典数据二次采样技术使用sinc函数时通常基于一个假设，即sinc函数是理想的插值核。理想的sinc函数有2个重要性质，即：

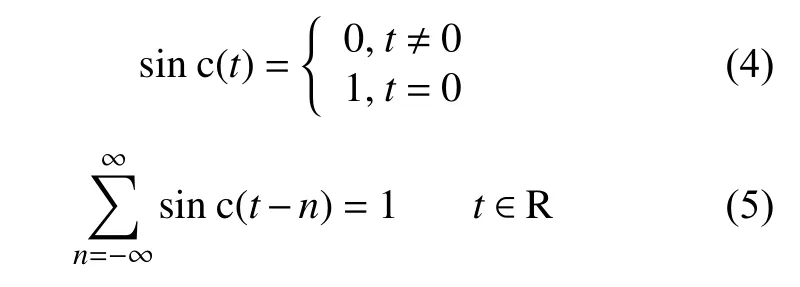
但是在实际应用中，式（5）只能进行有限项求和，并不能完成无限项求和，所以这个假设在实际应用中并不成立，会产生一个截断误差。截断误差的存在使得信号在时域平均时部分故障频率被压制。如果需要得到一个合适的截断误差，则需要很多项求和，这就会带来很大的计算量。因此，时域同步平均采用经典数据二次采样技术实现频率跟踪时，往往在抑制噪声的同时，对故障特征也产生很大的抑制。

1.2 改进算法

为解决sinc函数插值核存在的问题，使用新的插值核替代sinc函数，而新的插值核必须满足3个性质：

1） φ (t)是一个具有紧支集的函数，即存在正实数 M＞0，使得当|t|＞M 时，有 φ (t)=0；

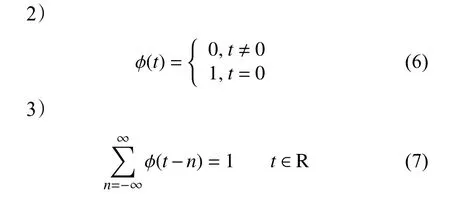
三次样条插值核符合以上3个性质，并且能很好地平衡计算速率和重建精度两方面，是理想sinc函数的合适替代者。采用三次样条插值核代替sinc插值核的表达式为：

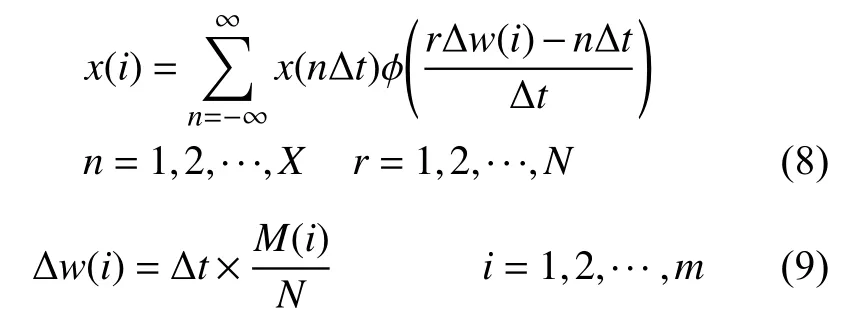
三次样条插值函数 φ (t)可以有多种表达方式，本研究采用的是三弯矩方程[12]。

由于 φ (t)在区间[tj,tj+1]上是三次多项式，故φ′′(t)在[tj,tj+1]是线性函数，可表示为：

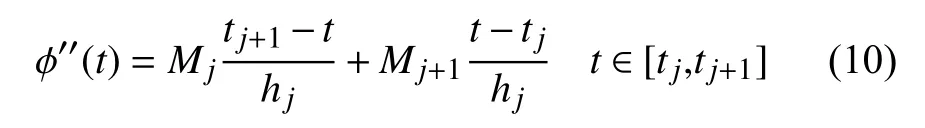
对 φ′′(t)积 分2次 ， 并 利 用 φ (tj)=yj及 φ(tj+1)=yj+1，可定出积分常数。于是得三次样条表达式：

其中，hi=ti+1-ti，取自然边界条件，即

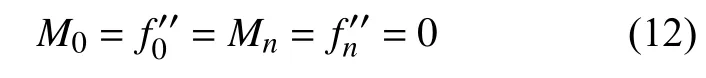
在一定约束下，三次样条函数的具体公式[13]为：

同样符合新的插值核条件的有线性插值核，图1给出了sinc函数、理想sinc函数、线性插值函数和a=-0.5时三次样条函数的频谱对比图。从图1可知，线性插值函数衰减带的旁瓣最大，其衰减速率是三者中最慢的；而sinc函数不仅衰减带上具有较大的旁瓣，还存在低频通频带的过冲现象，说明其不仅衰减速率较慢，还存在较大重建误差。而spline插值函数的衰减速率和重建误差两方面皆优于sinc函数和线性插值函数。因此，spline插值函数是理想sinc函数的合适替代者。

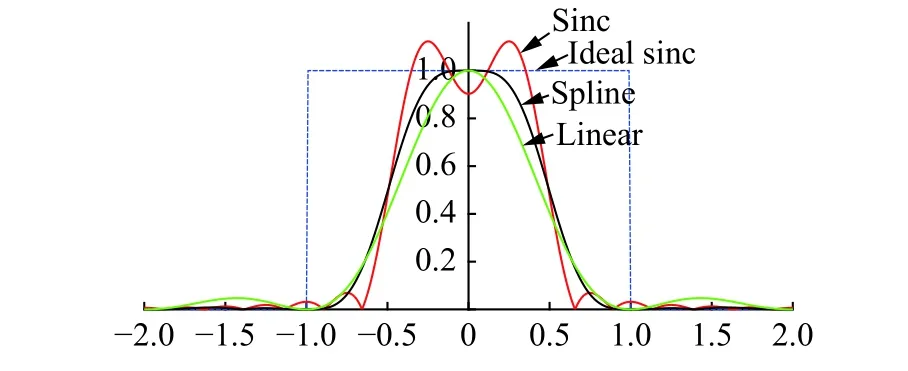
图1 不同插值核的频谱图Fig.1 Spectra of different interpolation kernel

1.3 改进算法的实现

1）按峰值搜索算法搜索时标信号，根据一定的阀值设定最小峰值，如80%Vp(时标信号峰值)。将找到的第一个符合条件的数据置1，也就是第1个脉冲的位置。依次按照数据顺序搜索后面的数据，即可得到脉冲位置序列W={w1,w2,···,wn}。

2）根据脉冲位置序列得到各段数据的采样点数，即M(i)=wi+1-wi。

3）选用合适的N，为保证最终的实际采样频率应大于信号x(t)的带宽的2倍，同时便于谱分析。N需满足M(i)/N＜a/2，且N为基2数，a为原采样频率与信号带宽的比值。

4）根据 Δw(i)=Δt×(M(i)/N),Δt=1/fs，确定二次采样间隔Δw(i)。

5）根据原始信号x(n)、原始采样序列n、原始采样间隔Δt、二次采样序列r、二次采样间隔Δw(i)，利用三次样条插值方法重构一段新的N点等间隔信号x(i)。

6）对m段重构信号x(i)进行时域同步平均得到平均后信号x(r)。

2 仿真信号分析

本研究仿真的是齿轮齿面磨损信号，当齿轮的齿面产生均匀磨损时，在频率成分中产生啮合频率的2 次、3次等高次谐波。

设仿真信号由周期信号和高斯白噪声组成，即：

其中，

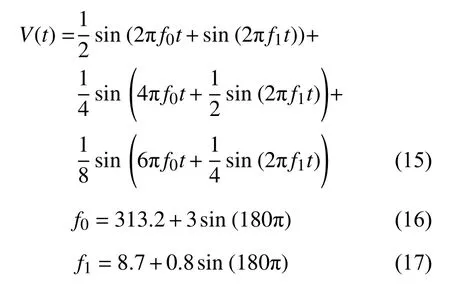
式中：f0为啮合频率，f1为调制目标齿轮的转频，2、3倍频的幅值分别为1倍频的1/2和1/4。啮合频率加入幅值为3的正弦波是为了模拟转速波动。高斯信号N(t)的噪声强度为0.4，SNR为2。仿真时标信号是幅值为4，频率为f1的周期性方波。采样频率fs=20.480 kHz，信号长度X=200 000，313.2 Hz及其倍频为感兴趣频率。

分别采用经典方法和改进方法对仿真信号进行处理。图2分别为仿真原始信号、改进方法和经典方法得到的信号时域图。从图中可知，无论是经典方法和改进方法都能抑制噪声。相比于经典方法，改进方法能更好地抑制噪声。

2种算法的频谱图对比如图3所示。可以看出，经典算法和改进算法对噪声部分和非感兴趣频率部分都能很好地抑制，但改进算法对于感兴趣频率（313.2 Hz及2、3倍频）的削弱程度明显低于经典算法。

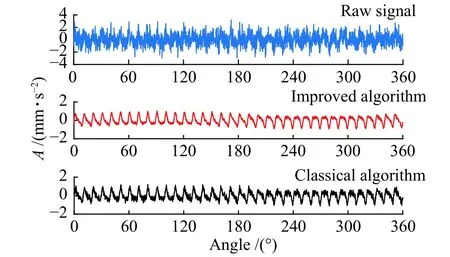
图2 仿真信号时域同步平均后时域对比图Fig.2 Time-domain comparison diagram of simulation signal after TSA

图3 仿真信号时域同步平均后频谱对比图Fig.3 Spectrum comparison diagram of simulation signal after TSA

3 齿轮振动信号分析

3.1 试验装置

实验台如图4所示。行星齿轮箱传动比为4.571。平行齿轮箱为二级传动组成，输入轴主动轮 Z1（齿数29）和中间轴从动轮 Z2（齿数100）构成一级传动，中间轴主动轮Z3（齿数36）和输出轴从动轮Z4（齿数90）构成二级传动。本研究的实验对象为平行齿轮箱的中间轴齿轮。

图4 实验台Fig.4 Experiment rig

电机输入转频为30 Hz，转频范围为29.92～30.00 Hz，无负载，通过安装在平行齿轮箱箱体上的三轴加速度器采集振动信号，传感器安装位置如图5所示。本研究选用传感器2采集的X轴（即目标齿轮径向）信号进行分析。信号长度为655 358，采样 20.480 kHz，二次采样点数为 16 384，平均次数30次。选用转速传感器收集到的转速脉冲信号作为时标信号。

图5 传感器安装位置图Fig.5 Sensor installation location diagram

3.2 信号分析

丁康等[14]指出齿轮故障特征频率通常为啮合频率及其倍频、故障所在轴转频及其倍频。根据式（18）～式（21）可得信号的特征频率[14]，平行二级啮合频率fm2为68.42 Hz。即感兴趣频率为68.42 Hz及其倍频。

分别用经典算法和改进算法对信号进行处理，得到信号时域同步平均后时域对比图（图6）和频谱对比图（图7）。从图6中可以看出，经典算法和改进算法都能达到抑制噪声的效果，对比图6b、图6c可以发现，改进算法可以更好地抑制噪声，并且可以明显看到36个脉冲，这些脉冲正好对应目标齿轮36的齿数。从图7可以看出，经典算法和改进算法对于噪声和非感兴趣频率部分都能起到抑制作用，但改进算法对于噪声和非感兴趣频率部分的抑制更加明显，以及齿轮啮合频率68.3 Hz、2 倍频 136.7 Hz、3 倍频 205.1 Hz的保留效果提高了约10%。

基于Matlab平台进行2种算法的计算速率对比实验，以sinc函数和spline函数的运行时长作为评估指标。改进算法调用spline函数，经典算法调用sinc函数。为了保证实验的有效性，采用了2组信号进行实验，各自的参数如下：

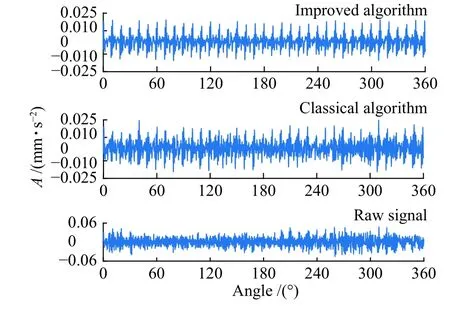
图6 信号时域同步平均后时域对比图Fig.6 Time-domain comparison diagram of signal after TSA

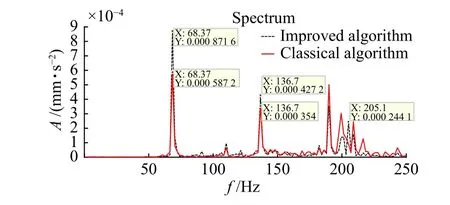
图7 信号时域同步平均后频谱对比图Fig.7 Spectrum comparison diagram of signal after TSA

1）信号 1：信号长度X1=327 679，采样频率fs1=20.480 kHz，各数据段采样点数M1=10 776±100，二次采样点数N1=16 384，数据段m1=30。

2）信号 2：信号长度X2=327 679，采样频率fs2=20.480 kHz，各数据段采样点数M2=2354±22，二次采样点数N2=4096，数据段m2=137。

记录spline函数、sinc函数的运行时间，各函数的运行时间如图8所示。从图中可以明显的发现：无论是信号1还是信号2，sinc函数的运行时间都长于spline函数，这是因为spline函数重建所需的计算资源o(n)远小于sinc函数的o(n2)。同时还可以发现，在相同信号长度和采样频率下，信号1的函数所用时长明显大于信号2，这是因为信号1完成sinc函数重建过程需要m1×N1×M1的计算量远大于信号2的m2×N2×M2。以上验证了改进算法较经典算法提高了计算速率。

4 结论

1）提出三次样条函数代替sinc函数实现频率跟踪以解决转速波动对时域同步平均的影响，研究三次样条函数与sinc函数之间重建误差和计算速率的问题，采用仿真信号和齿轮振动信号验证改进算法。

图8 各函数运行时间图Fig.8 Running time diagram of each function

2）相比于经典TSA算法，改进算法的时间复杂度由平方阶降为线性阶，抑制了噪声，齿轮故障特征频率的识别效果提高了约10%。