基于模态振型的圆截面梁裂纹识别等高线法

吴兴意，刘文光*，戴文柯

（南昌航空大学 航空制造工程学院，南昌 330063）

梁是工程领域的基本构件之一。梁在设计制造、装配维修和使用操作过程中，容易在表面形成凹坑、裂缝等缺陷。加之工作条件严苛和服役环境的恶劣作用，以及材料的老化和疲劳效应等诸多因素，极易导致梁构件发生缺陷或损伤。按照美国军方提出的损伤容限设计理念，任何材料内部都有一定程度的缺陷或损伤，且最主要的损伤模式是裂纹[1]。裂纹的萌生和扩展不仅会削弱梁的承载能力，而且会改变梁的振动特性。尤其是当弹性梁引发共振运动时，梁上裂纹扩展十分迅速，严重时导致梁的断裂破坏。为了提高弹性梁的安全可靠性，越来越多的研究者关注梁的裂纹识别技术。

近几十年来，研究者提出了基于振动信号的裂纹识别方法，该方法的基本原理是将待识别构件看作是刚度、质量和阻尼组成的系统。当系统出现损伤时，系统的刚度就会发生改变，致使整个系统的振动特性发生改变。利用损伤前后系统模态频率的变化规律，Cawley、Willian等[2-3]提出了基于模态频率的损伤位置识别方法。在推导单边裂纹悬臂梁固有频率方程的基础上，Liu等[4]利用实测固有频率与计算固有频率误差的最小值，提出了一种确定裂纹深度和裂纹位置的方法。利用多项式模拟呼吸式裂纹梁的刚度变化规律，刘文光等[5]研究了呼吸式裂纹梁的振动特性，提出了一种基于固有频率的呼吸式裂纹梁损伤识别等高线方法。在研究框架结构梁柱节点振型平移和振型转角敏感性系数的基础上，李林等[6]提出了一种基于转角振型变化的损伤位置识别方法。为了解决噪声的干扰性，Cao等[7]研究了基于振型曲率的含多裂纹悬臂梁损伤识别方法。引入对结构损伤极为灵敏的模态柔度矩阵，邱飞力等[8]研究了以模态柔度矩阵为目标函数的损伤识别方法。利用无损状态下的简支梁和含裂纹简支梁之间的广义柔度曲率，Li[9]研究了基于广义柔度矩阵的损伤识别方法。利用残余应力向量定位潜在的裂纹损伤，Ricles等[10]应用损伤前后残余应力向量的变化识别了损伤的位置与程度。使用模态频率、振型和频响函数作为指标，潘晓威[11]研究了平面钢架结构的损伤识别技术。利用不同幅值激励下高频频响函数不同的特性，闫少文等[12]提出了一种基于非线性高频频响函数的无基准疲劳裂纹损伤识别方法。基于结构损伤前后单元模态应变能的变化，Chen等[13]提出了损伤识别模态应变能法。基于应变与位移之间的关系，周计祥等[14]研究了应变模态与模态振型的转换关系，并应用应变模态代替模态振型识别了损伤的位置。结合参数化建模和神经网络算法，李中志[15]提出了以模态频率变化为损伤指标的含裂纹轴损伤识别方法。

尽管研究者提出了诸多基于振动特性的裂纹识别方法，但在工程实践中因裂纹损伤而引起的事故仍时有发生。究其原因，现有的裂纹识别方法精度和适用范围有限。本研究以常见的圆截面梁为研究对象，基于有限元理论将圆截面梁离散为若干单元，在推导无裂纹和含裂纹单元刚度的基础上，求解含裂纹圆截面梁的模态振型和模态频率响应面，研究一种基于模态振型的裂纹损伤识别方法。

1 裂纹顶端的应力强度因子

以图1所示的含裂纹圆形梁为例，其长度为L，圆截面的半径为R，裂纹到固定端的距离为zc，裂纹深度为a。

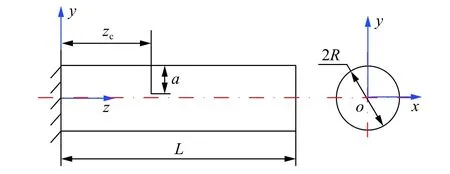
图1 含裂纹圆截面梁模型Fig.1 Model of a cracked circular cross section beam

如图2所示，由于裂纹的存在，裂纹位置圆形截面的中性轴会发生偏移。偏移距离e的计算表达式为：

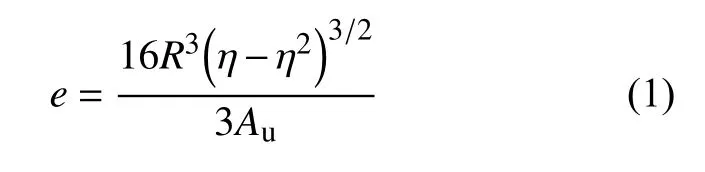
式中：η为裂纹深度比，η=0.5a/R；Au为无裂纹位置梁横截面面积。

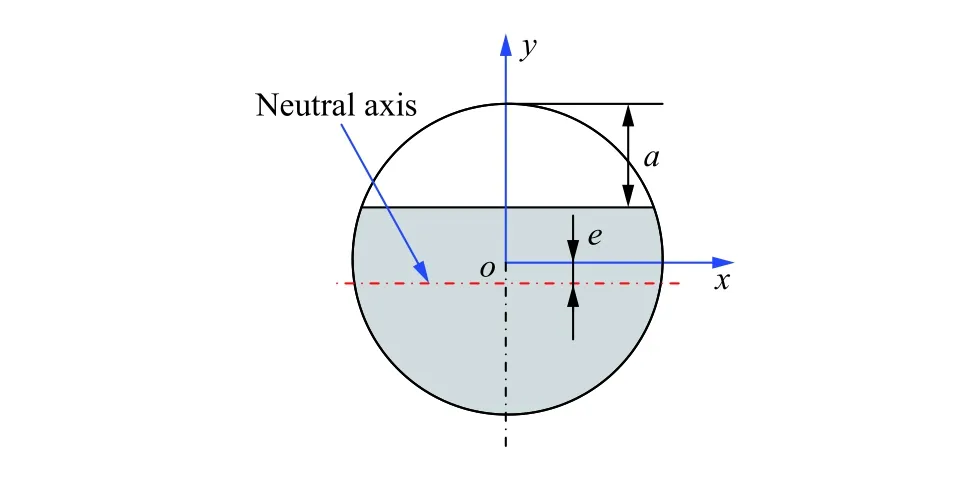
图2 裂纹截面中性轴偏移图Fig.2 Neutral axis offset diagram of cracked section

假设梁分别受到纯轴向拉力N、纯弯矩M或纯剪力S时，由Kienzler和Herrmann理论[16]，可推导出裂纹顶端的应力强度因子表达式分别为：

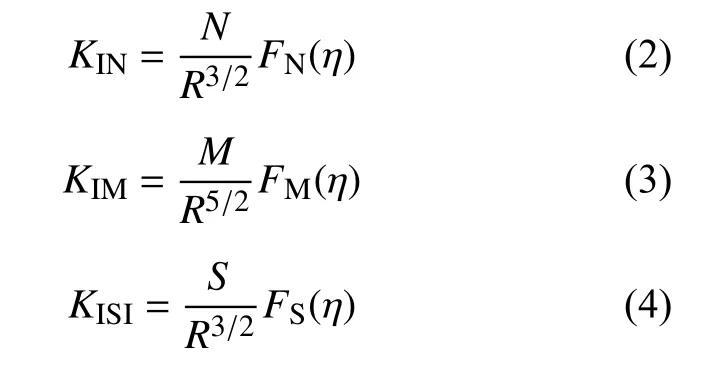
其中，

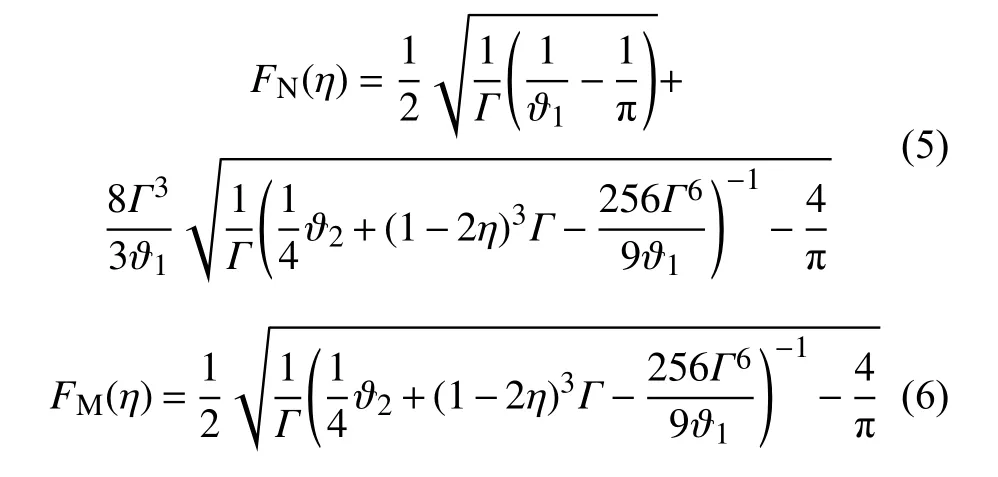
2 单元的刚度矩阵

将图1所示的含裂纹圆截面梁离散为长度为l的一系列梁单元。对于长为l的无裂纹梁单元，当单元受到弯矩M、剪力S和轴向拉伸N时，应变能的大小为：

式中：E为弹性模量，I为圆截面梁的截面惯性矩，μ为梁的剪切模量。

基于卡氏定理，梁的应变能可以表示为关于力的函数，则位移可表示为应变能在该方向上关于力的偏导数，因此梁单元节点的柔度系数cij可表示为：

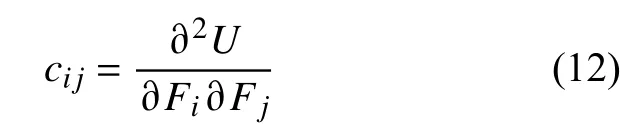
由式(11)、式(12)可推导出无裂纹单元梁的柔度矩阵cu表达式为：

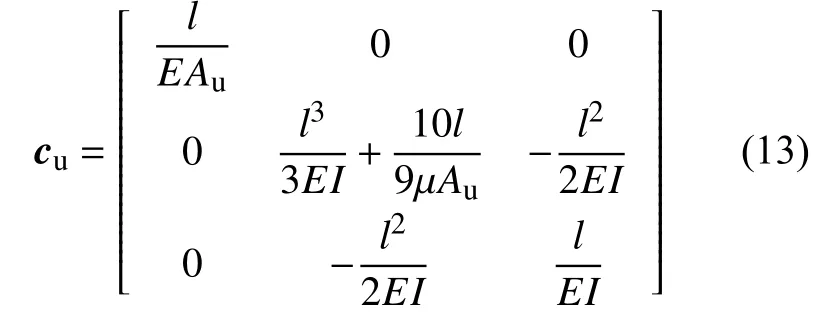
根据柔度法推导刚度矩阵的理论[17]，可得无裂纹梁单元的刚度矩阵Ku为：

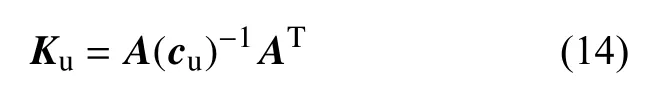
式中：A是节点到单元的坐标变换矩阵，AT是A的转置，表达式为：

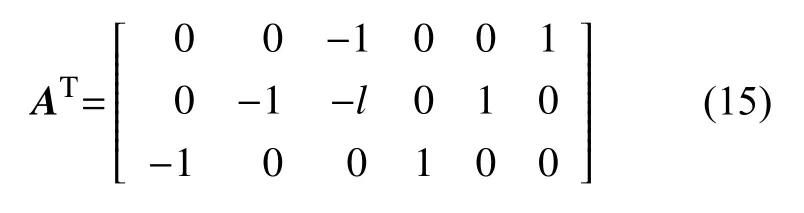
如图3a所示的长为l、半径为R的圆截面含裂纹梁单元，假设用3个分别承受纯轴向拉力、纯弯矩和纯剪力的弹簧模拟其裂纹截面，连接2个理想的光滑圆截面梁模拟其物理属性。建立如图3b所示的直角坐标系，图中a为裂纹深度，b为裂纹宽度。将裂纹截面分割为宽度无限小，即dy和dH的2块薄板。Y为纵向薄板距y轴的距离，h为纵向薄板的长度，H为纵向薄板最高点到裂纹顶端的垂直距离。

根据式（12），含裂纹梁单元受到轴向拉伸力、弯矩和剪力时的局部柔度系数为：

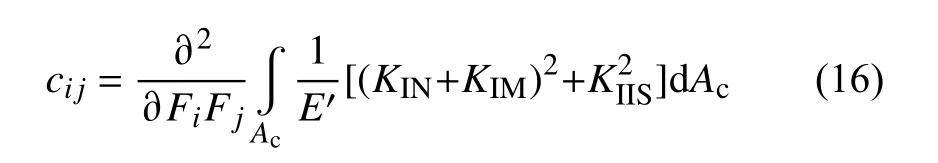
式中：Ac为裂纹表面面积，E′=E/(1-v2)，v为泊松比。

由式(16)可推出含裂纹梁单元节点的柔度矩阵cc为：

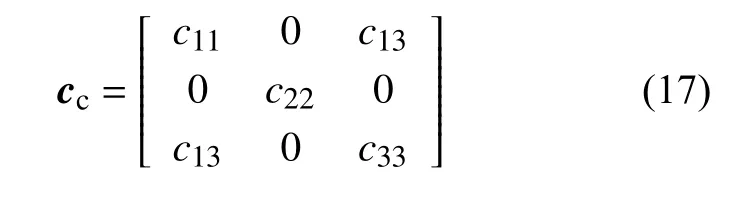
其中：

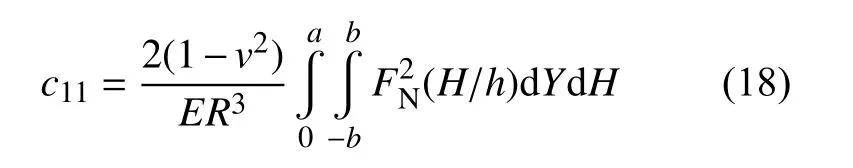
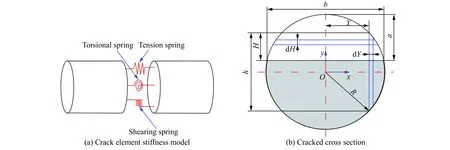
图3 裂纹单元模型Fig.3 Cracked element model

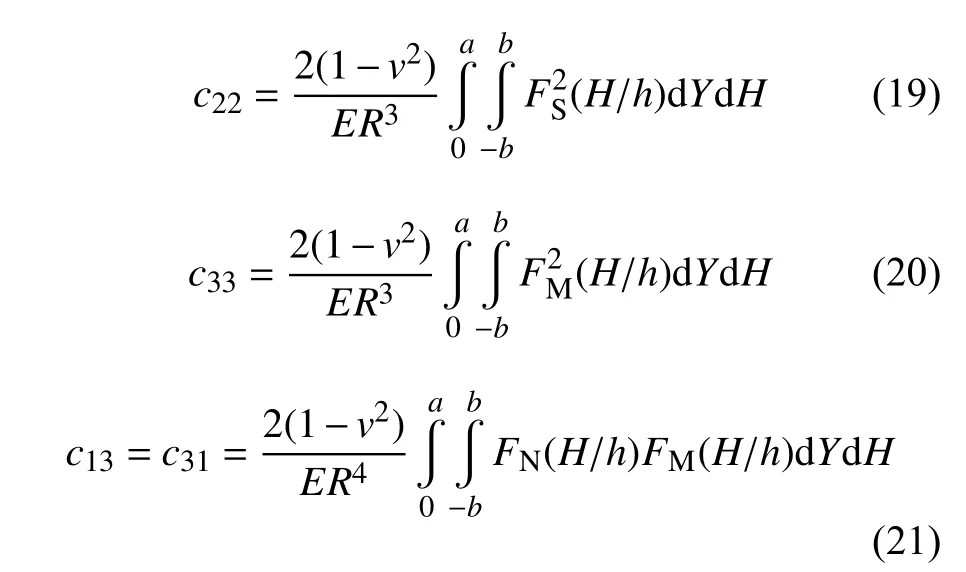
根据柔度法推导刚度矩阵的理论[17]，可求得含裂纹梁单元刚度矩阵Kc为：

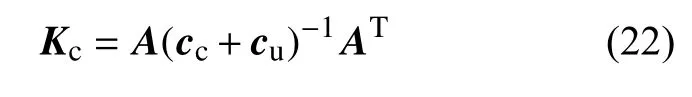
3 含裂纹梁的振动方程

将离散单元的单元刚度矩阵组装得到含裂纹梁的总刚度阵，可推导出含裂纹圆形截面梁的自由振动有限元微分方程：

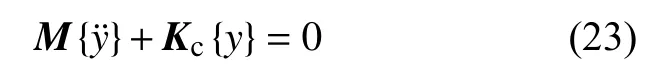
其中，

求解自由振动方程(23)，可得到含裂纹圆截面梁的特征值和相应的特征向量。提取表征裂纹梁弯曲变形的向量，并按节点顺序依次排列，可分析梁的弯曲模态振型，它表明裂纹梁的挠度变化规律。同理，提取表征梁转角变化规律的向量，也可以得到类似于弯曲模态振型的规律曲线，即转角模态振型。转角模态振型表示第i阶自由振动时含裂纹梁的每个节点的转角变化。

假设圆截面梁的材料属性：弹性模量E=2.01×1011Pa、泊松比ν=0.3、材料密度ρ=7.9×103kg/m3。梁的长度L=1 m，梁单元长度l=0.025 m，截面半径R=0.01 m。

图4探讨了单裂纹和双裂纹时，裂纹深度比与裂纹位置比对转角模态振型规律的影响。结果表明，裂纹位置和裂纹深度对转角模态振型有重要影响。在裂纹位置处，不管是单裂纹还是双裂纹情况，转角模态振型曲线均出现突变，而且突变的距离与裂纹位置、裂纹深度皆有一定的关系；因此，可以借助梁的弯曲转角振型识别裂纹位置和裂纹深度。虽然转角振型可以准确地识别出裂纹位置，但是对裂纹深度无法定量，还需借助转角突变的响应面和等高线法来识别。

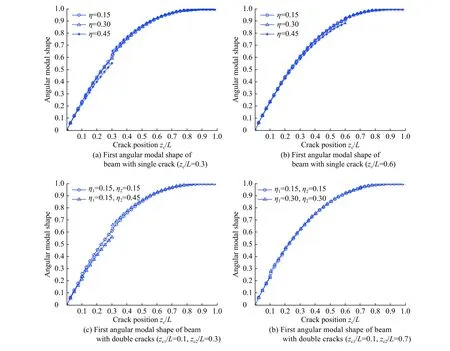
图4 圆截面梁转角模态振型Fig.4 Angular modal shape of a circular cross section beam

4 裂纹识别方法

为了将转角模态振型应用于梁的裂纹识别中，将转角模态振型曲线的突变数值dci定义为：

式中：θc+1、θc表示突变位置处两节点的纵坐标。

以梁的裂纹位置比和裂纹深度比作为自变量，裂纹参数与裂纹梁转角模态振型突变数值的关系式为：

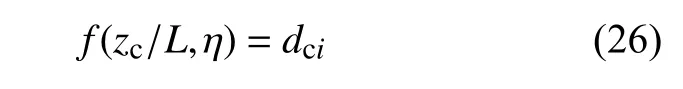
式中：zc/L为裂纹位置比。

求解关系式（25），可分析不同裂纹位置比、不同裂纹深度条件下，单裂纹圆截面梁的转角模态振型的突变值，结果如图5所示。

结果表明，转角模态振型的突变dci和裂纹位置、裂纹深度之间具有一定的映射关系，而且前三阶突变数值的响应曲面皆不相同。对于第一阶突变响应曲面，越靠近梁固支端突变数值就越大；对于第二阶突变响应曲面，当裂纹位置比等于0.52且裂纹深度比等于0.5时突变最大；对于第三阶突变响应曲面，当裂纹位置比等于0.70且裂纹深度比等于0.5时突变数值最大，当裂纹位置比等于0.30且裂纹深度比等于0.48时突变数值最低。

结合前三阶模态振型突变响应和等高线理论，可识别圆截面梁的裂纹位置和裂纹深度，识别流程如图6所示。

图5 前三阶模态振型突变响应曲面Fig.5 Response surface of the first three modal shape

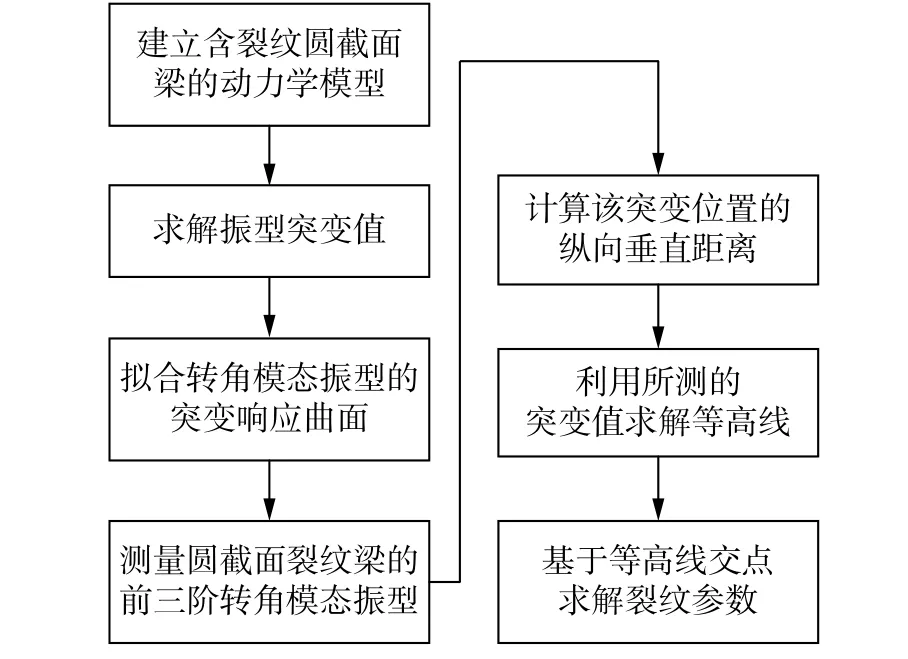
图6 裂纹识别流程图Fig.6 Flowchart of crack identification

5 裂纹识别算例

设计表1所示6种裂纹工况。工况1～3是单裂纹情况，工况4～6是双裂纹情况。结合式（24）计算不同工况下梁的前三阶转角模态振型突变数值。将突变数值代入前三阶模态振型突变响应曲面中，可得到对应的等高线。等高线交点的横坐标则为裂纹的位置比，纵坐标为裂纹的深度比。

如图7所示，单裂纹情况下，3条等高线都严格交于一点，其交点的横坐标为预估的裂纹位置比，而其纵坐标为预估的裂纹深度比。表2所示的识别结果表明，每组裂纹工况的横纵坐标都非常准确地反映了裂纹位置比与裂纹深度比，结果证明转角模态振型的突变等高线法对单裂纹圆截面梁的损伤识别来说是可行的。

如图8所示，双裂纹情况下，3条等高线都并未严格交于一点，而是3条曲线两两相交，并形成一个小三角形区域，通过计算找到此三角形区域的形心位置，并以该形心位置的横纵坐标表示梁构件的裂纹位置比和裂纹深度比。表3所示的识别结果表明，该方法对圆截面梁的双裂纹识别精度非常高。对于裂纹深度比的预测，最大误差不超过2%；对裂纹位置比的预测，最大误差不超过2%。这从理论上证明了转角模态振型的突变等高线法对于含双裂纹圆截面梁的损伤识别来说也是可行的。

表1 不同工况下前三阶模态振型突变值Table 1 Mutation of the first three modes under different cases

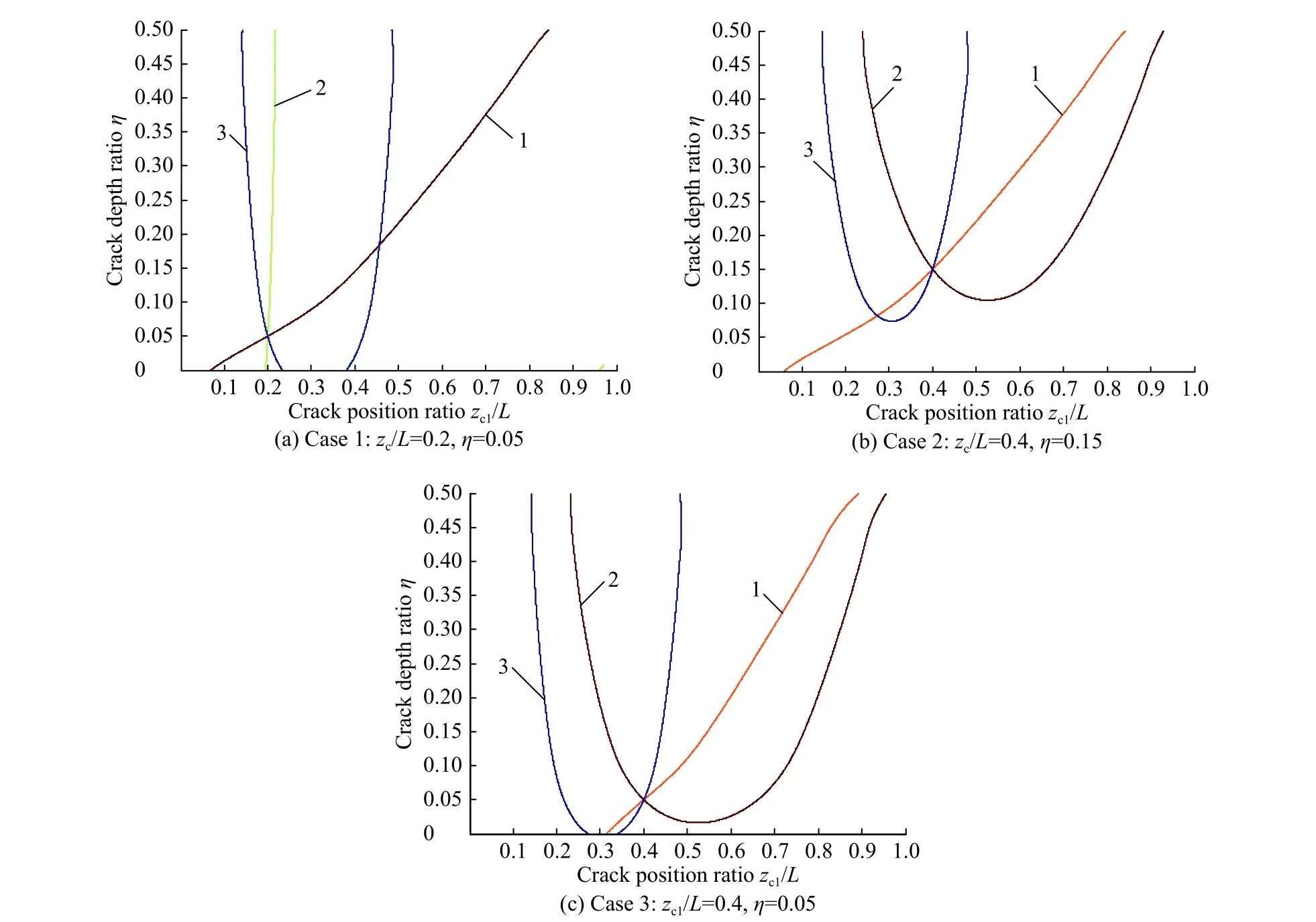
图7 单裂纹等高线图Fig.7 Contour line of single crack

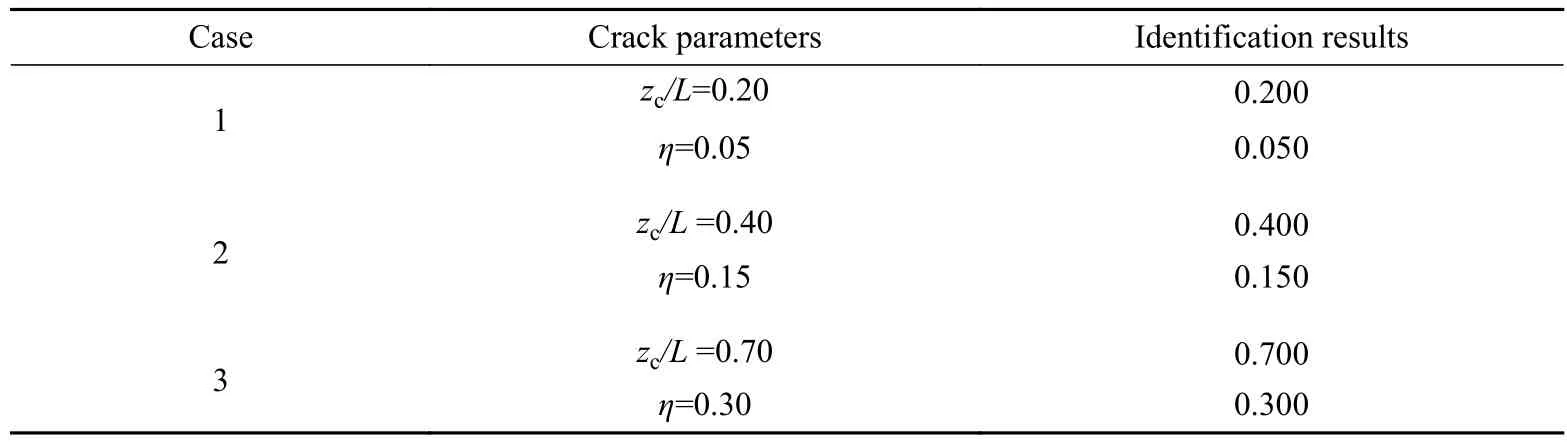
表2 单裂纹梁裂纹参数识别结果Table 2 Identification results of crack parameters for single cracked beam

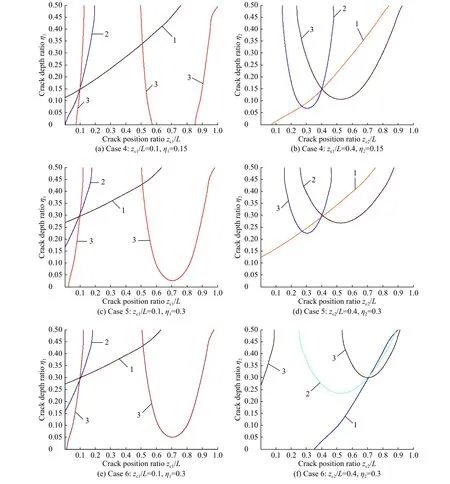
图8 双裂纹等高线图Fig.8 Contour line of double cracks

6 结论

1）转角模态振型的突变值dci对裂纹位置和裂纹深度非常敏感，随着模态阶次的上升，它对裂纹工况的敏感度也会上升，且前三阶突变响应曲面皆不相同。

2）以单、双裂纹圆截面梁为对象，以转角模态振型的突变为损伤识别指针，提出了基于转角模态振型的圆截面梁裂纹识别等高线法。

3）单裂纹圆截面梁裂纹识别时，裂纹深度和裂纹位置的预测结果误差为0；双裂纹圆截面梁裂纹识别时，裂纹深度识别误差不超过2%，裂纹位置识别误差不超过2%。

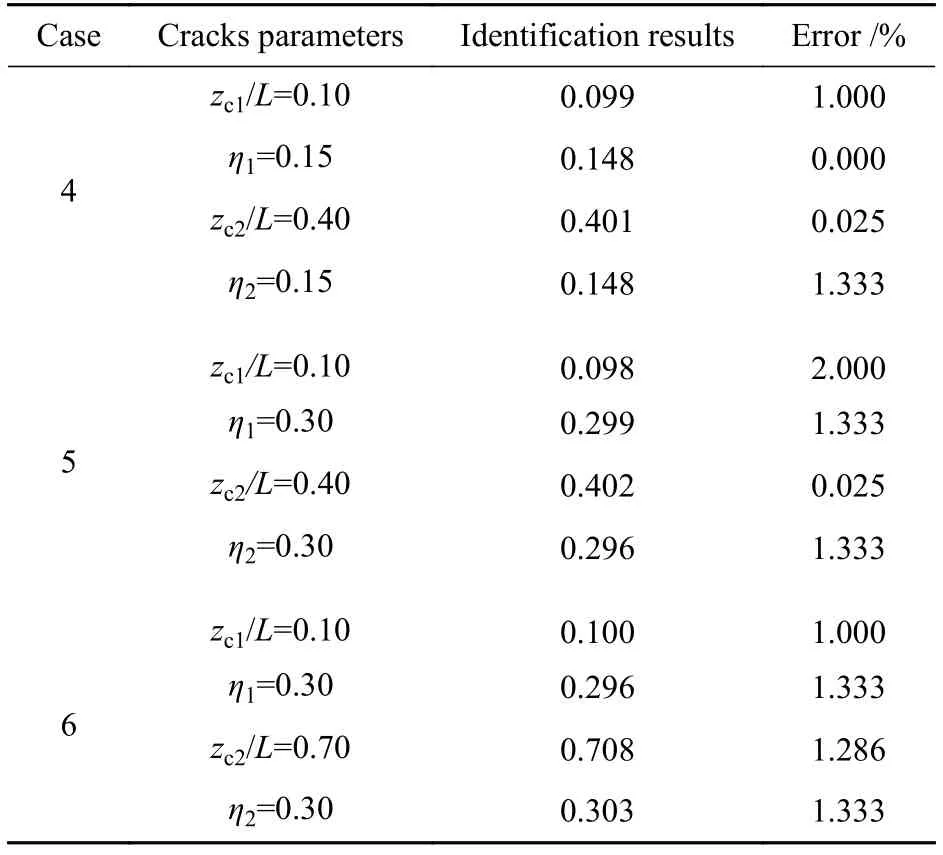
表3 双裂纹梁裂纹参数识别结果Table 3 Identification results of crack parameters for double cracked beam