追本溯源 演绎精彩
——2019年清华大学自主招生第13题寻解之旅
陕西 李 歆
大学自主招生是深化高校招生制度改革的一项重要举措,也是促进中学素质教育全面发展的有效途径.大学自主招生数学试题往往具有难度大,思路活,方法巧等特点,对大学选拔优秀学生和中学数学教学具有一定的方向性和指导性.研究大学自主招生数学试题,从命题背景、解题思路以及方法策略等方面进行深入思考,并站在学生的视角对问题进行解前分析和解后点评,让更多的学生不因遇到大学自主招生试题而烦恼,让更多的学生与大学自主招生试题结为好友,从而在大学自主招生考生中脱颖而出,应该成为广大教师教学的一条专业成长之路.
一、看似简单,实则不易的考题
1.试题呈现
问题1.(2019·清华大学自主招生·13)若正实数a,b满足ab(a+8b)=20,则a+3b的最小值是________.
此题看上去与普通问题没有区别,但思考起来却不是很顺利,对考生分析和解决问题的综合能力要求较高.
2.解法探寻
由于已知条件中含有三次式的结构,而所求问题式只是一次式的线性结构,不能将已知条件中的两个变量单独分离出来,因此用常规的解题工具——均值不等式难以找到出路.注意到所求问题式是一次式,不妨借助换元法,将所求问题式看成一个新的变量,然后利用函数与方程思想试一试.
寻解1:令t=a+3b,则t>0,将a=t-3b代入已知条件,整理得15b3-2tb2-t2b+20=0 (1),
由题意可知,三次方程(1)有正实数解.
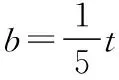




故a+3b的最小值是5.
点评:此解通过换元之后,巧妙地利用导数这个解题工具,以三次方程(1)的正实数解为主线,使问题得以圆满解决,但纵观这个解法,知识含量和思维空间都比较大,一般学生很难理解.同时,这种解法有一个致命的弱点,就是所求问题式必须是线性的,如果将所求问题式换为非线性的,比如二次式a2+3b2,那么这种解法就会失效.况且,作为一道填空题,这种解法似乎有“小题大做”之意.因此,探寻其他解法,不仅很有必要,而且十分有意义.
二、追本溯源,从基础题做起
1.一道基础题
问题2.已知正数a,b满足ab(a+2b)=2,则a+b的最小值是________.
很显然,问题2与问题1十分相似,只是已知条件和所求问题式中的“线性系数”不同而已.对于问题2,如果按照问题1的解法去处理,则显得复杂一些.因为把已知条件稍作变形后,就会得到b(a2+2ab)=2,这时等式左边括号里面恰好是(a+b)2展开式中的前两项,由此可以获得如下解法.
1.1 一种漂亮解法

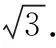
点评:由于问题1和问题2中“线性系数”的差异,导致问题1无法用问题2的方法完成,但问题2的解法却意外的给了我们一种启示,就是用平方法处理线性最值问题,即在已知条件下,如何快捷、高效地处理二次齐次式ma2+nab+kb2的最值问题.
1.2 一种错误解法
有位学生在解问题2时,将已知条件也作了变形,结果却得到了下面的错解.



2.几道变式题
2.1由错误解法引发的变式
在数学解题过程中,学生出现错误是很正常的一件事,在这种情况下,教师切不可轻易地放弃学生的解题思路,强制要求学生按照教师提供的方法来完成解题,那样往往会阻碍学生思维的发展,甚至扼杀学生的创造性思维.因此,教师要善于从学生出现的问题中辩证地分析错因所在,做到因势利导,对症下药,这样才能准确医治学生的“思维伤口”,引领学生思维沿着正确的方向前行.
可以看出,上面这位学生的解题方向值得肯定,导致解法错误的根源在于等号成立的条件前后不一致,如果改变一下已知条件和所求问题,那么会怎么样呢?由此引发出变式1.
变式1.已知正数a,b满足ab(a+2b)=10,则a2+5ab+b2的最小值是________.


故a2+5ab+b2的最小值是15.
点评:此解法与上述错解的过程几乎完全一样,只是某些式子的结构不同,由此说明,在学生错误解法的背后的确隐藏着可以借鉴的和有用的东西,值得教师在教学中加以正确引导,让学生学会找错和改错,从而在错误的源头上彻底清除学生的思维障碍,打通走向成功的希望之路.
2.2改变所求问题式的结构引发的变式
对于变式1,如果已知条件不变,改变一下所求问题式的结构,那么解法会改变吗?
变式2.已知正数a,b满足ab(a+2b)=10,则13a2+17ab+7b2的最小值是________.
容易发现,继续沿用变式1的解法是徒劳的,让我们的思路往回走,面对问题2的解法想一想,能否得到启示呢?


故13a2+17ab+7b2的最小值是75.
点评:把所求问题式进行拆项处理,并将(1)式和(2)式代入后,则巧妙地消去了ab,从而使下一步再拆项水到渠成,同时为均值不等式的运用搭建了平台.
变式3.已知正数a,b满足ab(a+2b)=10,则2a2+2ab+b2的最小值是________.
与变式2相比较,所求问题式的各项系数变小了,按理来说求解应该方便一些,但事实恰恰相反,直接用变式2的解法,对所求问题式进行拆项处理是行不通的,我们不妨将问题式各项的系数变大一些,则可以求解.


故2a2+2ab+b2的最小值是10.
点评:以上三种变式,已知条件相同,只是所求问题式的各项系数发生了变化,然而入手时的思路却在处理细节上有所不同,由此从几个不同的解题视角上,反映了二次齐次式ma2+nab+kb2的解题策略,揭示了“细节决定成败”的解题内涵.
三、条件成熟,优美解法登台
1.问题1寻解出彩
通过对上面的基础题问题2以及三个变式的解法研究,问题1的第二次寻解已经浮出水面,只需要将变式3的解法作一些数字修改即可.


故a+3b的最小值是5.
点评:很明显,寻解2比寻解1要简洁得多,而且寻解2仅仅用到了代数式的变形、平方、配项系数、拆项以及均值不等式,这些都是处理代数最值问题最常用的解题方法和基本工具,是数学教学中最为理想也是众所期盼的解题途径,因此,寻解2充分彰显了数学解题基本方法的魅力和价值所在.
2.问题1的拓展变式
受问题1寻解2的启发,在已知条件不变的情况下,将所求问题式变为二次非齐次的形式,可以得到以下两个变式.
变式4.若正实数a,b满足ab(a+8b)=20,则a2+15ab+21b2+5a的最小值是________.


故a2+15ab+21b2+5a的最小值是65.
变式5.若正实数a,b满足ab(a+8b)=20,则a2+5ab+8b2+b的最小值是________.

故a2+5ab+8b2+b的最小值是23.
点评:由于所求问题式变得复杂一些,因此变式4和变式5相对于问题1又增加了难度,但是有了问题1的寻解2作为参考,以及问题2的三个变式精彩解法的能力提升,处理变式4和变式5便轻车熟路.
四、不忘初心,研究尚在路上
“问题是数学的心脏”,解决问题就是对心脏的维护和保养.一个经典数学问题的诞生,往往凝聚着命题者潜心研究和反复实践的水平和智慧,对数学教学具有不可估量的作用.从问题2到问题1,虽然题型结构没有发生改变,只是将已知条件和所求问题式中的“线性系数”作了简单地调整,但解决问题的策略却在细节上发生了质的变化和飞跃,单凭机械地模仿和借用问题2的解法处理问题1只能是“望洋兴叹”,由此说明从问题2到问题1的解题历程还很遥远.因此,在数学教学中,对问题2的处理如果就题解题,没有后续的变式和教学,那么学生的思维就会被禁锢、被滞留,当问题1出现时就会“似曾相识”,却“望而生畏”.因此,在数学教学中,教师要不忘初心,牢记研究永远在路上,做问题变式及其教学的领路人,不断开启学生的思维智慧,在教学路上让变式教学熠熠闪光.像上面的问题2,在顺利完成解法之后,再进一步地做变式和拓展研究,通过变式1、变式2和变式3的教学,不仅让学生从方法角度掌握此类最值问题的解决策略和思维链条,也让学生从探究领域感悟到数学经典问题的产生背景及其相互关系,当问题1及其变式出现时,思维就会跟着感觉走,在不知不觉中进入到“众里寻她千百度,蓦然回首,那人却在灯火阑珊处”的思维境界,从而实现由基础知识题到能力水平题的思维大提升和大跨越.

