数形结合思想方法应用举例

陕西 侯有岐

数形结合思想是最重要的数学思想之一，“数”和“形”是对同一个事件描述的两种不同的形式，两者相辅相成，各有优点，但其反应的本质相同.本文主要对“形”的认识展开探讨.在实际教学过程中发现，学生对“形”的了解很多时候仅停留在表面的认识，但只要认真分析，问题就很容易解决.

一、考点回顾

在近几年的高考试题中，观数思形、利用数形结合思想解题是高考数学中解决部分函数选填压轴题时常用的解题技巧之一，这也是数形结合思想的最基本应用.对于某些函数最值问题，有时候通过求导数、判断函数单调性的处理策略而无力解决时，我们不妨观数思形，从图象的角度来思考分析，可以通过观察函数图象，给待求式赋予一定的几何意义，从而解决问题.本文通过实例，展示观数思形、巧妙转化，利用数形结合思想和转化思想快速找到解题思路，从而顺利解决函数最值问题.

二、典例剖析

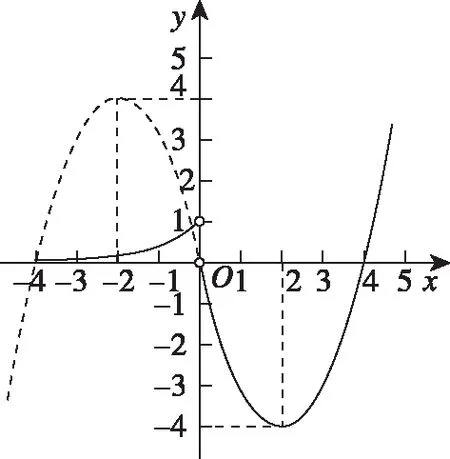
【例1】已知关于x的函数y=(x-a)2+(ex-a+1)2(a∈R)的最小值为m(a)，求m(a)的最小值.

思路分析：此题并非常规函数类型，初步想法是可以通过求导数，然后判断函数的单调性，以此求出函数的最小值.对函数求导得y′=2x-2a+2e2x-2(a-1)ex，我们发现在求解y′=0时，遇到非常大的困难，这样函数的单调性就无法判断，不得不终止这种想法.那么，换个角度思考，还有其他的解法吗？仔细观察函数的表达式之后，可以发现函数表达式是由两个完全平方式构成，自然联想到平面上两点之间的距离公式，于是可以尝试一下将问题转化成求P(x,ex),Q(a,a-1)两点之间的最短距离的平方.

解法一：不妨设P(x,ex),Q(a,a-1)，则y=|PQ|2，且点P(x,ex)为函数y=ex图象上的一个动点，点Q(a,a-1)为直线y=x-1上的一个动点，如图所示，那么PQ何时最短呢？

可以将直线y=x-1向曲线y=ex方向平移，直至与曲线y=ex相切，则切点即为点P，过点P作直线y=x-1的垂线段，垂足为Q，此时PQ最短，如图所示.

( )

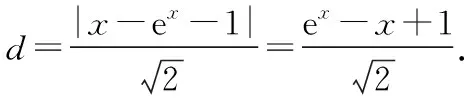
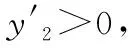
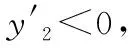
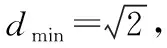
C.e D.3

解法一：不妨设P(a,b),Q(c,d)，则(a-c)2+(b-d)2=|PQ|2，且点P(a,b)为函数y=x2-lnx图象上的一个动点，点Q(c,d)为直线y=x-2上的一个动点，将直线y=x-2向曲线y=x2-lnx方向平移，直至与曲线y=x2-lnx相切，取切点为P，过点P作直线y=x-2的垂线段，垂足为Q，此时PQ最小，如图所示.

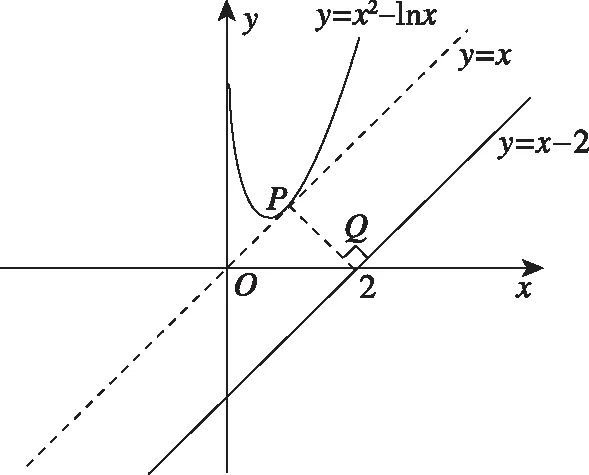
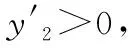
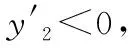
通过上述分析，当x=1时，y2=x2-x-lnx+2取得最小值且最小值为2.

把相机放在支架上，而不是用手拿着，可以得到更干净直接的模糊效果。不妨两种方法都尝试一下，看看你更喜欢哪一种。如果缩小光圈和降低ISO都不能达到足够慢的快门速度，那就装上中灰镜吧。

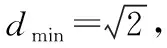
所以m的最大值为2，故选A.

【例3】在直角坐标平面内,与点A(1,2)的距离为1,且与点B(3,1)的距离为2的直线共有( )条.

A.1 B.2

C.3 D.4

思路分析：本题若直接求解,将无从下手,若将数的问题辅以形的意义,就能利用圆的定义画出分别以A(1,2)，B(3,1)为圆心，以1，2为半径的两个圆,然后再根据两圆的位置关系,把问题转化为求两圆的公切线的条数.

因为两圆圆心距

所以圆A与圆B相交,所以公切线有2条.

所以符合题意的直线共有2条,故选B.

评注：本题若直接求解比较困难，但若观数思形，将数的问题辅以形的意义，就有事半功倍的效果，其实这样的方法在高考题中屡见不鲜，要引起高度重视.

【例4】竖立在地面上的两根旗杆的高分别为10米和15米，相距20米，则地面上到两根旗杆顶点的仰角相等的点P的轨迹是

( )

A.圆 B.椭圆 C.双曲线 D.抛物线

思路分析：要求动点P的轨迹,由于P点在地面上,因而只要将动点P所受的空间限制条件转化为动点P在平面上的限制条件,再由相关知识即可求出.

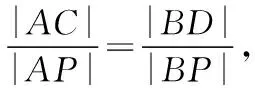
三、精题集萃

1.已知函数f(x)=2lnx和直线l:2x-y+6=0，若点P是函数f(x)图象上的一点，则点P到直线l的距离的最小值为________.

四、总结反思

数形结合思想是我们平时做题时最常用的思想方法之一，数的抽象可以通过形的直观来理解，数形结合就是实现代数与几何之间的相互转化，具体应用表现在以下两个方面：

1.通过坐标系、图象等，“形”题“数”解

借助于直角坐标系可以将图形问题代数化，这一方法在解析几何和立体几何中体现的相当充分.常与以下内容联系：①实数与数轴上点的对应关系；②函数与图象的对应关系；③曲线与方程的对应关系；④以几何元素和几何条件为背景，建立起来的概念，如向量、三角函数等；⑤以函数图象为载体，解决有关函数最值问题等.

2.通过转化构造，“数”题“形”解

在解题过程中，有许多代数结构有着明显的几何意义，因此，可以将“数”与“形”进行巧妙地转化灵活解题，如本文所举的例题.另外，函数的图象也是实现数形结合的有效工具之一，函数思想和数形结合思想经常结合起来应用于解题.

五、高考预测

从目前高考“注重通法，淡化特技，培养素养”的命题原则来看，高考对数形结合的考查主要体现下面三个方面：

一是利用数形结合直观、简捷地解答选择题、填空题.

二是利用数形结合求解解答题，特别是向量法、坐标法在立体几何、解析几何中的应用及函数图象在函数与导数综合问题中的应用.

三是以图表为载体，考查读图、识图及信息转换能力.这种问题在选择、填空题中有增加题量的趋势.

数形结合思想，其实质是将抽象的数学语言与直观的图象结合起来，关键是代数问题与图象之间的相互转化，它可以使代数问题几何化、几何问题代数化.

六、参考答案