“新高考”新题型例说
湖南 欧阳才学
2020年北京、天津、山东和海南的数学高考使用新高考全国卷,“新高考”全国卷将更加注重对“创新意识”的考查.通过创新问题,考查考生对新颖信息、情景设问,选择有效的方法和手段分析信息,综合与灵活地运用所学的数学知识、思想和方法,进行独立地思考、探索和研究,提出解决问题的思路,创造性地解决问题的能力.下面例析几道立意新颖、表述脱俗、背景鲜活和设问独特的新题型,供参考.
一、多项选择题
突出一个主题,设计多个正确选项供考生选择,这是多项选择题主要的呈现方式.教育部考试中心任子朝说:“多选题的引入有利于提高全卷得分率,有利于区分学生,但选项数量设置有必要进行改进.这一题型一般是每题设置4个选项,全部选对满分,选对但不全的得一半分,有选错的得0分.”

( )
A.-3 B.-2



例2.(原创)下面的结论中,正确的是
( )
A.若a,b∈R,则a2+3>2a
B.若a,b∈R,则a2+b2>2(a-b-1)
C.若a,b,c,d∈R,且满足(a2+b2)d2+b2+c2≤2b(a+c)d,则b2=ac
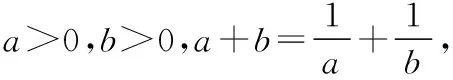
解析:因为a2+3-2a=(a-1)2+2>0,所以A正确;
因为a2+b2-2(a-b-1)=(a-1)2+(b-1)2≥0,所以B错误;
将(a2+b2)d2+b2+c2≤2b(a+c)d变形并整理,得(ad-b)2+(bd-c)2≤0,因此ad-b=bd-c=0,所以b2=ac,所以C正确;
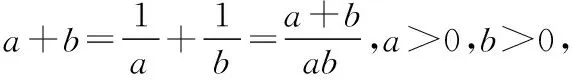
故选ACD.
点评:本题以等式和不等式性质的应用为着手点,综合考查两个实数的大小比较、非负数的性质和基本不等式的应用等知识,以及作差法、配方法、不等化等、“1”的代换等方法技巧,是一道命题(结论)判断的试题.
二、阅读理解题
阅读理解题通过给出一个新概念,或定义一种新运算,或给出新的问题情境,要求在读懂题目的基础上,将新旧知识相联系,剖开现象看本质,实现新信息向已学的知识和方法迁移,达到创新解题的目的.这类问题既能考查学生的阅读理解能力和数学语言转换能力,又能考查学生的探究能力.
例3.已知a,b∈Z,m∈N*,若a和b被m除所得的余数相同,则称a和b对模m同余,记为a≡b(modm).若函数f(x)=2x3-2x2-5x在点x=2处的切线的斜率为a,且a≡b(mod 10),则b的值可以是
( )
A.2 015 B.2 017
C.2 019 D.2 021
解析:因为函数f(x)=2x3-2x2-5x,所以f′(x)=6x2-4x-5,所以f′(2)=6×22-4×2-5=11,所以a被10除所得的余数为1.因为a≡b(mod 10),所以b被10除所得的余数为1.当b=2 021时,b被10除所得的余数为1,故选D.
点评:本题给出“a和b对模m同余”新概念和对应的“新符号”,关键是对新符号“a≡b(mod 10)”的认识和理解.在此基础上利用导数的几何意义求出a的值,再结合选项确定符合新概念的b的值.
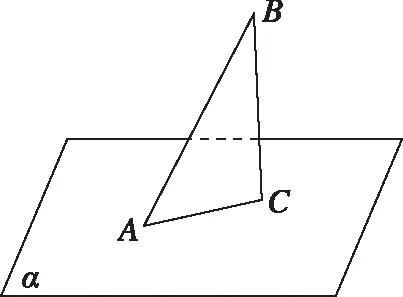
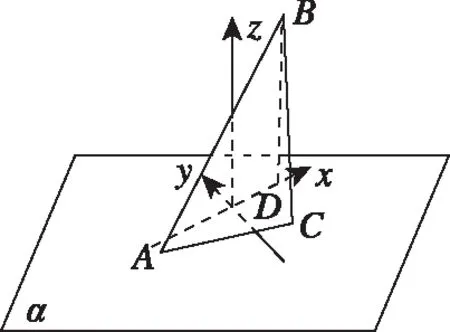
例4.数列{an}中,对任意给定的正整数n,存在不相等的正整数i,j(i (Ⅰ)若仅有3项的数列1,a,b具有性质P,求a+b的值; (Ⅲ)正项数列{bn}是公比不为1的等比数列.若数列{bn}具有性质P,则数列{bn}至少有多少项?请说明理由. ∴a+b=2或a+b=-2. (Ⅲ)设正项等比数列{bn}的公比为q,q>0且q≠1,则bn=b1·qn-1. ∵j>i≥1,且i,j∈N*,∴i+j-2≥1. 这时对于n=1,2,…,7,都存在bn=bibj,其中i ∴数列{bn}至少有7项. 点评:本题以数列知识为载体,以阅读理解能力与推理论证能力为立意,以探索求解为目的,需要考生在理解数列{an}具有“性质P”含义的基础上,将其转化运用到具体的求值、证明及探索等问题情境中,经过运算求解或推理论证,从而解决问题.本题所传递的导向信息很明确,那就是不以“刷题”为备考方式,不以解决高精尖的难题为唯一追求,把复习备考的着眼点放在数学的“问题本质”和能力培养上,将本质性的东西弄熟吃透了,阅读理解、抽象概括及推理论证能力提高了,相应的问题便会迎刃而解. 在知识网络的交叉点处设计试题,是基础性与综合性的最佳表现形式.“新高考”命题注定不囿于单一的知识点,而是从学科知识的内在联系出发,在知识交叉上做文章,注重知识之间的交汇、渗透和整合.一个题目往往包含多个知识点,解题时不能只局限于一个知识点,必须将相关知识纳入一个系统中去考虑,灵活地从一个知识点转到另一个知识点. 例5.如图,AB是平面α的斜线段,A为斜足,点C满足sin∠CAB=λsin∠CBA(λ>0),且在平面α内运动,则 ( ) A.当λ=1时,点C的轨迹是抛物线 B.当λ=1时,点C的轨迹是一条直线 C.当λ=2时,点C的轨迹是椭圆 D.当λ=2时,点C的轨迹是双曲线 当λ=1时,BC=AC,过AB的中点作线段AB的垂面β,则点C在平面α与平面β的交线上,即点C的轨迹是一条直线,所以A错误; 点评:以立体图形为载体,以空间想象能力为立意,设置满足一定条件的动点,着力将动点运动的轨迹设计为直线、圆、圆锥曲线或圆锥曲线的一部分,这是设计立体几何与解析几何交融的创新型试题的常用渠道,对促进思维能力和对核心概念的理解大有裨益,能很好地考查直观想象核心素养和知识的综合运用能力.本题将角的正弦关系转化为棱长的比值后,根据选项中λ的取值分别分析、判断和进一步求解. 整理,得tan2an+1-tan2an=1, 所以数列{tan2an}是以3为首项,1为公差的等差数列, 点评:三角函数、数列与导数是高中课程中极其重要的内容,它们“联姻”设计出的交汇性试题,既能体现数列的基础性,又能体现三角函数与导数的工具作用.本题中的数列和导数都是“幌子”,重在考查三角恒等变换的运用能力. 给出实际应用背景,对研究对象获取相关数据,运用统计方法对数据进行整理、分析和推断,得出结论,从而解决问题. 例7.已知某种细菌的适宜生长温度为10℃~25℃,为了研究该种细菌的繁殖数量y(单位:个)随温度x(单位:℃)的变化规律,收集数据如下: 温度x/℃12141618202224繁殖数量y/个2025332751112194 对数据进行初步处理后,得到了一些统计量的值,如下表所示: xyk∑7i=1(xi-x)2∑7i=1(ki-k)2∑7i=1(xi-x)(yi-y)∑7i=1(xi-x)(ki-k)18663.81124.31 42820.5 (Ⅰ)请绘出y关于x的散点图,并根据散点图判断y=bx+a与y=cedx哪一个更适合作为该种细菌的繁殖数量y关于温度x的回归方程类型(给出判断即可,不必说明理由); (Ⅱ)根据(Ⅰ)的判断结果及表格数据,建立y关于x的回归方程(结果精确到0.1); (Ⅲ)当温度为25℃时,该种细菌的繁殖数量的预报值为多少? 参考数据:e5.5≈245. 解析:(Ⅰ)由题意,y关于x的散点图如图所示, 所以y=cedx更适合作为y关于x的回归方程. 所以y关于x的回归方程为y=e0.2x+0.5. (Ⅲ)由(Ⅱ)中的回归方程可知,令x=25,求得y=e5.5≈245, 所以当温度为25℃时,预报值为245. 点评:本题主要考查数据的散点图的应用,回归方程的求解及应用,合理利用散点图作出判断,准确利用公式求解是解答的关键,着重考查数据处理能力与运算求解能力.本题充分体现了“将数据准备阶段的步骤减少,给考生呈现比较规范的数据格式或数据的回归模型.”把考查的重点后移到对数据的分析、理解、找规律,减少复杂的运算,突出对数学思想方法的理解和运用能力的考查,引导学生从“解题”到“解决问题”能力的培养. 给出一些数据、图形、表格等多种形式的背景材料,通过提供设计条件或结论开放、解题方法多样、答案不唯一的试题,增强试题的开放性和探究性,引导学生打破常规进行思考,通过尝试类比或猜测作出独立的判断,创造性地提出解决方案. 阅读材料:我国著名数学家华罗庚先生曾说:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休.”在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征.我们来看一个应用函数的特征研究对应图象形状的例子. 解析:图象特征: 点评:在研究这样的问题中,我们既用到了从特殊到一般的思想,又用到了分类讨论的思想,既进行了静态(特殊点)的研究,又进行了动态(趋势性)的思考.让我们享受数学研究的过程,传播数学研究的成果.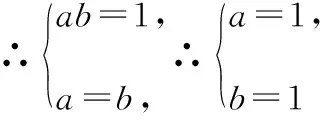
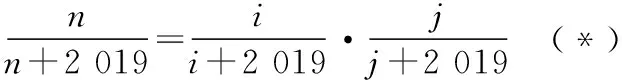




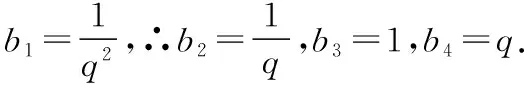


三、知识交叉题



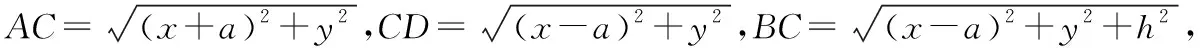
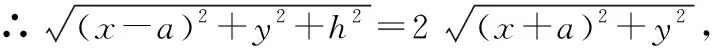


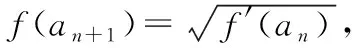

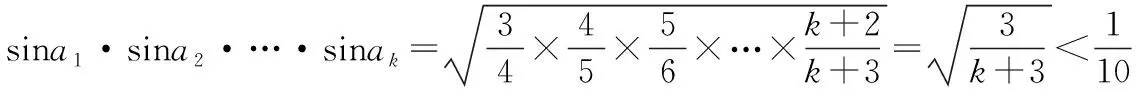
四、数据分析题


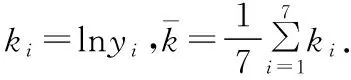



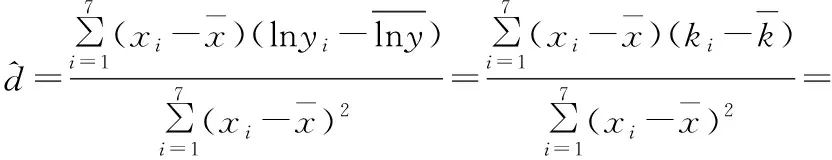

五、材料背景题