函数对称性及其应用举例
安徽 陈晓明
函数是中学数学教学的主线,也是高考重点考查的内容.函数的性质很多,其中函数的对称性问题是一个难点,此类试题经常出现在平时的考试中,甚至在高考舞台也占有一席之地.函数的对称性分为一个函数的自对称性和两个函数的对称性,对称性包括轴对称和中心对称.限于篇幅,这里只给出部分定理的证明,其余定理的证明读者不难完成.
1 一个函数的自对称性
(1)轴对称
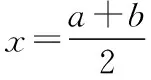
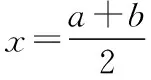
说明(1)特别地,当a=b时,函数y=f(x)的定义域为R,且满足条件f(a+x)=f(a-x),则函数y=f(x)的图象关于直线x=a对称.当a=b=0时,函数y=f(x)的定义域为R,且满足条件f(x)=f(-x),则函数y=f(x)的图象关于直线x=0(即y轴)对称,此时函数y=f(x)为偶函数.
(2)定理的逆命题也成立,即函数y=f(x)的定义域为R,它的图象关于直线x=a对称,则f(a+x)=f(a-x).
(3)f(a+x)=f(a-x)⟺f(x)=f(2a-x).
(4)有对称性(对称轴x=a,对称中心(a,b))的一个或两个函数的定义域只需关于x=a对称即可,不一定就是R.下面情况相同.
(2)中心对称

说明(1)特别地,当a=b时,函数y=f(x)的定义域为R,且满足条件f(a+x)=-f(a-x),则函数y=f(x)的图象关于点(a,0)对称.当a=b=0时,函数y=f(x)的定义域为R,且满足条件f(x)=-f(-x),则函数y=f(x)的图象关于点(0,0)(即原点)对称,此时函数y=f(x)为奇函数.
(2)定理的逆命题也成立,即函数y=f(x)的定义域为R,它的图象关于点(a,0)对称,则f(a+x)=-f(a-x).
(3)f(a+x)=-f(a-x)⟺f(x)=-f(2a-x).
(4)可推广:设函数y=f(x)的定义域为R,且满足条件f(x)+f(2a-x)=2b,则函数y=f(x)的图象关于点(a,b)对称.逆命题也成立.
2 两个函数的对称性
(1)轴对称
定理3设函数y=f(x)的定义域为R,则函数y=f(x)与函数y=f(2a-x)的图象关于直线x=a对称.

说明(1)特别地,当a=0时,设函数y=f(x)的定义域为R,则函数y=f(x)与函数y=f(-x)的图象关于直线x=0(即y轴)对称.
(2)同理可得:设函数y=f(x)的定义域为R,则函数y=f(x)与函数y=2b-f(x)的图象关于直线y=b对称.
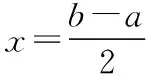
(2)中心对称
定理4设函数y=f(x)的定义域为R,则函数y=f(x)与函数y=-f(2a-x)的图象关于点(a,0)对称.
说明(1)特别地,当a=0时,设函数y=f(x)的定义域为R,则函数y=f(x)与函数y=-f(-x)的图象关于点(0,0)(即原点)对称.

(3)定理4可推广为:设函数y=f(x)的定义域为R,则函数y=f(x)与函数y=2b-f(2a-x)的图象关于点(a,b)对称.逆命题也成立.
3 应用举例
例1(2018·全国卷Ⅱ理·11)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=
( )
A.-50 B.0
C.2 D.50
解析因为函数f(x)是在(-∞,+∞)上的奇函数,所以f(-x)=-f(x),且f(0)=0.因为f(1-x)=f(1+x),所以f(x)的图象关于直线x=1对称,由定理1说明(3)知f(x)=f(2-x),故f(-x)=f(2+x),所以f(2+x)=-f(x),故f(4+x)=-f(2+x)=f(x),所以f(x)是周期函数,且一个周期为4,故f(4)=f(0)=0,f(2)=f(1+1)=f(1-1)=f(0)=0,f(3)=f(1+2)=f(1-2)=-f(1)=-2,所以f(1)+f(2)+f(3)+…+f(50)=12[f(1)+f(2)+f(3)+f(4)]+f(1)+f(2)=2,故本题正确答案是C.
评注由解析不难推广得到:若函数f(x)的图象有一个对称中心(a,0),一条对称轴为直线x=b,且a≠b,则4|b-a|是函数f(x)的周期.



例3设函数y=f(x)定义在实数集R上,则函数y=f(x-1)与y=f(1-x)的图象关于
( )
A.直线y=0对称 B.直线x=0对称
C.直线y=1对称 D.直线x=1对称

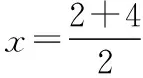

( )
A.1 B.2
C.3 D.4
结束语
高考复习备考中,笔者认为做题、讲题不在多,应当多花点儿精力研究知识点中隐藏的规律性的东西,注重对题型的归纳和总结,在看到个性的同时找到共性.把一类题型做熟练、分析透彻,才能触类旁通,从而培养学生的能力,提高解题效率,提升学生数学核心素养.高考数学复习归根结底还是要落实数学核心素养的提升.

