例析圆与向量的交汇问题
2020-11-04 06:52江苏省宜兴市和桥高级中学214211
中学数学研究(江西) 2020年10期
江苏省宜兴市和桥高级中学 (214211) 王 蓬
近年来经常出现圆与平面向量交汇的问题,这是两个难点的叠加题,由于涉及知识点比较多,给解题增加了难度.本文通过分类举例,并对典型例题进行剖析、对解法进行评注.
一、抓住圆的知识解向量问题

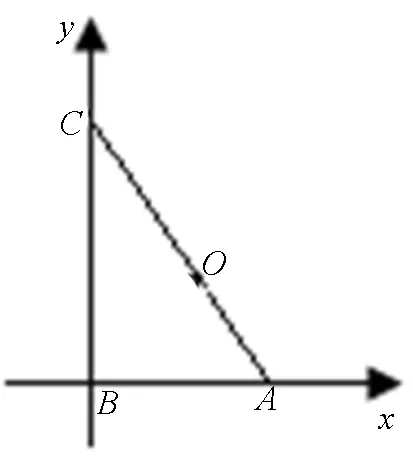
图1
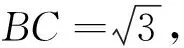
评注:在充分考察已知条件后,将所给三角形特殊化为直角三角形,为后面利用建立坐标系解题提供了便利,这是特殊化解题的一个成功例证,虽然此法不一定是最好,但这是一个重要的解题思路.


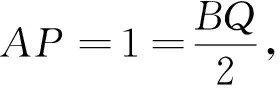
评注:题中的A、B两点分别在两个圆上运动,将两个动向量转化为定向量(长度、方向确定)是解题主要任务,通过建立适当的坐标系、利用函数与方程是解决此类问题有效途径之一.
二、关于圆弧上动点的向量问题
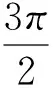
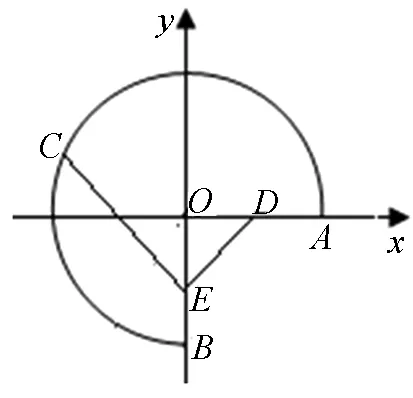
图2
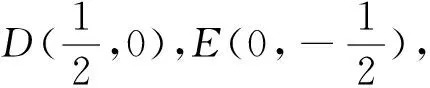
评注:关于圆弧上动点问题,首先需要确定圆心,然后建立以圆心为原点的直角坐标系后,圆上的动点坐标就可以表示出来了,为下面用坐标表示向量后解题扫清了障碍.

图3


评注:题设中的圆弧虽然没有直角,但只要抓住圆心和半径就可以建立直角坐标系,把圆上的动点设出来,这样向量就就能由坐标表示了,同时要注意所设的角参数θ的范围.
三、挖掘隐含圆解向量问题
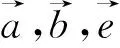

图4
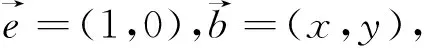
评注:本题中没有点坐标,而是抓住单位向量设坐标,引出了直角坐标系,再通过设动点,根据已知条件得到动点的轨迹为圆,求出圆的方程后再运用圆心到直线的距离解决了问题,其中得到圆的方程并加以运用是解题核心.
例6 已知A,B,C,D四点共面,BC=2,AB2+
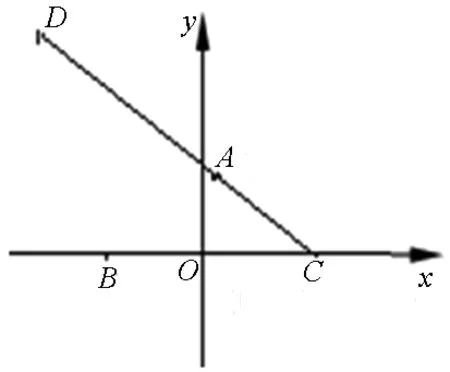
图5
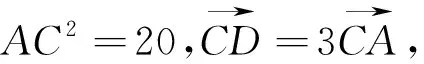



四、运用圆的性质解向量问题
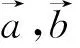



评注:通过建立直角坐标系,设点,就可以把题设条件转化为一个圆的方程,然后利用圆的相关性质使问题化解,题目中虽然没有圆的条件,将已知条件转化变形可以达到目的.
猜你喜欢
北京航空航天大学学报(2022年5期)2022-06-06
建材发展导向(2022年4期)2022-03-16
中学生数理化(高中版.高考数学)(2021年6期)2021-07-28
甘肃教育(2020年14期)2020-09-11
武汉工程大学学报(2019年6期)2020-01-03
中学数学杂志(初中版)(2019年4期)2019-09-18
初中生世界·九年级(2019年6期)2019-08-15
学苑创造·B版(2019年4期)2019-05-09
学苑创造·C版(2018年6期)2018-09-03
知识文库(2018年7期)2018-05-14

