涉及二面角的外接球问题的探究及应用
2020-11-04 06:46福建省泉州市第七中学362000林志敏赖呈杰
中学数学研究(江西) 2020年10期
福建省泉州市第七中学 (362000) 林志敏 赖呈杰
空间几何体的外接球问题一直是各类考试命题的考查热点,时常出现在选择、填空题的压轴题位置,特别是结合二面角知识的时候,学生时常望而生畏,这类考题常以空间几何体为载体,以考查空间想象能力和化归思想为目标,其思维量很大,运算要求较高,需要把空间问题转化为平面问题求解,笔者在研究中发现这类外接球的考题有共同点,可以借助以下结论转化命题,从而轻松解决.
一、几个结论
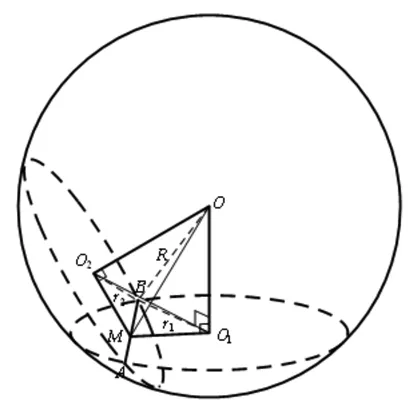
图1





推论3 当α⊥β且AB为⊙O1的直径时,有O=O2,R=r2.
二、一组几何体外接球试题
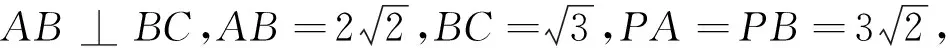
A.100πB.108πC.110πD.111π




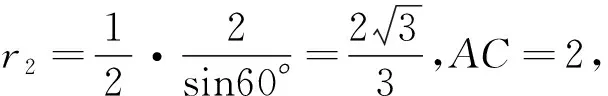


以上几个例题表明对于含二面角的几何体外接球问题,掌握以上模型,对解决该类问题可以做到思路自然,目标明确,而且利用这些结论解题简便易行.
猜你喜欢
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26
作文大王·笑话大王(2022年2期)2022-03-03
新世纪智能(数学备考)(2021年4期)2021-08-06
中学生数理化(高中版.高考数学)(2021年6期)2021-07-28
中学生数理化(高中版.高考理化)(2021年5期)2021-07-16
中学生数理化(高中版.高二数学)(2020年6期)2020-07-24
中学生数理化(高中版.高考数学)(2020年3期)2020-05-25
高中生·天天向上(2018年3期)2018-04-14
高中生·天天向上(2018年1期)2018-04-14

