一道常见作图题的探究

江苏省扬州市甘泉小学 (225123) 赵元翔

一、发现问题，提出猜想

在区里的一节复习公开课上，老师提出:如何在一个长20厘米，宽15厘米的长方形中画一个最大的半圆?结论是：当宽大于或等于长的一半时，以长为直径画出的半圆是长方形中最大的半圆.像这样画最大半圆的作图题经常出现在各式各样的练习中，许多老师对此深信不疑.可是，如果我们带着探究的眼光重新思考这个问题，那么会不会存在一条更长的直径？

二、灵活调整，尝试验证

在长方形中，当宽正好是长的一半时，以长为直径的半圆确实是最大的.但是当宽大于长的一半时，给人感觉是还有“伸展”空间.

首先我们会想到以对角线为直径的半圆(图1)，显然超出了长方形内部.

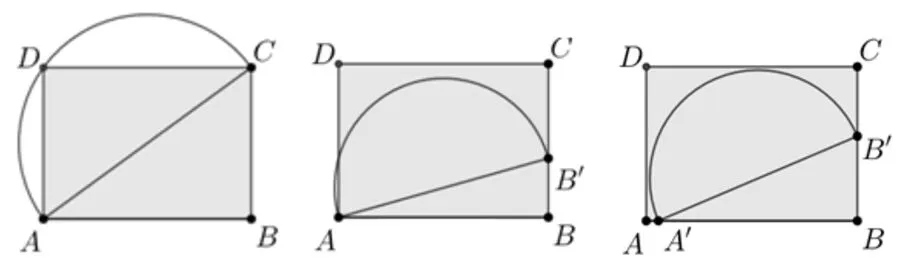
图1 图2 图3

调整1：如图2，将点B向上移动得到点B′，斜边AB′同样大于长AB，但是半圆和线段AD相交，不完全在长方形的内部.

调整2：如图3，如果将点A向右移动，让出一些距离得到点A′，以A′B′为直径的半圆是可以在长方形内部的，并且如果B′C固定，AA′越短，则A′B′越长；AA′固定，B′C越短，同样A′B′会越长.

按照上面的分析，我们可以进行一些初步的尝试，准备一个长20厘米，宽15厘米的长方形纸片和一个直径21厘米的半圆纸片，通过摆一摆、放一放，不难发现半圆是可以完全置于长方形内部的.

三、深入思考，得出结论

笔者经过进一步研究发现了一个优美、统一的数学结论：

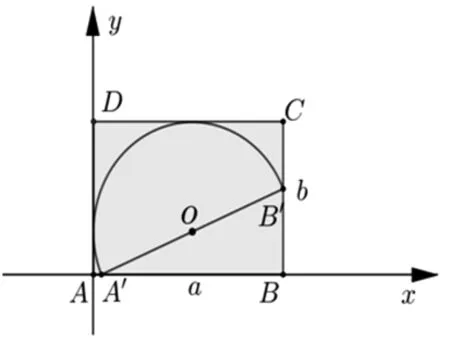
图4

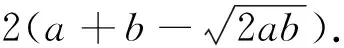
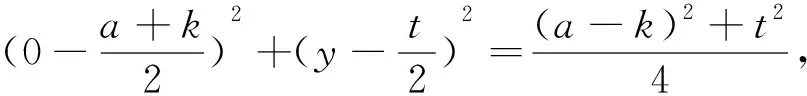
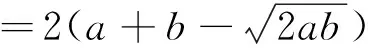
四、回顾反思，经验升华

当a=20cm,b=15cm时，最大半圆的直径为

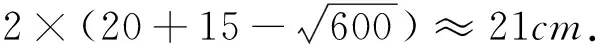
中学老师时常提到小学教错了，工作几年以来，笔者也一直在思考“如何才能教对数学课”，这个“对”不仅指知识本身的对与错，同样也指教学行为的对与错.为什么许多学生从小就觉得数学困难？为什么班上智力好的同学也缺少刻苦钻研的精神？我想不在于学生的“学”，更多的是在于教师的“教”.教师应带着批判的眼光去思考教学观念、去分析教学内容、去研究教学方法，通过强化自身的批判精神唤醒学生数学学习的兴趣和敢于挑战的创新精神.