怎样画长方形里的最大半圆

□陈仲琼

在长方形里画一个最大的半圆，可以采用以下教学过程。

一、当长方形中“长=宽×2”时的画法

1.教师出示题目：请在一个长为4㎝，宽为2㎝的长方形中画一个最大的半圆。学生先独自思考，再画出半圆（如图1）。

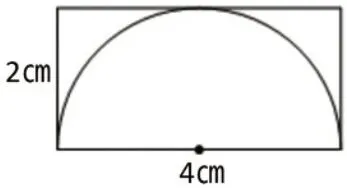
图1

2.教师提问：怎么确定你画的半圆是最大的？学生通过交流讨论，明白半圆与长方形的三条边都碰到了，半圆的半径=宽=长。不可能再长了。

二、当长方形中“长＞宽×2”时的画法

1.教师出示题目：请在一个长为5㎝，宽为2㎝的长方形中画一个最大的半圆。让学生先独自思考，再画出半圆，如图2。

图2

2.教师追问：怎么确定你画的半圆是最大的？学生在操作中尝试寻找更大的半圆，在探索过程中明白，半圆的半径=宽。

三、当长方形中“长＜宽×2”时的画法

1.教师出示题目：请在一个长为8㎝，宽为5㎝的长方形中画一个最大的半圆。学生先独自思考，再画出半圆（如图3）。

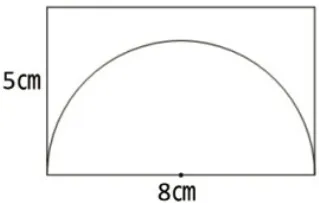
图3

2.教师提问：怎么确定你画的半圆是最大的？学生通过思考，得出结论：半圆的弧顶部没有与长碰到，虽然剩余面积比较大，但左右两边弧都已经与宽碰到，半圆的半径=长。

3.教师追问：确定吗？还能找到更大的半圆吗？启发学生讨论，半圆的大小与半径有关，半径、直径越大半圆越大。让学生尝试操作增大直径，根据“斜边大于任意一条直角边”的性质，画出一条斜边作为直径的半圆（如图4）。

图4

4.教师提示：失败的问题出在哪里？有办法解决这个问题吗？组织学生继续讨论，既然半圆右边的弧画出长方形的边线了，就将直径右边缩进来一点，可以解决吗？学生尝试画图调整，在操作中有感悟，但很难画出标准半圆，不确定这种半圆是否会更大。因此，在学生尝试后，教师借助几何画板演示，让学生直观地理解这个半圆更大（如图5）。这类特殊情况超过六年级学生的知识经验，只需要直观感受即可。

图5

四、延伸总结类型

教师呈现图1、图2、图3和图5，引导学生观察这三种情况。教师提问：你发现了什么？师生共同小结。当长方形的“长≥宽×2”时，最大半圆是正的，半径=宽；当长方形的“长＜宽×2”时，最大半圆是斜的，直径＞长。