他山之石 借以攻玉——第14届国际数学教育大会“数学与创造力”专场综述

□张学峰 罗艺文

创造力是指产生新思想，发现和创造新事物的能力。在人类科技迅猛发展的今天，知识的累积速度在飞速增长，对于当代儿童来说，仅仅学习固有的知识，已经远远不能应对未来的挑战，创造力成为21世纪的社会对人才提出的新要求。《义务教育数学课程标准（2011年版）》《义务教育数学课程标准（2022年版）》都将创造力作为重要的培养目标之一。但教学中如何落实创造力的培养一直是困扰教育工作者的难题。

在第14届国际数学教育大会上，来自不同国家和地区的研究者在“数学和创造力”（ICME-59）小组（以下简称ICME-59小组）中分享了与创造力相关的最新研究成果。他山之石，借以攻玉，笔者试图以ICME-59小组分享的内容为基础，择要分享介绍，供关注创造力研究的教育工作者参考借鉴。

一、创造力的特征与评价

在世界发展日新月异的今天，创造力的重要性毋庸置疑。小学数学教学应着力提升学生的创造意识是相关教育工作者的共识。那么到底什么是创造力，如何评判创造力的高低，在我国当前的数学教师群体中却鲜有人深入研究。教师如果不能理解什么是创造力，无法说明怎样才是创造力较高的表现，那么培养创造力自然也就成了一句空话。因此，在谈创造力培养前，先要了解创造力的特征，建立创造力的评价体系格外重要。

（一）创造力的特征

在不同的时期学者们关于什么是创造力有不同的界定。心理学家吉尔福德（Guilford）认为，创造力是指那些具有杰出创造表现的人们所具有的能力。［1］盖哲尔（Getzele）认为创造力可以是一个独一无二或意想不到的成果，可以是个体参与的一种非算法的决策过程，也可以是一种以各种方式来分析问题从而辨别模式、发现相似性和差异的能力［2］。哈达玛（Hadamard）总结出创造力的四阶段发展模式：准备（完全理解问题），沉思（在头脑中有意识地自动解决问题），启迪（在沉思过后产生内在想法），验证（确定该想法是否正确）。［3］虽然人们对创造力的理解各不相同，但多数学者常以“产生新思想，发现和创造新事物的能力”或“能够创造出新奇有价值的产品的能力”来界定创造力［4］。在ICME-59小组交流与汇报中，大家关于创造力的研究与分析，均建立在以上共识的基础上展开。

（二）创造力的评价

关于创造力评价的相关内容，在ICME-59小组交流中得到广泛的关注。其中，多数相关评价均以“托伦斯创造性思维测试”为基础展开。“托伦斯创造性思维测试”指的是用“流畅性”“灵活性或变通性”“独创性或新颖性”“精致性”等因素，对解决问题中体现出的创造力高低进行评价的一种方式。［5］流畅性指的是可以想出很多可能性或答案的能力。灵活性或变通性指的是能以不同观点来做不同的分类或不同的思考，从某种思维灵活转换到另一种思维的能力。独创性或新颖性指的是创造独特的作品，或体现出不寻常的思维的能力。精致性指的是制订详尽计划或概括想法的能力，也就是在问题解决时，从最初的构想或观念逐步发展，让自己的构想逐步完美或形成新观念的能力。

这些因素中，流畅性、灵活性和独创性三个因素常常在中小学阶段创造力研究中被广泛使用，以确定学生在数学问题解决方面的创造力水平。如南京师范大学金海月在《对中国高中生探究与创新意识的探索》的研究中，结合“托伦斯创造性思维测试”设计相关问卷展开调查。浙江外国语学院教学月刊社邢佳立和香港教育大学张侨平、金轩竹（以下简称“邢佳立等”）在《通过数学活动题培养学生创造力的实践探索》的报告中，以“托伦斯创造性思维测试”为基础，根据研究内容与学生实际，从灵活性、掌握度和原创性等方面对学生在问题解决活动中的创造力进行评价。

特别值得关注的是与此不同的两位学者的研究。

其一是来自北京师范大学的王艳芝在《小学生数学创新能力评价体系的建立：基于德尔菲法的调查与分析》的报告中，介绍了一套自己开发的培养和评价学生数学创新能力的标准和工具（如表1）。这套标准是作者结合相关研究，并向来自高校和科研机构的19位专家进行了三轮意见征询后，形成的评价创造力的5个一级指标和13个二级指标。

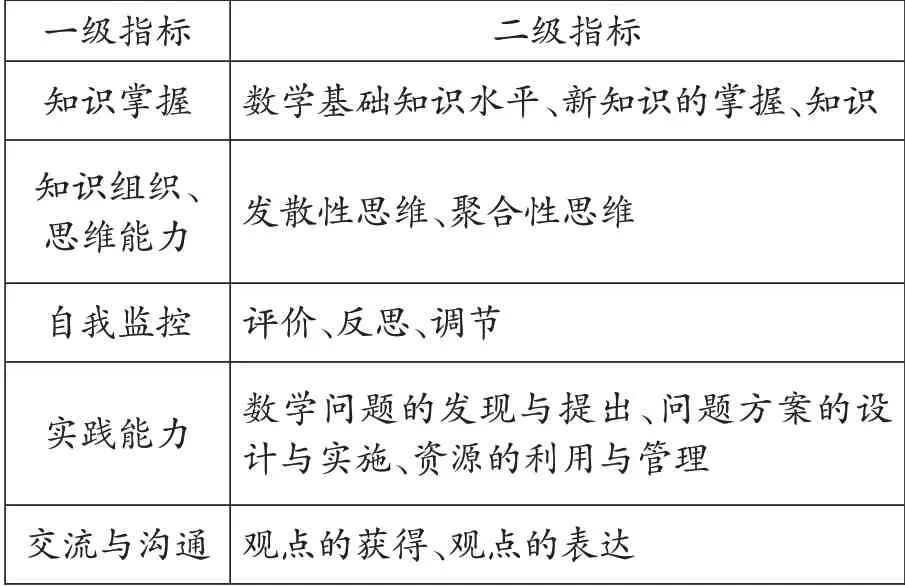
表1

其二是以色列的Haim Elgrably,Roza Leikin分享了《谈与策略相关和结果相关的数学创造力：普通学生与资优学生的比较》的实验报告，他的研究虽同样以“托伦斯创造性思维测试”为基础，但他进一步提出了“在比较大众与资优者的创造力时，相对创造力与绝对创造力间的对比是核心”这一重要观点，并将创造力区分为“策略相关的创造力”与“结果相关的创造力”。他通过研究得出：资优人士数学创造力的主要特征是与策略有关的高度灵活性和与结果有关的原创性。

以上内容为我国学者进一步研究创造力的评价指明了方向：“流畅性”“灵活性或变通性”“独创性或新颖性”“精致性”等因素是评价创造力高低的重要依据，在具体评价时可根据自身的研究对此工具适当进行调整。同时，创造力评价工具的开发还有极大的研究空间。

二、有关创造力的调查

在数学教育中，数学创造力研究主要关注的是创造性的问题解决。在ICME-59小组交流中有多位学者介绍了关于“创造力”水平及影响因素的调查结果。

(1) 高温后方钢管再生混凝土柱的主要破坏过程和破坏形态与常温试件相似，均表现为试件根部(加劲肋顶部)钢管鼓曲破坏，侧面也有明显的鼓曲波形，如图4所示。

德国的Daniela Assmus,Torsten Fritzlar认为数学资优儿童可能具有特殊的创造力。他们进行了“拓展小学生成长模式——一项激发创造力的任务”的对比实验案例研究，对14名有数学天赋的儿童和29名普通儿童进行了个案调查，分析发现：①有数学天赋的三年级学生的成长模式比普通学生的成长模式更丰富、更稳定；②资优儿童的类型具有多样性。

德国的Anastasia,leftheriou和塞浦路斯的Nektaria Panagi-Louka,Athanasios Gagatsis围绕小学几何的空间能力与创造力间的关系，对来自塞浦路斯和希腊的192名五、六年级学生展开调查。他们围绕创造力的流畅性、灵活性和原创性特征，通过给学生布置有关面积和周长的多解法任务，了解学生的创造力。研究结果表明，在问题解决的过程中，学生表现出的流畅性和灵活性具有强烈的一致性，总是共同出现，而原创性极少在学生中被观察到。

菲律宾的Lady Angela Mico Rocena,Ma.Nympha B.Joaquin,日本的Manabu Sumida,Naomichi Yoshimira在《菲律宾和日本学生的数学创造力》的比较研究报告中，介绍了对来自菲律宾和日本的两组共140名学生的问卷调查结果。该问卷经过了内容验证、试点测试（先导测试）和可靠性测试，而后运用统计测试分析结果。他们通过深入研究学生对有关数字和数感开放式问题的回答，探讨了菲律宾和日本学生的数学创造力特征，结合课堂观察并分析了相关文档，如教师制作的评估和教科书，以证实统计结果。结果显示，两组学生的数学创造力有明显差异，日本学生的得分更高，而这或许与教学内容、教学方式有较大关系。

德国的Svenja Bruhn，对10名一年级学生在两个开放性算术任务中，表现出的个人创造力进行观察，发现10个学生中有7个学生的个人创造力在完成不同任务时表现不同，也就是说个人创造力在完成不同任务时存在差异。

美国的Irina Lyublinskaya,Marta Cadral的研究很有特点，他们在《深化初中数学教师几何思维的艺术创造过程》的报告中，重点介绍了他们尝试对“将数学和艺术的创造性结合起来，以加深中学教师对难以教授的几何概念的理解，并改善他们有关这些课题的教学”进行研究的过程。他们的研究表明，创造力对思维有着至关重要的作用。艺术为数学教师提供了能体现更高创造性的参与方式，可以帮助教师以不同且更富创造性的方法欣赏和理解教学规律及数学内容。

南非的Motshidisi Gertrude van Wyk进行了“南非小学数学教师对数学资优学生的看法调查”，研究者调查并分析了基础教育阶段，教师在满足资优儿童学习需求方面的准备情况。通过问卷调查和结构性访谈，研究者分别向Thaba Nchu地区选定的10所小学的教师和校长收集了数据。结果显示：由于缺乏资优教育方面的教师培训，资优学习者的学习需求在常规课堂中难以得到满足；64%的教师有能力教授资优学生；88%的教师认为高等教育机构需要在其课程中加入资优教育的相关内容；70%的校长鼓励教师参加与培养资优生相关的研讨会，以满足资优生的学习需要。

以上调查样本数量差异较大，研究的方向各异，但所有调查的过程翔实，对数据的处理分析清晰可信。这些调查不仅有助于一线教师了解目前国际上创造力研究的相关成果，也可以成为一线教师进行实证研究的范例。

三、有关如何培养创造力的研究

（一）开放性、探究性学习任务有利于创造力培养

多位学者的研究表明：数学学习中的开放性、探究性学习任务有助于学生的创造力培养。

邢佳立等的研究中介绍，在解决开放性的活动题时，学生是知识的积极建构者而不是被动接受者。解决这类问题，学生会经历“识别—探究—操作—反思—验证”等过程，在每一个环节中都能体现创造力的不同水平（如图1）。

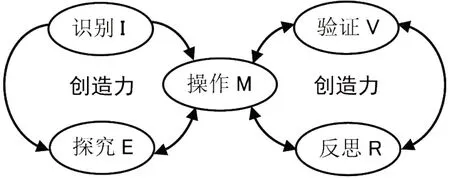
图1

挪威的Hanna Zdziarska Slabikowska的“数学课堂上的探究性对话与数学表征，与其在数学学习中的作用”的研究同样发现，基于探究的数学对话、推理和数学表征之间的联系有助于学生理解数学概念。

北马其顿的Valentina Gogovska的“提高数学创造力的操作性活动”的研究指出，文字任务、魔方、数学谜语和图形字谜可以作为激励和鼓励学生对数学感兴趣的工具。在这些工具的帮助下，学生完成开放性任务可以提高对数学和数学谜题的兴趣，加深对知识的理解，发展创造力，这些活动还有助于学生自主建立知识结构，形成长期记忆。他们在实验中还发现，指出问题和讨论解决方案不仅可以提高学生的创造力，还可以提升学生的数学思维。如果在开放性活动中鼓励学生思考制定新任务，他们会提出更多不同的解决问题的方案。经常进行开放性活动的学生在处理新问题时常常比别人想得更多、更远。

德国的Torsten Fritzlar,Karin Richter在《用数学“重新思考世界”》的报告中，介绍了以包豪斯的几何棋作为创造数学思想和材料的基础，让小学生和师范生在“包豪斯象棋（如图2）项目”活动中完成“对世界的再思考”过程，展示了包豪斯象棋如何帮助学生实现创造性活动。

图2

日本的Noriko Tanaka在《研究问题和学生评估》的报告中指出，学生在自己编制和研究问题的过程中，可以提高对数学的兴趣，激发创造力，并体会到数学的用处。研究者通过实际例子的分享，介绍了这种方法在课堂内外两种不同的背景下的应用，并展示了学生分享研究的过程，以及在口头会议（报告）和书面会议（报告）上相互评估的情况。

（二）合作式学习方式有助于创造力培养

合作式学习方式有助于创造力培养也是多位研究者的共识之一。几乎所有相关调查分析都提及合作对学生的创造力培养具有重要作用。同时，ICME-59小组介绍的与合作相关的研究不仅局限于学生，也包括成人之间的合作。

智利的Alicia Venegas-Thayer在“数学专业与音乐专业大学生之间的合作性创作”的研究中，组建了一个由数学专业和音乐专业的学生共同组成的小组，通过随机实验进行音乐创作。研究者在两个专业学生的互动中观察到，音乐—数学创作程序的建立取决于每个参与者的专业实践，他们常常对照自己学科的典型常规，谈论另一学科的研究对象。这样的跨学科项目能给不同学科领域的人提供协同合作的机会，并有助于创造力的产生。

希腊的Dimitris Diamantidis在“数学教师的合作，数字化教学工具的创意设计”的研究中，让参与实验的希腊数学教师在真实的学校环境中共同合作，以希腊教育部在网上提供的正式版电子教科书为初始工具，重新设计数学教学的数字化工具，并在课堂上使用，然后根据使用情况再设计、再修改。他们以Strauss和Corbin的基础理论范式为分析依据，发现这样的合作有助于教师个体创造力的展现，教师团体内的合作与交流等特点也在合作中得以显现。

（三）社会层面的参与有助于创造力培养

俄罗斯的Mariia Pavlova,Maria Shabanova在题为《学生为娱乐科学博物馆制作“实验数学”互动展览》的报告中提出，参观娱乐性科学博物馆是普及科学知识和科学活动的趣味形式之一，在这样的博物馆里，因为每个人都可以触摸展品并进行实验，所以展品具有极强的可互动性。研究者希望能让学生有机会自己创造一个展览，并介绍他们实现这一想法的过程——来自大学和中学的学生为阿尔汉格尔斯克的一个娱乐科学博物馆制作综合的“实验数学”互动展览。参与研究的学生体现出了很强的创造力，在完成任务后他们表示，希望教师从“实验科学”这个新的、不寻常的角度来介绍数学，告诉他们实验在数学发现中的作用，并让他们觉得自己是真正的研究者和实验数学家。

希腊的Chronis Kynigos,Dimitris Diamantidis进行了“建构主义课堂背景下的社会创造力”的研究，他们认为：社会创造力是从集体中的“个人”与计算媒体、技术、人工制品之间的交互中生长出来的，同时，社会创造力也为个人开展工作提供了帮助；个人创造力是“社会文化”资产的来源和表现；社会创造力也发生在除“社会”背景外的“技术”背景中。这项研究，将学生创造性想法的产生视为社会技术环境中的正常产出。研究也表明，在这种环境里教师发挥了重要作用，教师应鼓励学生创造性地提出问题和解决问题。

创造力至关重要，以数学课程培养学生的创造力，在近年来已成为数学教育的重要目标，为数学教育工作者所关注，但有关创造力的研究在我国尚处萌芽阶段。期待以上针对“数学与创造力”国际研究进展的梳理，能为我国关注创造力的研究者提供参考，从而促进我国学生创造力的提升。