一道高考题的推广

上海市七宝中学 (201101) 吴祖丰

(浙江省2019年数学高考第21题) 过焦点F(1,0)的直线与抛物线y2=2px(p>0)交于A,B两点，点C在抛物线上，△ABC的重心G在x轴上，直线AC交x轴于点Q(点Q在点F点右侧)．

图1

(1)求抛物线的方程及准线方程；

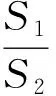
一、试题解答

本题考查了抛物线的几何性质是圆锥曲线中的“非对称性问题”，主要涉及圆锥曲线中设点、设直线的切入问题，其最大难点在于三角形面积的表示以及复杂的函数运算以及最值求解.可以设直线、设点、也可以通过面积比值化简后再进行最值运算，但三种方法没有大的本质区别，最终都是殊途同归通过函数求出面积比的最值.

分析：通过常规的设直线来表示三个点之间的关系，进而用斜率m表示出面积比.由于本题面积比是一个非对称性问题，因此用m表示时相对较为繁琐，化简计算需要一定的时间，具体解法如下.

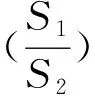
二、试题拓展

对于圆锥曲线问题，常常可以把一种曲线的性质推广到其他曲线，本题亦可作如下拓展：

1.变定曲线为任意抛物线

评注：将固定抛物线改为任意抛物线，其它条件不变，此时求得重心坐标为则为G(p,0).

2.变定点为任意点

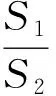
评注：在变式1的基础上把定点变为数轴正半轴上的任一点，发现结论与定点的位置并无关系.

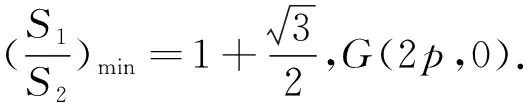
3.变抛物线为椭圆

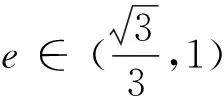
4.变定点变曲线

评注：在变式3的基础上再进一步加强条件，定点变成了椭圆长轴上的非焦点，此时要取到面积比的最值需要保证定点的范围.

三、问题本质探究

继续深入探究可以发现，问题的本质其实与抛物线或椭圆并无关系，同样也可以将本题结论延拓到双曲线，或者直接把问题从圆锥曲线中剥离出来.下面运用向量工具证明该模型中的最值结论.

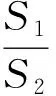
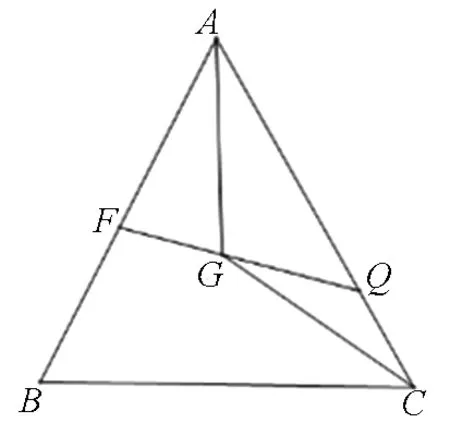
图2

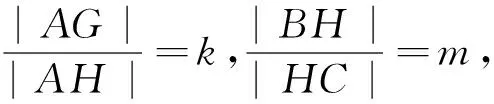
四、总结反思

从上述探究不难发现，本题的模型可以从抛物线上三点推广到椭圆或双曲线上三点，也可以拓展到任意三点，直接“架空”曲线.从这个角度来讲，本题失去了圆锥曲线解析的本质，但确实给人以耳目一新的感觉，或许这样是试题已经很难用“难或简单”加以评论，因为它本身就是在考查学生的综合素养.那么，如何在有限的时间里，实现“透过表象看本质”？相信只要在平时的教学过程中注重对问题本质的探究，注重学生发散性思维的培养，注重学生核心素养的提升，那么还是有可能快速破解此类问题的，或者至少会进行多角度尝试并简化运算.