解析几何中的五种定值问题再厘清*——《“翻”出课堂，“转”出精彩》研究之系列

湖北省大冶一中 (435000) 陈志刚

解析几何中的定值问题是近几年高考命题的一个热点和难点．在求解过程中要根据题目特点，制定适当的解题方案，配合代数运算，才能达到解题目的．在教学中若能提高解决此类问题的效率，对学生思维的深度，做题的专注度，以及基本运算能力的培养，都有非常积极的意义．

一、线段长为定值

首先设法将要求的线段或与相关的线段通过设点、设直线(斜率)表示出来，再抓住点在曲线上进行一些代数变形可达到解题目标．

图1

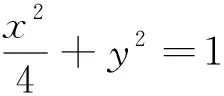
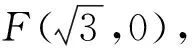
评注：本题所求的线段是定点到动直线的距离，而动直线又是定圆与动圆的交线，下面只要通过设椭圆一动点建立动圆的方程就解决线段表示的问题了，所以建立动圆方程是问题解决的核心．

二、斜率为定值

直线的斜率与点的坐标有关，如何通过设坐标表示出要求的斜率很重要，多数时候是先求点，再求表示出斜率．

评注：本题中所求斜率的直线是椭圆的弦所确定的直线，所以利用解决椭圆的弦所在的直线方程的方法是非常有效的解题途径．解题过程中抓住角平分线的特点分别设出直线PA、AQ的斜率是成功解题关键．

三、面积为定值

这类题中的面积大部分是三角形或四边形面积，充分利用某边与坐标轴或定直线垂直，可以降低列式和解题的难度．

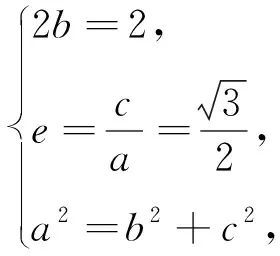
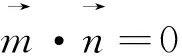
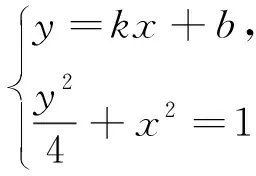
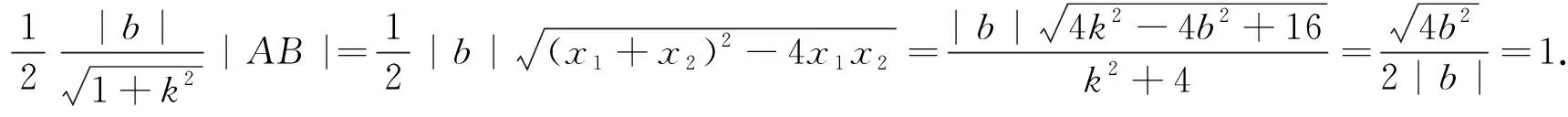
评注：如何表示出椭圆的内接三角形的面积是解题的关键，如果已知一条边与坐标轴垂直，用坐标差就可以表示，如果没有此条件，只能用点到直线的距离和和弦长来解决．

四、数量积为定值

解析几何中的向量问题，大多都是采用设点解决的，所设的点要尽量用已知的量表示出来，这样就能降低后面的计算难度．

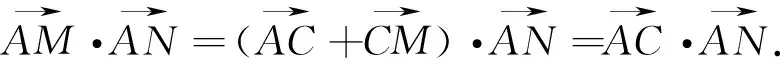
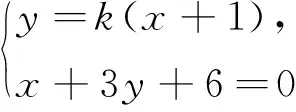
评注：题中的向量比较多，首先是找点将其表示出来．通过将动直线方程与已知方程联立得到动点N的坐标是关键，但必须注意动直线l与x轴垂直与否，不确定时需分类讨论．

五、关系式为定值

所谓的关系式大多与线段、坐标有关，利用题设条件先将此关系式用参数表示出来，然后再设法消去参数解题．

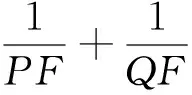
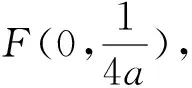
点评：本题是抛物线问题，相对容易，设法用坐标表示出关系式是解题的核心，又因为与曲线的弦有关的，将直线方程与曲线方程联立，通过消元，运用根与系数的关系解题是非常重要且实用的解题方法．