直线与抛物线关系中的两个推广结论
福建省德化第三中学 (362500) 庄明丽
直线与抛物线的交点问题、位置关系是高考的重要考点,考查方式多样化,如定点、定值、相切、范围等等,这类问题的解答通常都具有通性通法,不外乎利用方程思想结合一元二次方程根与系数的关系加以解决,但是往往运算量较大,很多学生不一定能得出最终的结果.若是能利用一些二级结论在解题(尤其是选填题)中加以运用,势必能达到事半功倍的效果.本文从一道引例的解答中获得灵感,深入探究并拓展与推广,最终获得两个实用的一般性结论供借鉴与应用.

(1)求点C的轨迹方程;
(2)经过点F(1,0)的动直线l与点C的轨迹方程交于A,B两点,在x轴上是否存在定点P(异于点F),使得x轴为∠APB的角平分线?若存在,求出P的坐标;若不存在,请说明理由.

思考:第二步的结论即在x轴上存在点P(-1,0)使得x轴为∠APB的角平分线即kPA+kPB=0,而kOP=0即kPA+kPB=0=kOP.我们把本题第二小步的结论记为结论1,即:
结论1 过抛物线y2=4x焦点F(1,0)的直线l与抛物线交于A,B两点.已知P(-1,0),连接PA,PB,则kPA+kPB=kOP.
点P(-1,0)刚好与焦点F(1,0)的横坐标互为相反数,这是巧合还是具有一般性呢?点P(-1,0)刚好是抛物线y2=4x的准线与x轴的交点,如果是准线上的其他点是否也满足kPA+kPB=kOP呢?经过探究发现,结论1可以做以下推广:
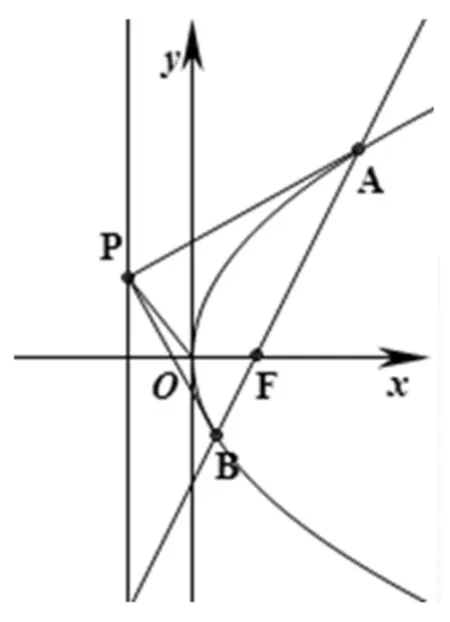
图1
推广1 如图1,过抛物线y2=2px(p>0)焦点F的直线l与抛物线交于A,B两点.已知点P为准线上的点,连接PA,PB,则kPA+kPB=kOP.


查阅这几年高考,2018年全国卷Ⅲ的填空题第16题的立意与此类似,原题如下:
已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°则k=2.
本题可以用常规方法解答,还可以用推广1的结论:设直线AM,BM的斜率分别为k1,k2,根据已知条件和推广1有k1·k2=-1,k1+k2=kOM=-1,从而可求得k1,k2,便可以得到直线AM或者BM的方程,也就不难求出A或者B点坐标,那么问题也就解决了.
推广1中直线l过焦点F,且点P的横坐标跟焦点F的横坐标互为相反数,如果直线l不是过焦点而是过定点x轴上的其他定点,且点P所在直线方程为此定点的横坐标的相反数,对应的结论会不会成立呢?

图2
推广2 如图2,过点C(n,0)(n>0)的直线l与抛物线y2=2px(p>0)交于A,B两点,点P所在直线的方程为x=-n,连接PA,PB,则kPA+kPB=kOP.
证明:设直线l的方程为x=ty+n,联立

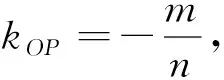
2018年全国卷Ⅰ的文科试题就考过这样的一道题,立意与推广2类似,题目如下:
设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.
(1)当l与x轴垂直时,求直线BM的方程;
(2)证明:∠ABM=∠ABN.
简证第二步:由推广2的结论知kBM+kBN=kBO=0,即BN,BM斜率互为相反数,故∠ABM=∠ABN.
从推广2的证明过程中可以发现这个结论跟n>0没有关系,所以推广2还可以再推广:
推广3 如图3,过点C(n,0)(n<0)的直线l与抛物线y2=2px(p>0)交于A,B两点,点P所在直线的方程为x=-n,连接PA,PB,则kPA+kPB=kOP.

图3
证明过程与推广2一样,这里就不重复了.从推广2和3看出,不管直线所过定点在x轴的正半轴还是负半轴,都会有kPA+kPB=kOP.如果抛物线开口向左,那么结论同样成立.焦点在x轴成立,那焦点在y轴会不会也有这样的结论呢?用同样的方式探究发现这结论kPA+kPB=kOP并不成立.焦点在y轴的抛物线方程变为x2=2py(p>0),再结合推广2的证明过程,不难看出焦点在y轴时的结论只要把那些斜率倒数一下就可以了.
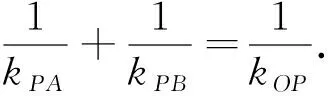

图4

开口向下的也同样有此结论.
因此抛物线具有这样的性质:
(1)过定点C(n,0)(n≠0)的直线l与抛物线y2=±2px(p>0)交于A,B两点,点P所在直线的方程为x=-n,连接PA,PB,则kPA+kPB=kOP.
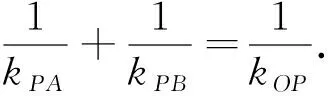
由此可见,学习数学知识若是经常性地做一些探究、推广、归纳、总结,长此以往,可以激发和提高我们的发散思维能力和创新思维能力.抛物线中还有很多类似的结论等着我们去发现.比如上面2018年全国卷Ⅲ的填空题第16题的原题如下:
已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与c交于A,B两点.若∠AMB=90°,则k=2.


