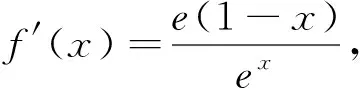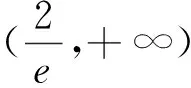基于“怎样解题表”的数学教学设计
——以一道函数综合题为例
南京航空航天大学苏州附属中学 (215000) 吴双民
一、问题提出
《普通高中数学课程标准(2017年)》指出:教师要努力提升教学设计和实施能力,把握数学知识的本质、理解其中的教育价值,把握教学中的难点,理解学生认知的特征;在此基础上,探索通过什么样的途径能够引发学生思考,让学生在掌握知识技能的同时,感悟知识的本质,实现教育价值.,在数学教学过程中,学生不可避免地会碰到一些难以下手的题目,或是对概念理解不透彻,或是题目本身难度较大,学生对题意理解困难较大,这时候教师应该在充分理解知识本质的同时,根据学生的实际情况,设计符合学生认知规律的教学方案,从学生的思维起点出发,在学生困惑处重点讲解,并及时反思小结,理清知识之间的关联,使学生能够融会贯通,掌握知识的本质.
著名数学教育家G.波利亚在《怎样解题》中提出解题的四个步骤:理解题目;拟定方案;执行方案;反思.“理解题目”是弄清楚题目中的已经条件有哪些,要解决什么问题;“拟定方案”是寻找解题思路,找出已知数据和未知量之间的联系,是关键步骤;“执行方案”是将之前的解题思路付诸实践;“回顾”是检查已经得到的解答,反思还有不同的方法吗?能在别的题目中利用这个结果或者方法吗?为了有效引导学生掌握解题的正确方法,笔者引用波利亚的“怎样解题表”,以一道函数综合题为例,探索合理的教学设计,深入剖析解题思路,启发学生思考,培养学生的思维能力.
二、试题分析

(1)求f(x)的极值;(2)若在区间(0,e]上,对于任意的x0,总存在两个不同的x1,x2,使得g(x1)=g(x2)=f(x0),求a的取值范围.
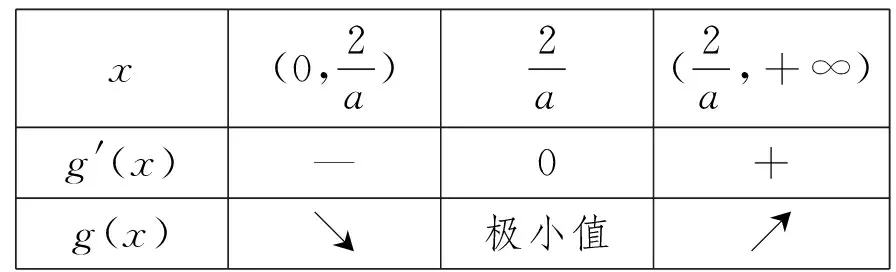
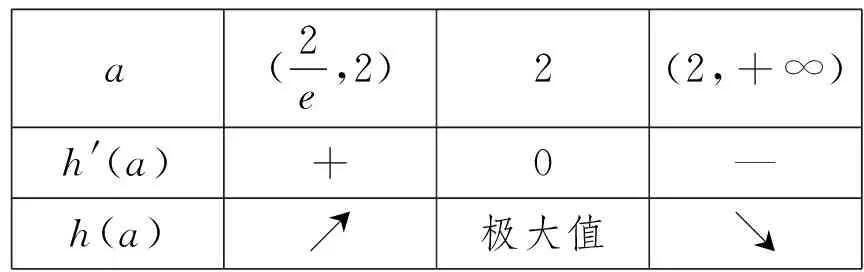
该题目来自2016年徐州三模卷,涉及到的知识点是导数在研究函数中的应用,函数与方程,均为B级要求.本题已知条件给定两个函数,其中f(x)是已知函数,g(x)中的参数a是未知函数.第一小问求f(x)的极值,是常规题,考察利用导数研究函数的极值;第二小问考察g(x)的图象,方程g(x)=f(x0)有两个不同的解,转化为直线y=k,(0 1.理解题目 在这一步要弄清楚题目的已知条件是什么,需要解决的问题是什么,已经条件和未知结论之间有哪些联系. 要解决的问题:对于任意的x0,总存在两个不同的x1,x2,使得g(x1)=g(x2)=f(x0),求a的取值范围. 根据函数f(x)的表达式和定义域[0,e]可以得到函数f(x)的性质,如单调性,值域,图象等,对任意的x0∈(0,e],f(x0)的值来自于函数的值域,它不是一个定值,而是在某个范围内的值.总存在两个不同的x1,x2,使得g(x1)=g(x2)=f(x0),是指g(x)=f(x0)有两个不同的解,如何确定这个方程有两个不同的解?问题可以转化为函数y=g(x)的图象与直线y=f(x0)有两个不同的交点. 2.拟定方案 这个阶段的关键是找出已知条件与未知量直接的联系,可以类比迁移已经解决的相似问题,你能否想到一道更容易着手的相关题目?本题的难点在于第二问的题意学生理解起来有困难,这句话“任意的x0,总存在两个不同的x1,x2,使得g(x1)=g(x2)=f(x0)”需要分解难度,为帮助学生理解题意,设置两个引例. 引例1若方程f(x)=k有两个不同的解,求k的取值范围. 引例1与问题:“若存在两个不同的x1,x2使得f(x1)=f(x2)=k,求k的取值范围.”有何不同?问题的本质是一样的,只是呈现的形式不一样,引例1的目的是将难点分解,梳理方程的解的个数问题的一般处理思路,将方程f(x)=k有两个不同的解转化为函数f(x)的图像与直线y=k有两个不同的交点,进而将问题转化为研究函数f(x)的图像.这个题型是学生熟悉并能解决的题型,给学生铺设台阶,从熟悉的问题出发,通过转化与化归将不熟悉的问题转化为熟悉的问题,将题中的f(x0)用k来代替,直线y=k是动直线,函数f(x)的图像是确定的,问题就是一个定的函数图像与动直线的交点问题,学生更容易接受和理解. 在问题解决的过程中,通过引例一复习回顾方程解的问题与函数图象的交点的转化,通过引例二函数与定直线有两个交点问题过渡到题目中一组平行直线系与函数有两个交点,层层铺垫,将难点分解,学生更容易接受.学生解决了上述两个问题后,大致可以确定本题的解题思路: 3.执行方案 解题方案给出了一个总体的框架,这一步将解题计划付诸实践,写出完整的解题过程,检查解题过程中的每一个细节,确定每一个步骤的正确性和可行性.解答过程如下: x(0,1)1(1,+∞)f'(x)+0-f(x)↗极大值↘ 得f(x)极大=f(1)=1. (2)由(1)知f(x)在(0,1]上递增,在[1,e]上递减,所以对∀x0∈(0,e]有f(x0)∈(0,1],令f(x0)=k,方程g(x)=k,0 x(0,2a)2a(2a,+∞)g'(x)—0+g(x)↘极小值↗ a(2e,2)2(2,+∞)h'(a)+0—h(a)↗极大值↘ 为了进一步检验学生对这一知识点的理解,对数学思想方法的掌握,笔者设置了两道变式拓展,激发学生探究的欲望,点燃学生的学习热情,在探究讨论中体验解题的成就感. 引申1:方程解的问题转化为值域之间的包含关系 引申2:将等量关系转化为不等关系 拓展引申1中改变了问题的呈现方式,引申2将等量关系转化为不等关系,难度进一步增加,培养学生探究问题的意识. 4.回顾三、教学设计