重视基本图形学会转化划归
吴洁慧

摘要:圆在初中平面几何中是非常重要的一块内容,近年来中考中往往和三角形、四边形结合命题,2020年浙江台州数学中考的第23题就是这样一道在圆背景下的几何综合题。本题的解决需要学生具备一定的直观想象、数学建模、逻辑推理、数学运算等核心素养。整理了此题的多种解法,并对试题导向进行了一定的分析。
关键词:基本图形;转化;划归;方程;数学建模
一、试题呈现
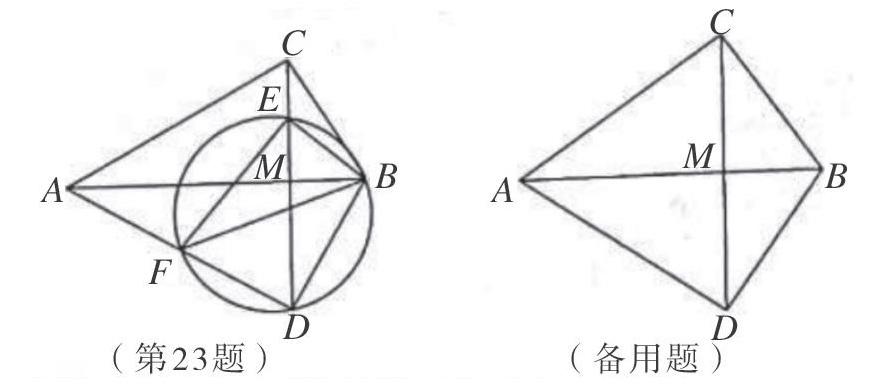
(2020台州中考第23题)如图,在△ABC中,∠ABC=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M,E是线段CM上的点,连接BE,F是△BDE的外接圆与AD的另一个交点,连接EF,BF.
(1)求证:△BEF是直角三角形;
(2)求证:△BEF∽△BCA;
(3)当AB=6,BC=m时,在线段CM上存在点E,使得EF和AB互相平分,求m的值.
二、基于核心素养的试题评价
(一)关注核心内容,全面考查基础
本题以圆为背景,全面考查了初中阶段“图形与几何”的核心内容,特别是三角形的相关内容,这些内容都是初中阶段课标要求的基础知识和基本技能。第(1)题考查了“翻折”—轴对称的性质、直角三角形的判定。第(2)题考查了相似三角形的判定。第(3)题考查了相似三角形的性质与判定、平行四边形(矩形)的性质与判定、勾股定理、垂径定理的应用。特别是“EF和AB互相平分”也就是线段的特殊的数量关系,由此得到直线AF和BE“平行”的特殊的位置关系,再确定动点E的位置,从而确定BC的长度,符合几何从一般到特殊的研究规律。这小题中考查了初中求线段的几种基本方法,特别是利用相似三角形找线段的比例关系、建立方程并求解这种一般路径。这是初中生必须掌握的基本方法和基本技能。
本题的第(2)小题的图形中,有很多学生在平时练习中遇到并总结过的基本图形。题干中的“筝形”来自人教版教材八年级上的全等三角形,圆内接四边形的图来自于九年级上的内容,第(3)小题的线段计算则可以用到“母子相似”“A子字形相似”“X字形相似”“共边共角型相似”等相似三角形的基本图形。這些基本图形,能帮助学生顺利地进行转化划归,将圆背景的综合问题转化到三角形问题去解决,因此此题对学生分析解决问题的能力提出了较高要求。
(二)凸显思想方法,直击核心素养
这是一题圆背景的几何综合题,本题的解决需要学生具备一定的逻辑推理、几何直观、数学运算、数学建模等核心素养,对学生几何的四基和四能有很好的检验和评价作用。特别第(3)小问的求值问题,需要学生在复杂几何图形中发现基本图形,并利用相似三角形的性质或者勾股定理等基本方法建立方程模型求解,综合考查了直观想象和数学建模的素养,也考查了转化划归的数学基本思想方法。同时,由于点 E 是动点,由它的特殊性需要在备用图中画出准确图形,也考查了学生基本课堂活动经验的积累,只有能相对准确画出图形的学生才会发现由EF和AB互相平分可以得到EB∥AD,加上第(1)小题得到的∠BEF是直角,可知四边形EFDB是特殊四边形矩形这个结论,才能根据“射影定理”“勾股定理”等建立方程模型,因此平时的教学我们一定要重视学生的动手画图能力,积累必需的作图经验,要让学生经历知识的发生过程,明确定理使用的条件。
三、部分多解、优解赏析
(一)第(1)题的解法分析
RT△的判定,通常有三种方法:①直接证明一个内角是直角;②证明两锐角互余;③证明三边满足a2+b2=c2,也就是应用勾股定理逆定理。本题题干中没有线段长度的条件,故无法考虑第三种方法。
解法1:因为△ABD是由△ABC翻折而来,故△ABD ≌△ABC,可得∠ABD =∠ABC=90°。又B、E、F、D内接于圆,利用“圆内接四边形对角互补”可得∠BEF=90°。
解法2:得到∠ABD =∠ABC=90°后,利用圆周角推论可得BF是直径,再利用“直径所对圆周角是直角”得到∠BEF=90°。
解法3:得到∠ABD =90°后,将它分成两个角∠FDE和∠BDE,再利用“同弧所对圆周角相等”,将这两个角分别等量代换到∠FBE和∠EFB,得到∠FBE+∠EFB=90°,利用两锐角互余的三角形是直角三角形得证。
简析:显然,运用解法3的同学对教材中圆内接四边形的基本图形不够熟悉,但是能进行正确的等量代换,说明其还是具备了一定的几何素养。
(二)第(2)题的解法分析
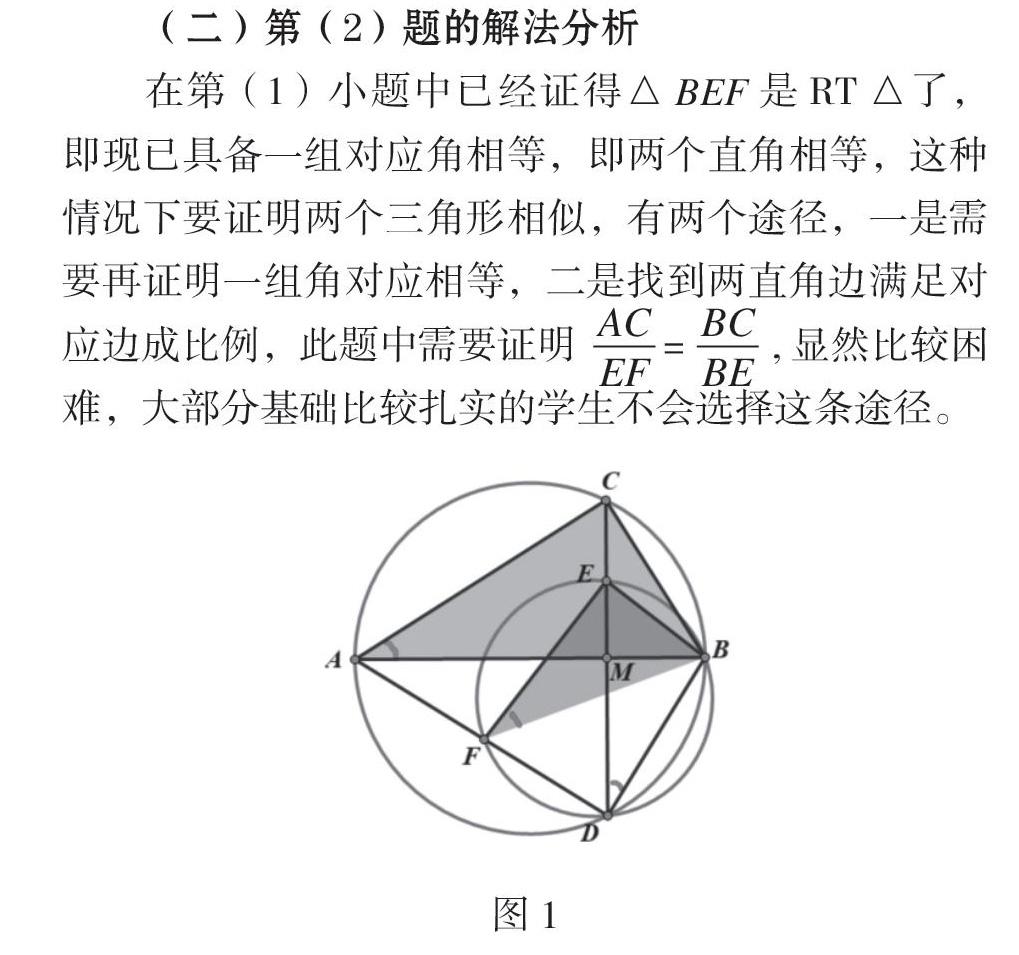
在第(1)小题中已经证得△BEF是RT△了,即现已具备一组对应角相等,即两个直角相等,这种情况下要证明两个三角形相似,有两个途径,一是需要再证明一组角对应相等,二是找到两直角边满足对应边成比例,此题中需要证明 = ,显然比较困难,大部分基础比较扎实的学生不会选择这条途径。
解法1:如图1,由(1)得知∠ABD =∠ABC =90°,可得A、C、B、D四点共圆,故∠CAB =∠CDB(或∠CBA =∠CDA),又B、E、F、D内接于圆,可得∠EFB =∠CDB(或∠EBF = ∠EDF),∴∠CAB=∠EFB(或∠CBA =∠EBF).
解法2:如图2,∠ACB=90°,CD关于AB轴对称,故CD⊥AB,可以发现母子相似的基本图形,利用同角的余角相等,可得∠CAB=∠1,再由轴对称性可得∠1=∠2,又B、E、F、D内接于圆,可得∠EFB =∠2,∴∠CAB=∠EFB。
或者要证∠CBA =∠EBF也是同样的。
简析:解法1用了两次等量代换,显然较为快捷,且学生能使用四点共圆,必定平时的学习是有拓展思维的。解法2用了三次等量代换,次数要多一次,但是用解法2的同学观察到了“母子相似”这一基本图形,这一基本图形可以帮助我们通过“射影定理”得到很多的线段的数量关系,很多的角的数量关系,对第(3)小题的解决会起到一定的作用。
(三)第(3)题的解法分析
这一小题的解法是最多的,但是绕不开建模的思想,也就是根据线段的数量关系建立方程,一般几何中可以找到的等量关系就是相似三角形对应边成比例,以及直角三角形的勾股定理。
1.思路1:相似与勾股结合,利用射影定理或者勾股定理将线段表示成关于m的代数式,最后根据相似三角形对应边成比例或勾股定理建立方程。
几何题中求线段长度最常用的基本方法是根据三种关系列等式:勾股,相似,等积。在本题中显然等积法的计算量过大,不具有优势,但是并非不可以。这个方法虽然繁复,但是可以将几何中计算线段的基本方法在此题的解法中补充完整。其实,此题中有非常多的直角三角形,所以线段之间的数量关系也可以用三角函数去表示;另外,本题的相似和勾股非常多,多种组合均可列出更多方程或方程组,笔者这里就不再一一列举了。
所谓一题多解,多解归一,最终划归为根据数量关系建立方程模型,因此通过此类几何题能够检验出学生的划归能力和建模能力的水平,能够衡量出学生的数学素养。
四、从特殊到一般的试题拓展
此题是EF和AB互相平分,从而得到线段之间特殊的数量关系。如果我们将它一般化:
教师也可将原题中AB的长度改成其他数值,此时,解题思路和方法依旧不变。一则是希望学生能理解研究几何的一般规律:一般到特殊,特殊到一般,以及理解动态问题中的不变的关系和量。另一则也是希望学生能领悟代数问题中的数式通性。
五、教学导向分析与教学建议
杨乐院士在《现代数学发展及其对基础教育的影响》中指出:“平面几何这一人类历史上非常重要的理论,我们还是应该很好地掌握,因为我觉得现在还没有别的东西能代替平面几何对中学生进行几何直观能力和逻辑推导能力的训练。”
而多年来,浙江省内多地虽然采用不同版本教材,但是各地中考均坚持关注核心内容及其教学,关注考查核心素养,类似这样的命题对几何解题教学起到正面积极的导向作用。
本题虽然是圆背景下的几何综合题,但是转化划归后,实际上是需要解决三角形问题,因此在解题教学中,我们一定要引导学生在平时的解题过程中及时归纳总结基本图形,并熟悉基本图形,包括熟悉图形的特征及基本元素之间的位置关系和数量关系。学会在复杂的图形中分离出一些基本图形,将复杂的问题转化为我们熟悉的问题。
要能发挥好“基本图形”的作用,实质上是要帮助学生在研究平面几何的过程中学会思考,提高发现和提出问题、分析和解决问题的能力,这是能力和素养的标志。
而要发挥“基本图形”的力量,解题教学的设计可以先“基本图形”,再“变式图形”,最后“综合图形”,让学生在连续有关联的几何问题解决中得到逻辑推理论证的技能训练,学会灵活运用概念、性质解决平面几何问题。
教师要引导学生明确基本图形的条件和适用情形,在推理过程中必须每一步都论据充分,用归纳、演绎进行推理,避免出现胡乱套用,或者逻辑不清的情况。此外,切忌拿“基本图形”的结论作为定理使用,我们要用严密性、准确性和明确性作为逻辑推理能力的衡量标准。
参考文献:
[1]易良斌.中学数学教与学研究与引领[M].北京:光明日报出版社,2015.
[2]章建跃.数学教育随想录[M].杭州:浙江教育出版社,2017.
[3]章建跃.立体几何教学中的幾个问题[J].中学数学月刊,2015(10).
(责任编辑:奚春皓)

