2020年高考全国Ⅰ卷立体几何试题解析及备考建议

广州市执信中学(510080) 朱清波

2020年高考全国Ⅰ卷对立体几何知识点的考查延续了近几年较为稳定的命题特点,依然分为客观题和主观题两部分,其中理科客观题有3 道,主观题1 道；而对应文科试卷中相关知识点的考查为客观题2 道,主观题1 道,其中2 道客观题与理科同题,只是个别题序有所不同.该特征表明全国卷继续朝新高考文理同卷模式在平稳过渡,试题重点考查考生空间想象能力、推理论证能力以及运算求解能力.但从本次考试评卷反馈结果来看,客观题依旧暴露出考生空间想象能力不足的问题,而主观题求解过程中因为需要涉及大量带根号结构的边长运算,考生运算能力弱导致出现题平均得分比往年降低较多的现象,这一事实需要我们在下一年备考中引起足够的重视和针对性复习.以下就2020年高考试题中立体几何部分试题分析其特点,明确下阶段备考复习方向并提出相关建议.

一、2020年高考Ⅰ卷文理卷立体几何试题解答与评析

题目1(文理科第3 题)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为

解答如图1,设E为CD中点,连接PE.不妨设CD=a,PE=b,则由题意化简得即解得(负根不符题意,舍去),故选C.

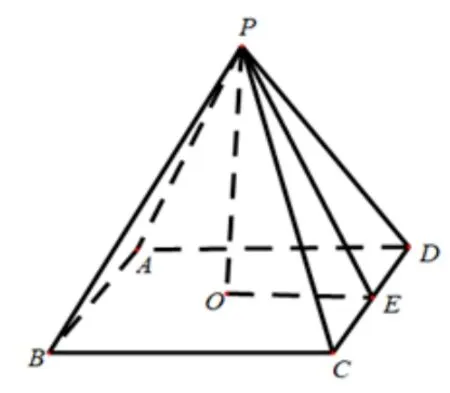
图1

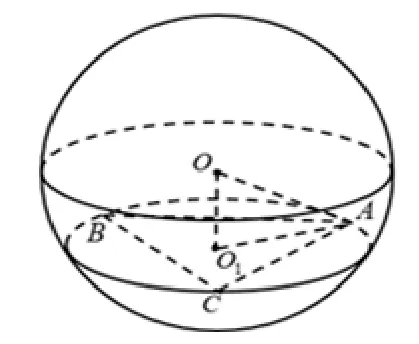
图2

评析本题既渗透了数学文化,又融入了美育教育,题干中的关键词“形状可视为”揭示金字塔的真实形态和数学抽象后的细微差别.题目主要考查正四棱锥相关的概念及其数学运算能力,如棱锥的高以及侧面三角形等基本概念,总体难度不高.

题目2(文科第12 题、理科第10 题)已知A,B,C为球O的球面上的三个点,⊙O1为ΔABC的外接圆,若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为

A.64πB.48πC.36πD.32π

解答如图2,设圆O1半径为r,球O的半径为R,依题意,πr2=4π,解得r=2.又ΔABC为等边三角形,由正弦定理有AB=2rsin 60°=故OO1=平面ABC,则OO1⊥O1A,R=OA=所以球O的表面积S=4πR2=64π,故选A.

评析本题考查球体的表面积公式,需要学生有一定空间想象能力,能根据所给条件粗略画出满足条件的空间图形,当然应用球的截面性质和平面几何中的一些常规结论是正确解出本道题的关键,总体难度中等.

题目3(理科第16 题)如图3,在三棱锥P-ABC的平面展开图中,AC=1,AB=AD=AB⊥AC,AB⊥AD,∠CAE=30°,则cos ∠FCB=____.

图3

解答由题意AB⊥AC,由勾股定理得BC=同理得BD=所以BF=BD=

在ΔACE中,AC=1,AE=AD=∠CAE=30°,由余弦定理得CE2=AC2+AE2-2AC×AEcos 30°=则CF=CE=1,在ΔBCF中,BC=2,BF=CF=1,再由余弦定理得cos ∠FCB=故答案为

评析本题充分体现了高考试题灵活多变的特点,命题形式并没有遵循众多模拟题中空间翻折问题平面化后求值或求最值的套路,而是通过翻折平面化后的结构反向推测原几何体的结构特征,以此考查学生的空间想象能力.这需要考生会利用平面图形翻折回到空间结构过程中的不变量来架设桥梁,再利用各种已知数据解三角形,考查学生计算和数据处理的能力,本题综合性较强,考生有思路但未必能计算准确,从难度上来分析属于中档题.

题目4(文科第19 题) 如图4,D为圆锥的顶点,O是圆锥底面的圆心,ΔABC是底面的内接正三角形,P为DO上一点,∠APC=90°.

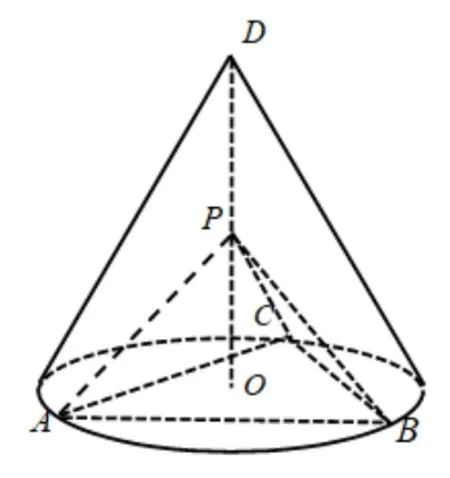
图4

(1)证明：平面PAB⊥平面PAC；

(2)设DO=圆锥的侧面积为求三棱锥P-ABC的体积.

解答第(1) 问的证法1.由题设可知,PA=PB=PC.由于ΔABC是正三角形,故可得ΔPACΔPAB,ΔPACΔPBC.又∠APC=90°,故∠APB=90°,∠BPC=90°.从而PB⊥PA,PB⊥PC,PA ∩PC=P,故PB⊥平面PAC,PB ⊂平面PAB,所以平面PAB⊥平面PAC.

评析该思路即为本题预设的最常规的处理方式,考生经过分析将要证明“面面垂直”的方向调整到先证明“线面垂直”,继而反向去寻找线面垂直中的那条“线”,最后去探究两组线线垂直的思路,而学生利用平面几何的全等条件很容易构建上述思路,当然利用结构的对称性重点证明其中一组就可以了,同理本题通过证明“PC⊥平面PAB”来得到“平面PAC⊥平面PAB”这一结论也是可行的.这也体现了高考立体几何综合题“低起点入口宽”的基本特点.

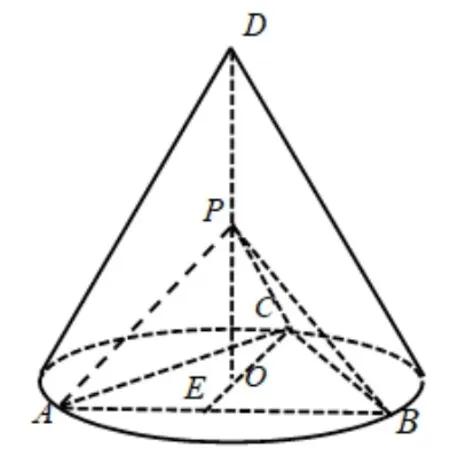
图5

第(1) 问的证法2.如图5,由题设可知,PO⊥平面ABC.所以PO⊥AB,连接CO,延长CO交AB于点E,则CO⊥AB,从而AB⊥面POC,所以AB⊥PC,由于∠APC=90°,则PC⊥PA,所以PC⊥面PAB,而PC ⊂平面PAC,则有面PAC⊥面PAB.

评析该思路另辟蹊径,运用该方式处理的考生很大一个可能是头脑中有一个基本模型所形成的结论：直角四面体的对棱异面垂直(AB⊥PC),有了该结论后再围绕这个点去寻找本题需证结论的其它条件,最后进行思路整合,因此该方法能体现出部分学生的立体几何知识储备和学科基本素养.

第(2) 问的证法1.设圆锥的底面半径为r,母线长为l.由题设可得rl=l2-r2=2.解得r=1,l=从而AB=由(1)可得PA2+PB2=AB2,故PA=PB=PC=所以三棱锥P-ABC的体积为V=×PA×PB×PC=

评析本题第(2)问主要考查锥体体积公式和侧面积公式,根据所给条件假设并解出几个基本量,再结合第一问的相关结论来计算出对应几何体体积,难点在于侧面积公式和体积公式的记忆是否准确,另一个就是考生临场选择三棱锥底面和对应高的灵活性,因此本题得分的特点是极差较大.

第(2) 问的证法2.设⊙O的半径为r,由S侧面积=得r=1,从而AB=注意到在ΔAPO中AP=所以

评析该思路与第一种方法比较而言,主要是选择几何体的底面和高相对更常规,但运算量更大,同时依旧在考查锥体侧面积公式和体积公式的结构,其难点还是在两个公式的记忆是否准确以及考生是否具备较强的计算能力.

题目5(理科第18 题) 如图6,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD,ΔABC是底面内接正三角形,P为DO上一点,

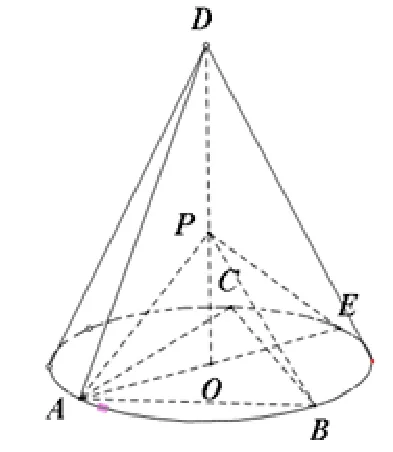
图6

(1)证明：PA⊥平面PBC；

(2)求二面角B-PC-E的余弦值.

解答第(1) 问证法1 (几何法1).设DO=a,由题设可得因此PA2+PB2=AB2,从而PA⊥PB.又PA2+PC2=AC2,故PA⊥PC.而PB ∩PC=P,所以PA⊥平面PBC.

评析本小问考查目标指向较为明确,考生只需要找到两组线线垂直的关系即可,而垂直关系的证明指向很容易将思路转换到求各种长度再利用勾股逆定理检验是否成立,因此对基础边长的设定和相关长度的运算就显得尤为重要,本题的第一问主要是考查逻辑推理,难点在于边长计算的准确性.从评卷反馈来看,无论怎样设定单位长度,部分线段的长度始终带有根号结构,导致运算出错率非常高,而相当多的考生明知计算出来的边长不能形成直角三角形也不作修改,抱着侥幸的心理去书写后续过程,也说明其对运算的信心是严重不足的.

第(1)问证法2(几何法2).如图7,由题意,O是ΔABC的外心,故BC ⊥AO,又PO⊥面ABC,BC ⊂面ABC,则PO ⊥BC,又PO ∩AO=O,故BC⊥面PAO,PA ⊂面PAO,故BC ⊥PA,设AO的延长线交BC于M,则M为BC中点,连接PM,不妨设OA=OB=OC=1,则AD=2,DO=PA=由PA2+PM2=AM2,则PA ⊥PM,而BC ∩PM=M,则PA⊥面PBC.

评析与第一种方法思路不同的是,部分理科考生受到惯性思维的影响,通过日常积累的小结论,容易先发现“利用BC⊥面PAO得到BC⊥PA”这一基本事实,然后找不到其它方向后思路再转换到勾股逆定理方向去证明剩余一组垂直关系,但证明完垂直关系后才发现会有更多的线线垂直方法,总的来说考生用这种思路来处理表明其欠缺一些整体思考,没有梳理好方向就开始答题导致其证明过程走了一些弯路.

图7

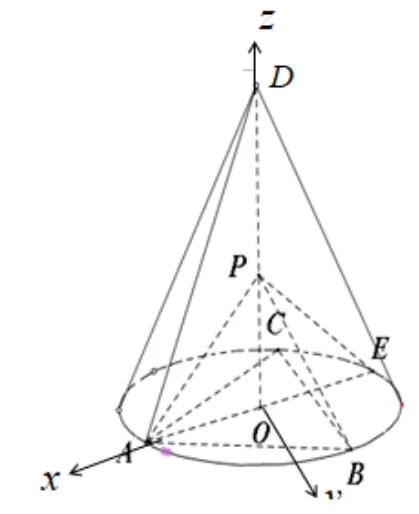
图8

第(1)问证法3(向量法).如图8,以O为坐标原点,以方向为x轴正方向,以方向为z轴正方向,建立直角坐标系.

设AE=AD=a,依题意得所以由=0,所以⊥,同理=0,所以⊥,而PB ∩PC=P,又PA/⊂面PBC,所以PA⊥面PBC.

评析该思路也很自然,因为本题的两问都是研究一个相对较为规则结构的性质,考生自然会想到用建系设坐标来处理整道题,但难点在于基础边长的设定和对应点的坐标需准确无误的写出来,否则后续计算毫无意义；而实际评卷反馈中有大量考生建系方式出错或建系方式与对应坐标数据不一致,用错误的坐标数据得出了部分正确的结论,因此得分并不理想.

第(1) 问证法4 (基底法).设DO=1,则PO=OA=OB=

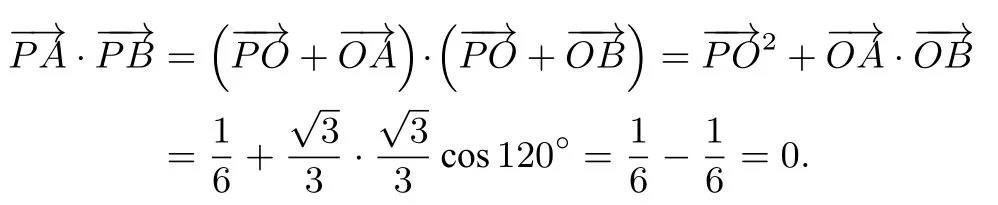
所以,PA⊥PB.同理得PA⊥PC,而PB ∩PC=P,所以PA⊥面PBC.

评析用该方法处理的考生敏锐的捕捉到了该几何体中存在共点的三条棱,夹角明确且棱长均可求,体现了向量作为运算工具的优越性.

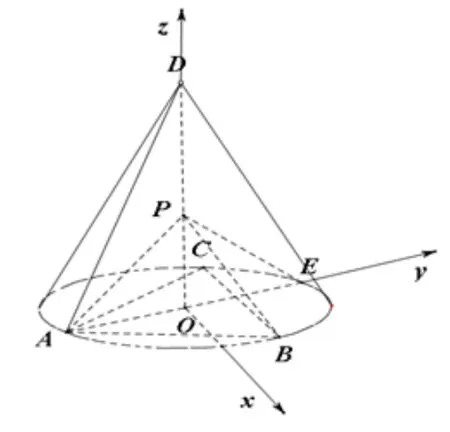
图9

第(2)问解法1.如图9,以O为坐标原点,的方向为y轴的正方向,不妨为单位长,建立如图所示的空间直角坐标系O-xyz.由题设可得E(0,1,0),所以=

设m=(x,y,z) 是平面PCE的法向量,则即

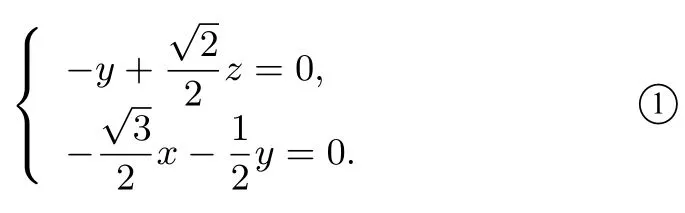
可取

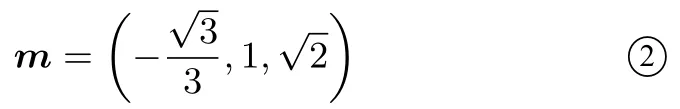
评析本小问较为常规,首先是建系可以选择不同的方位,边长的设定也比较灵活,但部分考生缺乏整体意识,忽略了第一问对第二问的帮助,导致重新去求面的法向量,当然因为坐标中根号结构较多,对学生计算能力有较高的要求,另外考生需明晰法向量的夹角和二面角的平面角的区别,下结论需要严谨.

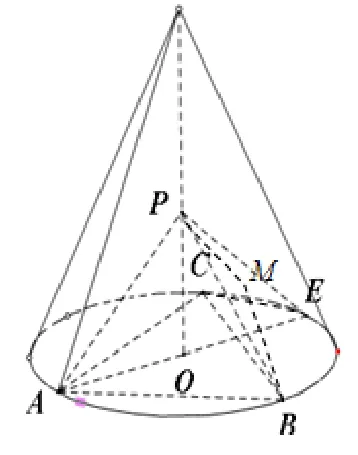
图10

第(2) 问解法2(等体积法).如图10,过B作面PCE的垂线BM,垂足为M,设OA=1,则BC=由PB2+PC2=BC2,所以BP⊥PC,故∠BPM为二面角B-PC-E的平面角,又利用等体积法BM=,sin ∠BPM=则

评析利用等体积法求二面角的平面角,基本模式是“设—证—求”三步骤的模式,对几何体的结构是否方正要求不高,算法结构也比较清晰,但对考生的空间想象能力要求较高,运算量也比较大,与建系运算的方式相比各有优势,因此两种方法都需要灵活掌握.

二、备考复习建议

1 重视立体几何中的基本概念,加强对立体几何中公式和定理的理解

近几年高考关于立体几何的考查都突出了基础性,教材在编写上实际上已经充分考虑到了学生的认知规律,内容安排上体现了由具体到一般,而考点要求从合情推理过渡到逻辑推理.但教师在教学时往往在概念形成上用时较短,把教学重心放在了后续的公理和定理的应用上,而考生在答题时对基本概念认知不清晰和运算所需公式记忆出错是得分不理想的一个重要原因,如本次高考试题中出现的正四棱锥概念、球体的表面积公式以及圆锥的侧面积公式等,均需要考生在备考复习过程中熟练掌握；在评卷过程中,也发现部分学生不确定圆锥顶点在底面上的投影是否为底面内接正三角形的重心,花了较长篇幅去论证这一基本的结论；也有学生在处理理科18 题第一问时用向量的思路去证明线面垂直,但方向却是去证明=0,这表明学生并没有弄清相关原理；还有学生直接通过面面垂直得到线面垂直或线线垂直等错误的推理来论证答题等,上述众多因素导致大题基础得分不乐观,因此在备考复习中一定要重视立体几何章节中各类概念、公式、定理的再回顾.

2 重视立体几何中基本模型和简单基本结论

通过查阅近几年高考对本章内容的考点,不难发现其对基本模型的考查频率是较高的,如正棱柱和正棱锥、球体,圆锥等,而相关几何体结构中的基本结论需要学生在日常复习中要做到了然于胸,如柱体、锥体外接球球心的位置规律、正方体的内嵌正四面体中点与线的位置关系、平面几何中圆的垂径定理类比到空间的相关性质等,通过平时的积累,让考生在临场发挥时能快速准确的找到解题方向.

3 重视运算求解能力的培养,改善“会而不全”的现象

数学运算是学科核心素养之一,也是众多考生在面对立体几何问题最大的挑战,2020年高考理科18 题从评卷反馈来看,因为该几何体结构的基础性和对称性,考生出现了近6种建系方案,加上对基础边长的不同设定,约有12 种不同的坐标数据出现,但其中近半数方案中能正确写出点的坐标难度较大,特别是根号结构的出现频率高,导致考生运算结果大量出错,许多考生答题思路清晰但往往从坐标数据那里出错,会而不全,导致最后只能拿到较低的步骤分,这也是本题得分率低的最主要原因.教师在日常的备考中,要重视示范一些运算常规技巧,如出现了等分点时可以把基础长度设大一些(变成几个量的最小公倍数),法向量的坐标形式尽量回避分数或分式,坐标数据中负号尽量出现的少一些等,另外不要在关键步骤上尝试心算,书写过程的草稿要尽量集中以便于随时检查等,同时提高相关训练的运算强度,做到限时训练,同时教师要改变课堂上重思维不重运算的教学习惯.

4 重视书写表达,做到条理清晰论证严谨,提升学生的数学素养

立体几何的解答题往往分为证明和求解两个部分,前者主要考查学生的逻辑推理,部分学生在论证过程中字迹书写潦草不易辨认,或者书写过程词不达意,符号和定理乱用；没有思考成熟一边写一边改动,卷面欠缺整洁；当然也有学生答题没有信心,对论证缺乏一个整体的解决方案,写到哪里算哪里.这些现象导致严谨性不够而失分,因此教师需要在平常的教学中做到示范引领,如设定一个基本长度时要用“不妨设”或“不失一般性设”等字眼,明确推理过程是否可以“同理”,书写中慎用“易证”、“易得”等字眼,在新一届的备考训练中,需让学生明确该类问题的证明重心或求解关键点在哪里,明确几种常规的处理手段,通过实践来改进我们的教学策略和提高教学效率.