2020年高考全国卷三角试题评析及备考建议*

广东省中山市教育教学研究室(528400) 方 勇

2020年高考全国卷三角试题注重对三角函数、三角恒等变换、解三角形等必备知识的考查,着重考查空间想象能力和数学运算能力,对教学发挥了正确导向作用,贯彻落实了《中国高考评价体系》中的相关设想.

一、考查必备知识

数学科必备知识是指即将进入高等学校的学习者在面对与数学相关的生活实践或学习探索问题情境时,高质量地认识问题、分析问题、解决问题所必须具备的数学知识.三角学是数学的经典内容和重要工具,是沟通几何与代数的桥梁,其内容蕴含了数形结合等重要的数学思想方法,体现了数学学科的本质特征,是数学知识体系中的菁华.就中学来讲,三角是中学数学课程体系的重点内容,它既是初中三角形知识的拓展与延伸,又是学习高等数学的必备基础.因此,历年高考都注重对三角知识的考察,每份卷以三角学知识为考点的试题的分值稳定保持在15 分左右.

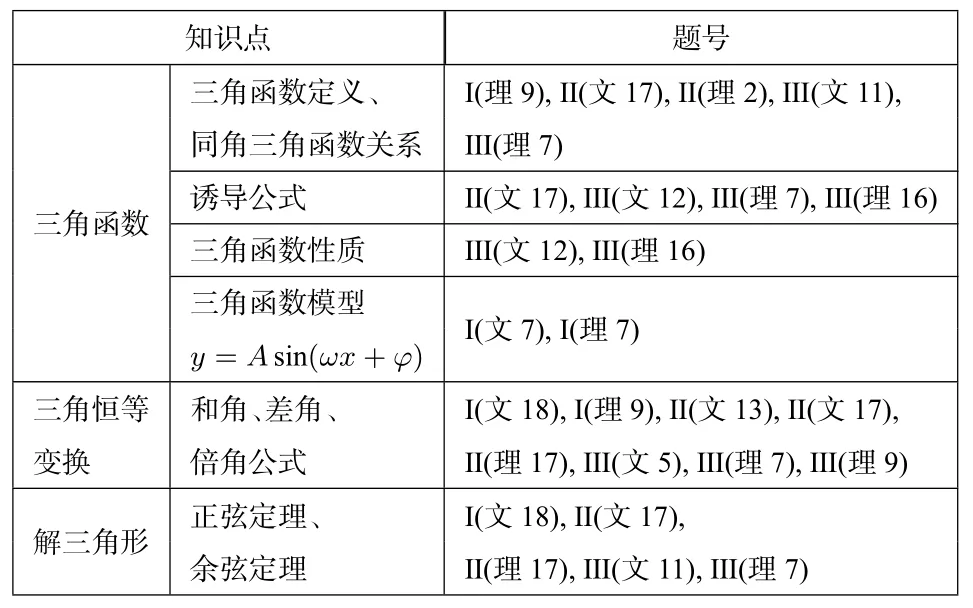
2020年高考全国卷三角部分知识考查分布如下表：

知识点题号_______________三角函数定义、Ⅰ(理9),Ⅱ(文17),Ⅱ(理2),Ⅲ(文11),同角三角函数关系Ⅲ(理7)___________________________三角函数诱导公式Ⅱ(文17),Ⅲ(文12),Ⅲ(理7),Ⅲ(理16)三角函数性质Ⅲ(文12),Ⅲ(理16)_________________三角函数模型y=A sin(ωx+φ)Ⅰ(文7),Ⅰ(理7)三角恒等和角、差角、Ⅰ(文18),Ⅰ(理9),Ⅱ(文13),Ⅱ(文17),变换倍角公式Ⅱ(理17),Ⅲ(文5),Ⅲ(理7),Ⅲ(理9)___解三角形正弦定理、Ⅰ(文18),Ⅱ(文17),余弦定理Ⅱ(理17),Ⅲ(文11),Ⅲ(理7)__________

从上表可以看出,2020年高考全国卷数学试题对三角知识的考查,有以下特点：

(1)考查主干知识2020年高考全国卷对三角知识的考查的特点之一便是以三角学中主干知识作为考查重点,主要考查三角函数定义、同角三角函数关系、诱导公式、三角函数及三角模型性质,重点考查两角和与差的三角函数公式、正弦定理和余弦定理及其应用.

(2)考查形式灵活2020年高考全国卷试题采取了灵活多样的形式对三角知识进行考查.在题型上既有选择题,也有填空题和解答题,甚至还出现了多项选择填空题(Ⅲ(理16)),采取这种开放式新题型的考查形式是为向新高考过渡做好铺垫.在试题编排上,Ⅰ卷文理科有一道共用试题(Ⅰ(文7),Ⅰ(理7)),Ⅲ卷文科第11 题和Ⅲ卷理科第7 题采取了同题干,但所求问题不同的考查形式,Ⅲ卷文科第12 题和Ⅲ卷理科第16 题题干相同,四个选项只有一项不同,但文科中设置为单项选择,理科设置为多项选择(多选填空).总体来看,因使用Ⅰ卷的省份明年将大部分实行不分文理科的新高考,故Ⅰ卷在逐渐减少文理科卷之间的差别,而使用Ⅲ卷的省份进入新高考稍晚,故试题编排上还继续保持着文理科两卷的差异性.

(3)考查层次多样为体现疫情时期对考生的人文关怀,今年高考全国卷三角试题整体难度较上一年有较大降低,但命题者通过精心设计,仍实现了难度上的多层次考查,既有对三角函数定义、公式的简单考查(如Ⅰ(理9),Ⅱ(文13),Ⅱ(理2),Ⅲ(理9)等题),亦有对三角恒等变换、正弦定理、余弦定理等知识的基础性考查(如Ⅰ(文18),Ⅱ(文17),Ⅱ(理17)等题),还有对三角函数性质的综合性考查(如Ⅲ(文12),Ⅲ(理16)等题).综合今年全国卷来看,三角试题在难度设计上保有层次性,在思维的灵活性、深刻性,方法的综合性、探究性上保有区分度,发挥了服务选才的功能.

二、考查关键能力

数学关键能力是指即将进入高等学校的学习者在面对与数学相关的生活实践或学习探索问题情境时,高质量地认识问题、分析问题、解决问题所必须具备的能力.抽象的数学关键能力包括知识获取能力、实践操作能力、思维认知能力等,而空间想象能力、数学运算能力、推理论证能力、抽象概括能力等则是数学关键能力的具体表现.

2020年高考全国卷三角试题着重考查学生的空间想象能力和数学运算能力.

(1)空间想象能力空间想象能力是对空间形式的观察、分析、抽象的能力,主要表现为识图、画图和对图形的想象能力.识图是指观察研究所给图形中的几何元素之间的相互关系；画图是指将文字语言和符号语言转化为图形语言以及对图形添加辅助图形或对图形进行各种变换；对图形的想象则是空间想象能力的高层次要求.

题目1(Ⅰ(文7),Ⅰ(理7))设函数在[-π,π]的图像大致如下图,则f(x)的最小正周期为( )

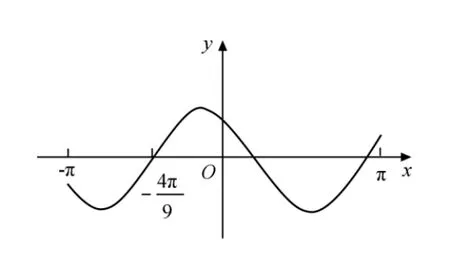
解法1函数图象过点即又是函数f(x)图象与x轴负半轴的第一个交点,所以解得：则函数f(x)的最小正周期为故选C.

解法2函数图象过点即所以ℤ,解得ω=又由图像可知π＜T＜2π,即则1＜ω＜2,所以ω=则函数f(x)的最小正周期为故选C.

评析本题以三角函数模型y=Acos(ωx+φ) 为载体,考察学生识图、用图的能力.解法1 需要考生识别出点是函数f(x)图象与x轴负半轴的第一个交点,则由余弦函数图像变换性质可知从而求出ω的值及函数的周期.解法2 利用余弦函数的零点求出ω的一般值,再结合题目所给图形特殊点位置,判断出函数周期π＜T＜2π,从而确定ω的准确值.两种解法均需要考生能正确识别图形中几何元素的位置关系并能用代数关系式描述出来,考查学生“形数结合”的能力.

题目2(Ⅲ(文12))已知函数f(x)=则( )

A.f(x)的最小值为2

B.f(x)的图像关于y轴对称

C.f(x)的图像关于直线x=π对称

D.f(x)的图像关于直线x=对称

(Ⅲ(理16))关于函数f(x)=sinx+有如下四个命题：

①f(x)的图像关于y轴对称.

②f(x)的图像关于原点对称.

③f(x)的图像关于直线x=对称.

④f(x)的最小值为2.

其中所有真命题的序号是____.

解函数f(x)的定义域为{ℤ},定义域关于原点对称,又

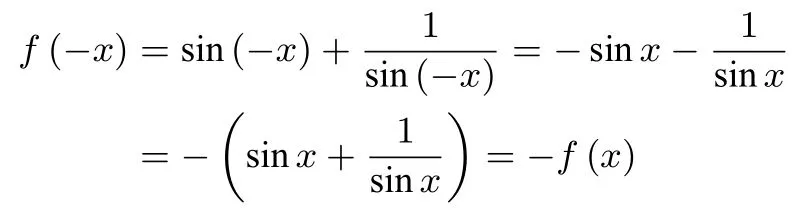
故函数f(x) 为奇函数,其图象关于原点对称,选项B错误,命题①错误,命题②正确；当sinx＜0 时,f(x)=选项A 错误,命题④错误；

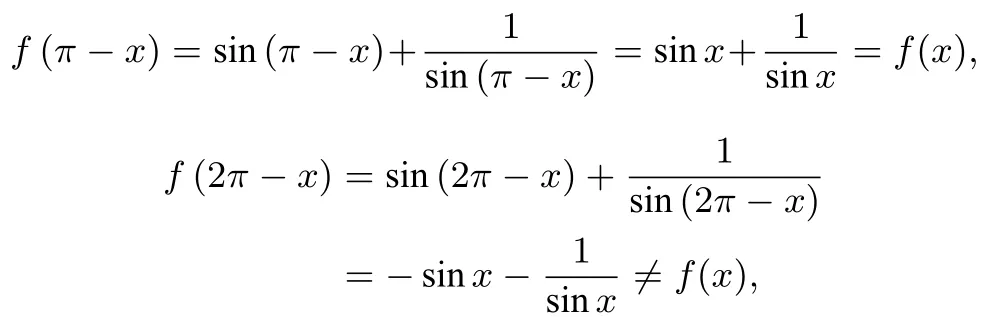
故f(x)的图像关于直线x=对称,不关于x=π对称.选项C 错误,选项D 正确,命题③正确；

评析本题以学生熟悉的正弦函数为切入点,综合考查复合函数的性质：对称性(奇偶性)、最值等.本题的难点在于考查学生对对称性的理解.图形对称是几何直观,但与上题不同的是,本题并没有给出几何图形,学生也很难作出本题函数图形,必须借助代数工具来探究函数的对称性.这就要求学生能够用代数式来刻画几何直观,考查学生对数学语言(图形语言、符号语言)的理解和灵活运用能力.

(2)数学运算能力数学运算能力是指在明晰运算对象的基础上,依据运算法则解决数学问题的能力.普通高中数学课程标准关于数学运算的四个主要表现为：理解运算对象、掌握运算法则、探究运算思路、求得运算结果.三角函数因其性质多样,变换灵活,一直是高中数学运算的难点内容之一,亦是高考考查数学运算能力的良好载体.下面以2020年高考全国Ⅰ卷文科18 题为例说明高考对数学运算能力的考查实践.

题目3(Ⅰ(文18))ΔABC的内角A,B,C的对边分别为a,b,c.已知B=150°.

第一问解法1由余弦定理,b2=a2+c2-2accosB,由条件得,28=3c2+c2-2××cos 150°,即28=4c2-解得c=-2(舍去),c=2,从而a=则ΔABC的面积为

第一问解法2由正弦定理得sinA=因为A+B+C=180°,所以A=30°-C.故sin(30°-C)=化简得=cosC,又sin2C+cos2C=1,解得sinC=由正弦定理解得c=2.则ΔABC的面积为

第一问解法3过C点做AB的垂线交AB的延长线于一点D(如图) 则CD=由b2=CD2+(BD+c)2解得c=2,ΔABC的面积为

第二问解法1在ΔABC中A=30°-C,故

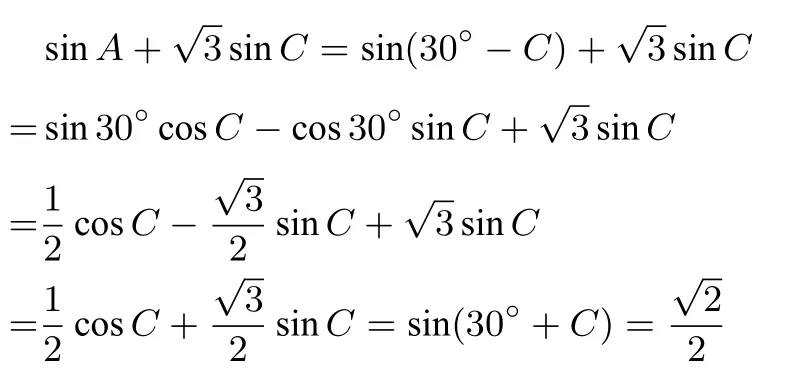
而0°＜C＜30°,所以30°+C=45°,故C=15°.

注也可以由sin(30°+C)=得cos(30°+C)=从而sinC=sin[(30°+C)-30°]=sin(30°+C)cos 30°-cos(30°+C)sin 30°=故C=15°.

第二问解法2在ΔABC中C=30°-A,故

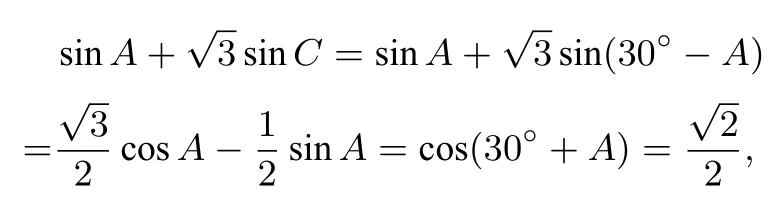
而0°＜A＜30°,所以30°+A=45°,故A=15°,则C=15°.

第二问解法3在ΔABC中A=30°-C,故

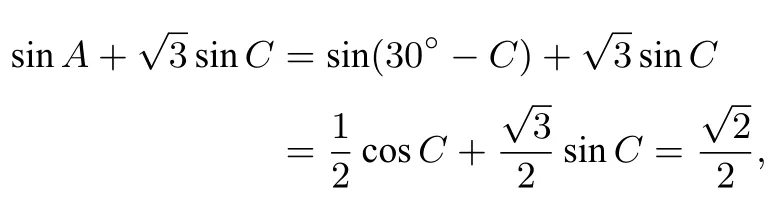
结合上述试题,2020年高考全国卷三角试题对学生数学运算能力的考查,体现在以下几个方面：

(1)要求学生能在数学情境中确定运算对象,提出运算问题.

理解并确定运算对象,提出运算问题是发展数学运算能力的基础.对运算对象的理解角度不同,可能会提出不同的运算问题.如上题中,对于第一问条件a=解法1、3 是从三角形边的关系来理解,解法2 侧重从三角形角的关系来理解.两种不同的理解角度,导致提出不同的运算问题,解法1、3 侧重于求边,解法2 侧重于求角.

(2)要求考生能够针对运算问题,合理选择运算方法、设计运算程序.

运算能力是思维能力和运算技能的结合,主要体现在是否能根据问题的条件选择或设计合理、简捷的运算路径与方法.运算路径、方法设计不合理可能导致的问题有：运算无法进行、运算难度增加、其它新增问题等.如上题第二问中,面对关系式有的考生选择利用两角和公式进行化简(见上文第二问解法1、2),但也有很大一部分考生选择利用同角三角函数关系(sin2C+cos2C=1)建立方程组求解(见上文第二问解法3).从算理上来讲,两种运算路径均是科学的、合理的,但从简捷程度上来讲,两种算法差别较大.建立方程组求解时,涉及到根式运算、消元化简、解一元二次方程等运算过程.从阅卷反馈的情况来看,非常多的考生在这些环节出现运算错误,导致失分.另外,采用这种途径求解,还导致前面所说的其它新增问题——解方程出现多解.而且,这道题的结果不是常见的特殊角,许多考生对数字不敏感,联想不到特殊角.许多考生得到两个解后,心里感觉不踏实,直觉告诉他们应该要舍掉一个解,但是要舍掉多余的解需要在题目中找隐含条件进行讨论,这无端增加了解题的繁琐程度.从答卷情况来看,不少考生没有讨论多解的情况或者采取直接蒙一个答案的做法,从而导致失分.需要指出的是,这道题第二问与2019年全国高考数学Ⅰ卷理科17 题考查要求异曲同工,考生在运算过程中暴露的问题几乎一样,实在令人遗憾.

(3)要求考生能够依据法则、公式进行正确运算、变形和数据处理.

运算法则、公式是运算的依据,是推理的基础,也是运算结果具有唯一性的保障.正确运用运算法则、公式进行运算是发展运算能力的基础.三角恒等变换灵活多样,是考查数学运算能力的良好载体.如本题第二问解法1、2 中,需对式子sin(30°-C)+(或sinA+运用两角和、差公式进行恒等变换.从答卷情况来看,许多考生运算基本功不扎实,出现了形形色色的错误,比如出现sin(30°-C)+=sin(60°+C)或sin(30°-C)+=sin(60°-C)或sin(30°-C)+=cos(60°+C)等变形错误.同上文(2)中所述,这种运算问题在去年Ⅰ卷理科17 题中已经充分暴露,但从考生答卷情况来看,并无明显改善.这说明我们平时教学中,对于学生运算要求并没有落到实处.

三、备考建议

2020年高考全国卷三角试题重视考查学生对必备知识和关键能力的掌握,注重考查学生的思维能力和学习潜能,对教学发挥了正确的导向作用.从答卷情况来看,我们在教学中需要注意下面两个问题：

(1)注重落实“双基”.新课程改革关注发展学生数学科核心素养,但落实“双基”并不是过时了,恰恰相反,落实“双基”是发展学生核心素养的的前提条件.学生必须掌握基本知识、基本技能,在运用基本知识、基本技能解决数学问题的过程中,发展数学能力,积累解决数学问题的经验,并将这些经验内化为数学思维品质.在此过程中,学生逐渐形成良好的情感态度和数学价值观,数学素养得到发展.从本题阅卷情况来看,很多考生暴露出了基本知识不熟悉、基本技能没掌握的情况,而且这些问题在上一年已经出现,说明这些问题并没有引起教师们的足够重视,教学中浮在表面、缺少实效的情况仍然严重,急需改进.

(2)注重发展学生的数学语言能力.数学语言是数学思维的外在体现.要注重数学思维训练和数学语言训练,帮助学生形成有逻辑、有条理、规范、简洁地使用数学语言表达的习惯.数学解题过程的书写就是数学语言表达的一种形式,很多考生在答卷中出现论证不严谨、论述次序混乱,数学符号使用不规范,书写过程繁琐等问题.这些问题的解决需要教师从低年级起就要严格要求,狠抓训练,逐步改进.