2020年高考全国Ⅰ卷函数及导数试题分析及备考建议

广东省惠州市第一中学(516007) 郭慧敏

华南师范大学数学科学学院(5106311) 苏洪雨

历年高考中,“函数与导数”是较为重要,也是较为稳定的考查模块,今年也不例外.其题型设置选择题,填空题,解答题均有；难度分布易,中,难,梯度明显；知识点考查全面,主要涉及：函数模型识别,指对数函数,导数的几何意义及应用,函数单调性研究,函数零点等；将函数与方程,转化与化归,分类与整合,数形结合的数学思想方法贯穿始终；深刻体现了数学建模,逻辑推理,数学运算、直观想象等的数学核心素养.其“稳”且“重”的试题特点,以“秤砣效应”突出了今年试题的均衡与平稳,为数学整体达到高考评价“一核四层四翼”的要求,做出了重要的贡献.

一、2020年全国Ⅰ卷函数与导数试题分布一览表

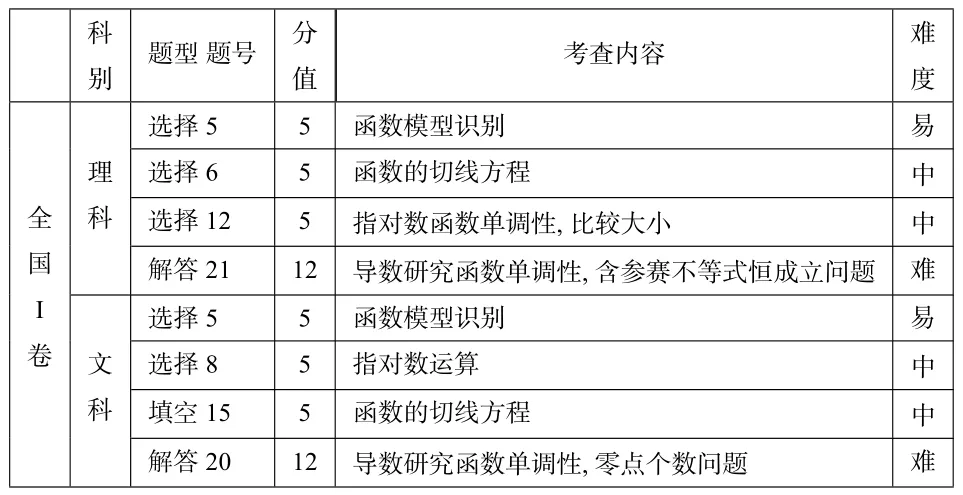
科 别题型题号分 值考查内容难 度选择5 5函数模型识别易理 科选择6 5函数的切线方程中全国Ⅰ卷选择12 5指对数函数单调性,比较大小中解答21 12导数研究函数单调性,含参赛不等式恒成立问题难选择5 5函数模型识别易文 科选择8 5指对数运算中填空15 5函数的切线方程中解答20 12导数研究函数单调性,零点个数问题难

二、2020年函数与导数客观题评析

类型一：函数应用

数学建模活动是课程改革中地位特别突出的内容之一,函数的应用不仅体现在用函数解决数学问题,更重要的是用函数解决实际问题.新课标则明确指出“理解函数模型是描述客观世界中变量关系和规律的重要数学语言和工具.在实际情境中,会选择合适的函数类型刻画现实问题的变化规律”,题目1 正充分体现了过渡阶段,新课程改革的导向性.

题目1(2020 全国Ⅰ卷文理科第5 题)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位：°C)的关系,在20 个不同的温度条件下进行种子发芽实验,由实验数据得到下面的散点图：

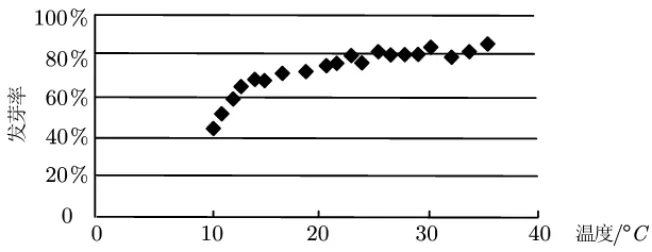
由此散点图,在10°C至40°C之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )

A.y=a+bxB.y=a+bx2

C.y=a+bexD.y=a+blnx

解析由散点图分布可知,散点分布呈现上凸递增的趋势,与选项相应的函数图象比对,A 选项为一次函数,图象呈直线上升趋势；B 选项为二次函数,图象呈下凸上升趋势；C选项为指数型函数,图象下凸上升趋势,且增长速度最快；D选项为对数型函数,图象呈现上凸递增趋势与散点图基本相符,故选D.

类型二、指对数函数指数函数和对数函数是最基本的、应用最广泛的函数,是进一步学习数学的基础.新旧课标相比,对于指对数的运算,及指对数函数的图象和性质的研究没有太大变化.题目2 是文科,主要突出了指对数的运算；题目3 是理科,则更灵活地考查了函数构造,指数对数函数的单调性及应用函数单调性比较大小的问题,文理对比之下,难度设置有区别.

题目2(2020 全国Ⅰ卷文科第8 题)设alog34=2,则4-a=( )

解析由alog34=2 得log34a=2=log39,故4a=9,所以有4-a=故答案为B.

例3(2020 全国Ⅰ卷理科第12 题)若2a+log2a=4b+2log4b,则( )

A.a＞2bB.a＜2bC.a＞b2D.a＜b2

解析构造函数f(x)=2x+log2x,则f(x)为增函数,因为2a+log2a=4b+2log4b=4b+log2b,所以

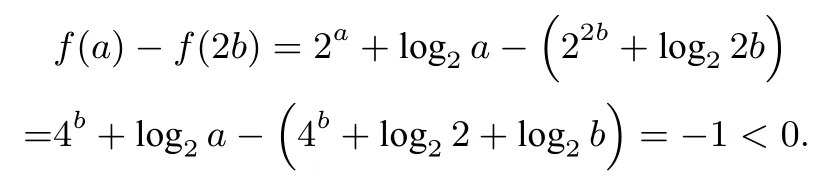
因此f(a)＜f(2b),故a＜2b.因为2a+log2a=4b+2log4b=22b+log2b,从而

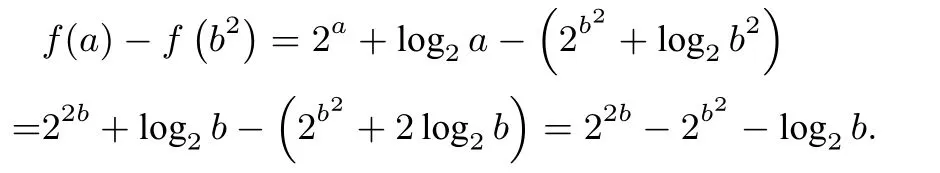
当b=1 时,f(a)-f(b2)=2＞0,此时f(a)＞f(b2),有a＞b2；当b=2 时,f(a)-f(b2)=-1＜0,此时f(a)＜f(b2),有a＜b2.因此C、D 不符合题意,故答案为B.

类型三、函数的切线方程

导数是微积分的核心内容之一,学生通过丰富的实际背景理解导数的概念,函数切线的斜率则是导数概念的几何化表现,对比新旧课标,两者描述相同：“通过函数图象直观理解导数的几何意义”,故掌握用导数求函数在某点处的切线方程是高考中较为稳定的考查点,题目4,5 均体现了这一要求.

题目4(2020 全国Ⅰ卷理科第6 题)函数f(x)=x4-2x3的图象在点(1,f(1))处的切线方程为( )

A.y=-2x-1 B.y=-2x+1

C.y=2x-3 D.y=2x+1

解析f(x)=x4-2x3,f′(x)=4x3-6x2,f(1)=-1,切点为(1,-1),切线斜率为f′(1)=-2,所求切线的方程为y+1=-2(x-1),即y=-2x+1.故答案为B.

题目5(2020 全国Ⅰ卷文科第15 题)曲线y=lnx+x+1的一条切线的斜率为2,则该切线的方程为____.

解析设切线的切点坐标为(x0,y0),y=lnx+x+1,y′=+1,所以切线斜率为+1=2,解得x0=1,y0=2,所以切点坐标为(1,2),由点斜式得切线方程为y-1=2(x-1),即y=2x-1.

三、2020年函数与导数解答题评析

历年高考,函数与导数的解答题都是压轴之作,因为其综合了多个方面的知识,蕴含了丰富的数学思想方法,能从多层次,多维度考查学生的能力.今年的函数与导数解答题,文科是将指数函数和含参一次函数作差,组合成新函数,讨论其单调性和零点个数；理科则是将指数函数和含参二次及三次函数组合,讨论单调性和研究含参不等式恒成立条件.两题都具有起点低,落差大,满分难的共同特点,在参数的研究上有相似之处.充分考查了学生在代数运算,数形结合,极限思想上的数学能力,让每个层次学生的能力都能得到真实的体现.

题目6(2020 全国Ⅰ卷文科第20 题)已知函数f(x)=ex-a(x+2).

(1)当a=1 时,讨论f(x)的单调性；

(2)若f(x)有两个零点,求a的取值范围.

第一问解析.给出a=1,通过求导,研究导数与0 的关系,即可得出答案.考查基础知识和能力,是起点较低的一问,具体解答如下：

(1)当a=1 时,f(x)=ex-(x+2),f′(x)=ex-1,令f′(x)=0,得x=0.

当x＜0 时,f′(x)＜0,f(x)在(-∞,0)上单调递减；当x＞0 时,f′(x)＞0,f(x)在(0,+∞)上单调递增.

第二问解析.结合参数a,讨论零点个数,从参数与变量的关系可从“不分参”,“局部分参”及“完全分参”三种思路进行解析,具体分析如下：

方法一(不分参：带参讨论函数最值与零的关系.)f′(x)=ex-a,当a≤0 时,f′(x)＞0,所 以f(x) 在(-∞,+∞)单调递增,故f(x)至多存在1 个零点,不合题意.当a＞0 时,令f′(x)=0 可得x=lna,当x ∈(-∞,lna)时,f′(x)＜0,当x ∈(lna,+∞)时,f′(x)＞0,所以f(x)在(-∞,lna)单调递减,在(lna,+∞)单调递增,故当x=lna时,f(x)取得最小值,最小值为f(lna)=-a(1+lna).

(i)若0＜a≤则f(lna) ≥0,f(x)在(-∞,+∞)至多存在1 个零点,不合题意；

(ii) 若a＞则f(lna)＜0,由于f(-2)=e-2＞0,所以f(x) 在(-∞,lna) 存在唯一零点.f(2a)=e2a-a(2a+2)=e2a-2a(a+1),下证ex≥x+1：

构造函数g(x)=ex-(x+1),g′(x)=ex-1,x ∈(-∞,0),g′(x)＜0,x ∈(0,+∞),g′(x)＞0,g(x)在(-∞,0) 单调递减,在(0,+∞) 单调递增,故g(x)min=g(0)=0,所以ex≥x+1,所以ea≥a+1＞0,ea-1≥a＞0,则e2a=e·ea-1·ea≥e·a·(a+1)＞2a(a+1),即f(2a)＞0,且2a＞lna,故f(x)在(lna,+∞)存在唯一零点,从而f(x)在(-∞,+∞)上有两个零点.

综上,a的取值范围是

方法二(局部分参：讨论指数函数图象与一次函数直线交点个数.)f(x)=0,即ex=a(x+2),y=f(x)的零点个数即为y=ex与y=a(x+2)交点的个数.y=a(x+2)恒过点(-2,0).

下求y=ex过点(-2,0) 的切线斜率：设切点为(x0,y0),则切线的斜率k=因为(ex)′=ex,所以切线的斜率k=ex0,即有ex0=解得x0=-1,故k=e-1.

当a ∈时,f(x) 在(-∞,+∞) 上无零点；当a=或a ∈(-∞,0) 时,f(x) 在(-∞,+∞) 上有一个零点；当a ∈时,由于y=ex为下凸递增函数,y=a(x+2)为直线,以相切为参照,当直线斜率a＞时,两图象有两个交点,即f(x)在(-∞,+∞)上有两个零点.

综上,a的取值范围是

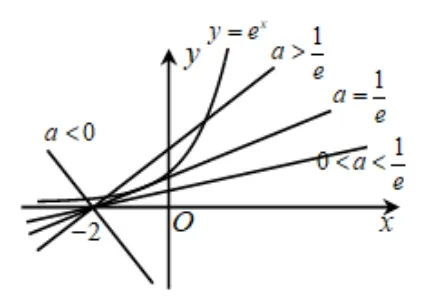
图1

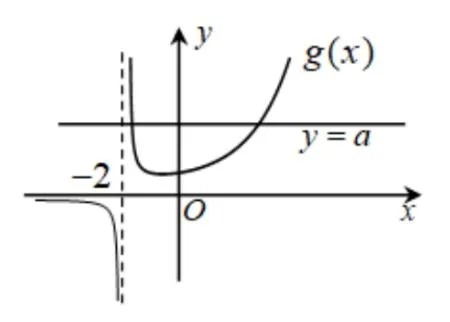
图2

方法三(完全分参：研究不含参数的新函数图象.)f(-2)=e-2≠ 0.在x≠-2 的前提下,f(x)=0,即a=y=f(x) 的零点个数即为y=a与g(x)=(x≠-2)交点的个数.

g′(x)=当x＜-2 时,g′(x)＜0,y=g(x) 在(-∞,-2) 上递减,且g(x)=＜0；当-2＜x≤-1 时,g′(x) ≤0,y=g(x)在(-2,-1]上递减,且当x＞-1时,g′(x)＞0,y=g(x)在(-1,+∞)上递增,且由洛必达法则,

综上可得g(x)=示意图,由图2可知：当时,f(x)在(-∞,+∞)上有两个零点.

题目7(2020 全国Ⅰ卷理科第21 题)已知函数f(x)=ex+ax2-x.

(1)当a=1 时,讨论函数f(x)的单调性；

(2)当x≥0 时,f(x) ≥+1 恒成立,求a的取值范围.

第一问解析给出a=1,通过求导,研究导数与0 的关系,即可得出答案,考查基础知识和能力,和文科20 题如出一辙,同样是起点较低的一问.具体解答如下：

a=1 时,f(x)=ex+x2-x,f′(x)=ex+2x-1.当x ∈(-∞,0)时,f′(x)＜0；当x ∈(0,+∞)时,f′(x)＞0.所以f(x)在(-∞,0)单调递减,在(0,+∞)上单调递增.

第二问解析含参不等式恒成立,求参数a范围的问题,可转化为研究或讨论函数的最值问题.如何分析函数的最值呢? 和文科20 题一样,以参数与变量的关系,可从“不分参”,“局部分参”及“完全分参”三种思路进行思考.

方法一(不分参：带参分类讨论函数的最值.)f(x) ≥+1 等价于设函数则

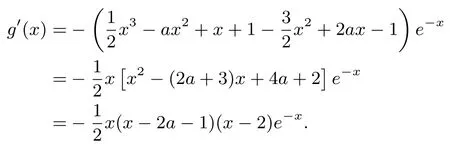
(i)若2a+1 ≤0,即a≤则当x ∈(0,2) 时,g′(x)＞0.所以g(x) 在(0,2) 上单调递增,而g(0)=1.故当x ∈(0,2)时,g(x)＞1,不合题意.

(ii)若0＜2a+1＜2,即则当x ∈(0,2a+1)∪(2,+∞)时,g′(x)＜0；当x ∈(2a+1,2)时,g′(x)＞0.所以g(x)在(0,2a+1),(2,+∞)上单调递减,在(2a+1,2)上单调递增.

由于g(0)=1,所以g(x) ≤ 1,当且仅当g(2)=(7-4a)e-2≤1,即a≥所以当时,g(x)≤1.

(iii)若2a+1 ≥2,即a≥此时x ∈(0,2)∪(2a+1,+∞),g′(x)＜0,函数g(x)在(0,2),(2a+1,+∞)上单调递减；x ∈(2,2a+1),g′(x)＞0,g(x)在(2,2a+1)单调递增.

注意到g(0)=1,g(2a+1)=下面证明x≥时,因而h(x) 在单调递减,又从而时,g(2a+1)≤1.

综上,a的取值范围为

方法二(局部分参：讨论新函数图象与一次函数直线交点个数.) 对任意的x≥0,f(x) ≥+1 等价于则

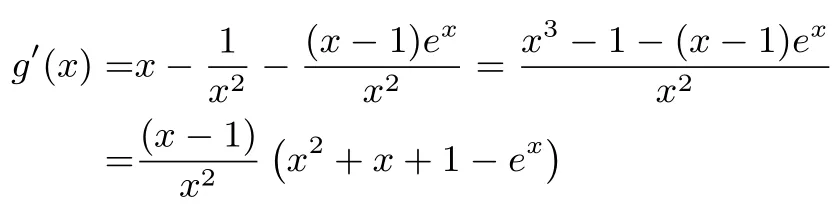
令φ(x)=x2+x+1-ex,则φ′(x)=2x+1-ex,φ′′(x)=2-ex.当x ∈(0,ln 2) 时,φ′′(x)＞0,φ′(x) 在(0,ln 2)上单调递增；当x ∈(ln 2,+∞)时,φ′′(x)＜0,φ′(x)在(ln 2,+∞)上单调递减.

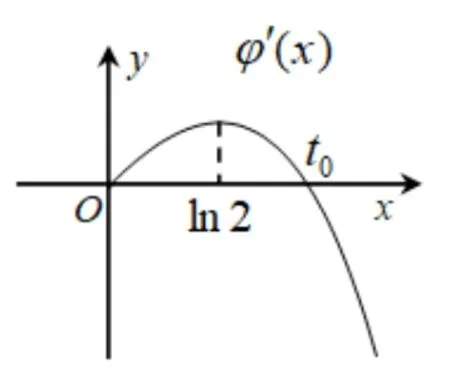
图3

因为φ′(0)=0,x→+∞,φ′(x)→-∞,φ′(x) 的简图如图3所示,存在t0∈(1,2)使得φ′(t0)=0,当x ∈(0,t0) 时,φ′(x)＞0,所以φ(x) 在(0,t0)上递增；当x ∈(t0,+∞) 时,φ′(x)＜0,所以φ(x)在(t0,+∞)上递减.

又因为φ(0)=0,x→+∞,φ(x)→-∞,因为φ(1)=3-e＞0,φ(2)=7-e2＜0,φ(x) 的简图如图4所示,存在x0∈(1,2),使得φ(x0)=0.令g′(x)=0,得x=1,或x=x0,所以当x ∈(0,1)时,g′(x)＜0,函数g(x)在(0,1)上单调递减；当x ∈(1,x0)时,g′(x)＞0,函数g(x)在(1,x0)上单调递增；当x ∈(x0,+∞)时,g′(x)＜0,函数g(x)在(x0,+∞)上单调递减.

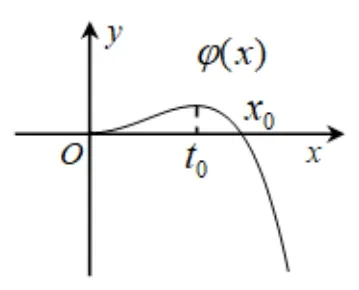
图4

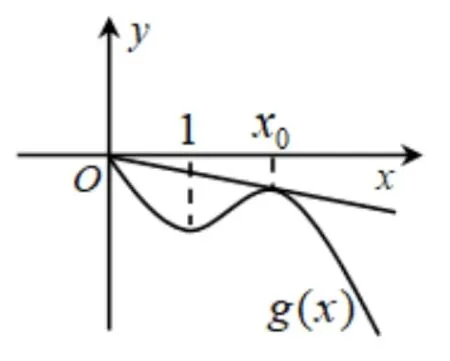
图5

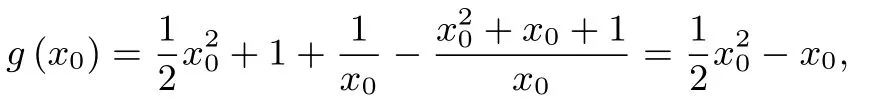
因为x0∈(1,2),g(x0)＜0,设直线y=bx与函数y=g(x)相切,切点为(x1,g(x1)),则切线方程为

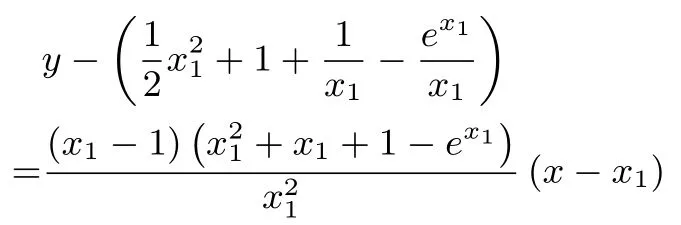
因为切线过原点,所以

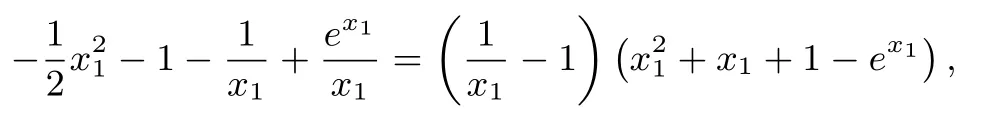
构造函数易证ex1--x1-1＞0.所以x1=2,此时b=所以a≥

方法三(完全分参：研究不含参数的新函数形态.) 对∀x≥0,f(x)≥+1 等价于ax2≥+x+1-ex.当x=0 时,不等式对任意的a都成立,当x＞0 时,

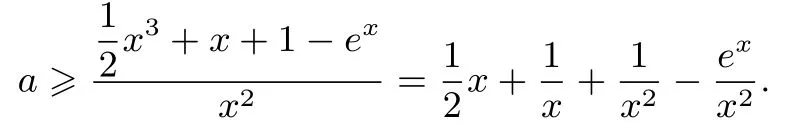
令g(x)=则g′(x)=

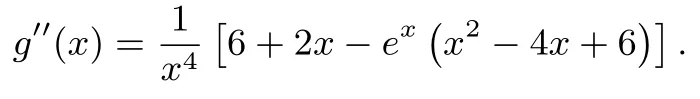
令φ(x)=6+2x-ex(x2-4x+6),x＞0,则φ′(x)=2-ex(x2-2x+2),φ′(0)=0,φ′′(x)=-x2ex≤0,φ′(x)在(0,+∞) 上递减,于是φ′(x) ≤φ′(0)=0,所以φ(x)在(0,+∞) 上递减,所以φ(x) ≤φ(0)=0,于是g′′(x)＜0,g′(x)在(0,+∞)上单调递减.而g′(2)==0,x ∈(0,2) 时,g′(x)＞0,g(x)递增；x ∈(2,+∞) 时,g′(x)＜0,g(x) 递减.所以g(x)max=g(2)=故

综合评析

题目6 和题目7 都是含参数的函数问题.解决这类问题,以参数与变量的关系,可从“不分参”,“局部分参”及“完全分参”三种思路进行思考.

“不分参”,即是以导数为工具,带着参数去讨论函数的形态,进而分析每种情况中的单调区间、最值或零点等问题.这种思路是最直接的,但往往也是较繁杂的,其困难在于,参数a分类讨论的依据是什么? 导函数的是否有零点,零点的个数,零点的大小往往是常见的分类标准；若需研究函数的最值,就需进一步分类讨论区间端点的函数值与函数的极值的大小.讨论依据越多,分类情况越复杂,题目难度也就越大.

“局部分参”,即是通过函数与方程,不等式的关系,将一个函数分解两个新函数,一个带参数,一个不带参数.“局部分参”的思考点在于,如何分离重组两个新函数,才能使得分类讨论最优化? 若能分离出一个直线函数,另一个曲线函数,并且将参数放在直线函数上,这就是关键技巧所在.接着,通过数形结合将问题转化为直线与曲线图像关系的研究,此时“相切”往往是分类讨论的临界状态.“局部分参”通过图像分析优化了分类讨论,但此法具有“先天缺陷”,图像分析只能辅助解题,不能代替数学的严谨推理分析,尽管对图形特征进行描述,也并非就十分周全.

“完全分参”,即是通过恒等变形,把原来的函数中的参数独立分离出,把参数看成一个常数函数,把不含参数的部分看成一个新函数.只研究不含参的新函数形态,进而通过图像分析,探究问题的结论.这种方法的困难在于,新函数虽不含参数,但形式会比较复杂,求导运算量较大；求导函数零点时,常常要面对解超越方程的困难；通过导函数分析图像时,也往往要分析函数的极限,这就需要借助更多灵活的方法,如多次求导、虚设零点、洛必达法则求极限等.

综上分析,含参数的函数问题的三种思路各有利弊,需要结合题目特点,学生的认知水平进行选择和使用.

四、教学与备考建议

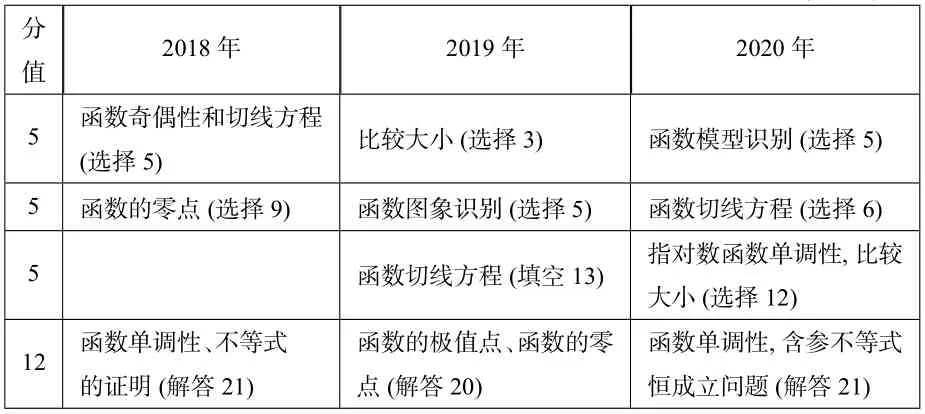
表1：近三年全国Ⅰ卷函数与导数试题考点与分值统计表(理科)

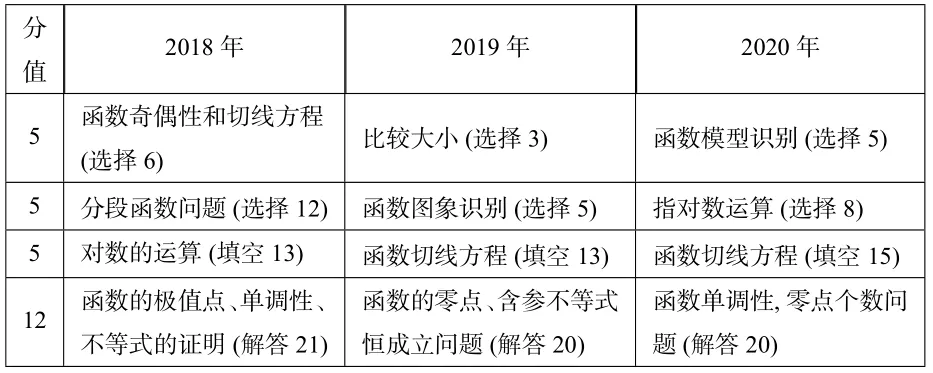
表2：近三年全国Ⅰ卷函数与导数试题考点与分值统计表(文科)

通过对比近三年全国Ⅰ卷函数与导数试题考点,可以发现：全国Ⅰ卷对函数与导数内容的考查总体稳定,层次分明,主要考查关键词为：函数图象(模型),切线方程,指对数函数,比较大小、零点、单调性、含参不等式恒成立等.结合此对比分析,我们给出如下教学和备考建议：

(一)认真研究新课标,准确把握方向

近几年是新课程标准实施的过渡时期,新的高考制度下,没有了《考试大纲》的参考,课程标准是唯一的命题依据.在“函数与导数”模块上,将新旧课标对比,变化如下：

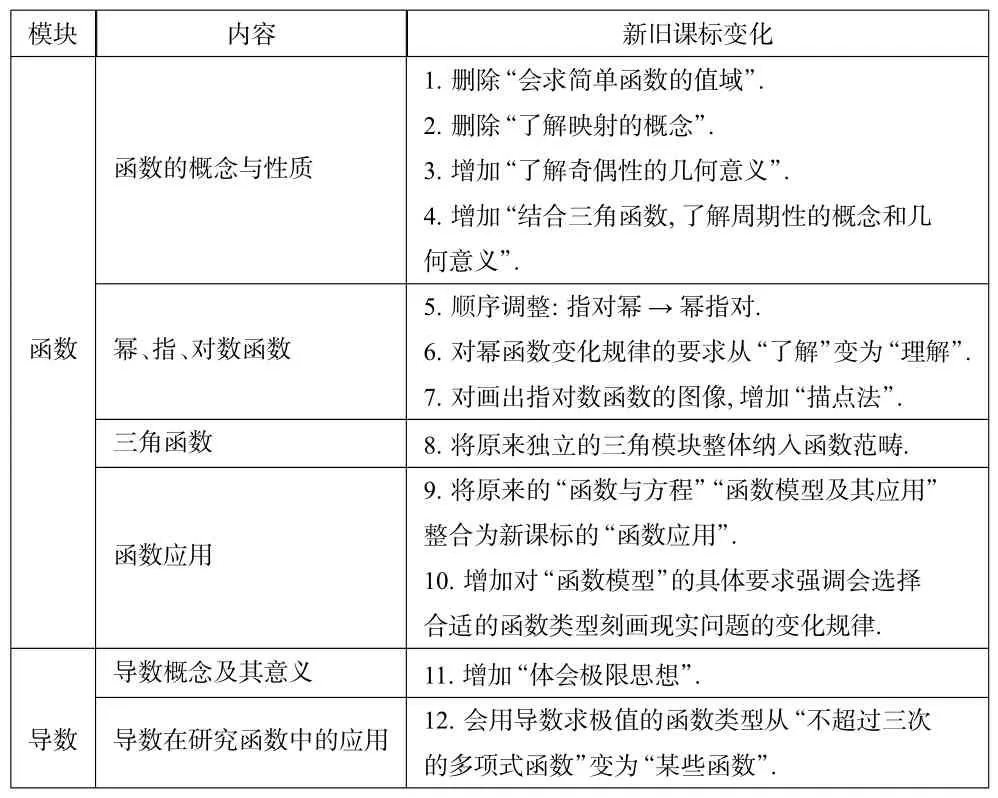
模块内容新旧课标变化_________________函数的概念与性质1.删除“会求简单函数的值域”.2.删除“了解映射的概念”.3.增加“了解奇偶性的几何意义”.4.增加“结合三角函数,了解周期性的概念和几____________________________________________________________________________________________何意义”.函数幂、指、对数函数5.顺序调整：指对幂→幂指对.6.对幂函数变化规律的要求从“了解”变为“理解”.7.对画出指对数函数的图像,增加“描点法”.______三角函数8.将原来独立的三角模块整体纳入函数范畴.______函数应用9.将原来的“函数与方程”“函数模型及其应用”整合为新课标的“函数应用”.10.增加对“函数模型”的具体要求强调会选择合适的函数类型刻画现实问题的变化规律.________导数概念及其意义11.增加“体会极限思想”.______________________导数导数在研究函数中的应用12.会用导数求极值的函数类型从“不超过三次________________________________________________________________________________________________的多项式函数”变为“某些函数”.

通过以上对比,我们可以发现：幂函数地位的提高,三角函数的整体纳入,函数模型的强调,极限思想的增加等,都是变化较大的关注点.教师在日常的教学和备考中,要积极研究,聚焦关注点,准确把握过渡时期的改革方向.

(二)重视基础知识和基本方法的教学

提到函数与导数,学生总是会联想到难度最大,最不容易得分的题目.但事实上,今年函数与导数的题目中,基础中档难度分值约占70%,这说明函数与导数并非只能“高高在上”的难题,而是可以“袋袋平安”的得分题.而在基础知识和基本方法上,学生的认知和学习能力基本不存在差异,所以在教学和训练过程中,要强调基础知识和基本方法,不可盲目将函数和导数的题目提升难度,将其基础落实到平时的作业和检测中,让学生在学习的过程中获得信心,获得分数.

(三)重视灵活数学思维的培养

函数与导数的问题有着非常丰富数学思想和灵活的数学思维,包括函数与方程,转化与化归,分类与整合,代数与几何,局部与整体等.通过函数与导数的学习和研究,学生思考和解决问题的能力能得到有效的强化和提升.但是,由于函数与导数问题是高考中的较为稳定的考向,已形成了一些固定的解题套路,形成思维定势.思维要“活”,“活”在问题的呈现形式,问题的探究过程,及问题解决方法的开放性,常研究的函数模型,函数零点问题,不等式恒成立问题,参数的分类讨论问题等,可以作为学生思考研究的素材,但不能成为解决问题的模板.学生只有具备了灵活的思维,才能具备独立解决新问题的能力.

(四)重视数学运算能力的落实

数学运算能力是解决数学问题的基本手段,数学六大核心素养之一,在解决函数与导数问题中的尤为重要.数学运算能力表现为：理解运算对象,掌握运算法则,探究运算思路,求得运算结果.例如,今年文理都考查了指对数的运算,此题的考查重点应该是运算的法则；而题目6 第一问,将函数求导后得出导函数零点后,却讨论了原函数的正负,这就是搞错了运算对象；题目7 完全参变分离后,对分离出来的新函数求导,可以从导函数中局部取不同的函数进一步研究,如何是最简便的呢? 这实为运算思路最优化的问题.所以,运算能力的培养,不是一件简单的事,要提升学生的运算能力,不是用一句话“你们自己再算一算! ”就能实现的.

(五)重视高观点下的数学视角

函数和导数,是高等数学的基础,将高等数学中常见的素材简化为中学数学的问题,是常见的试题命制方法,题目6和题目7 中的函数,就是源于高等数学中 的一个常见的泰勒展开式o(xn)(n→∞)；解答过程中图象极限的分析,用到高等数学洛必达法则也能简化答题过程.当然,这并不意味着要过多的将高等数学知识下放到中学教学,而是对教师的专业能力提出更高的要求,教师若能站在高观点下看待问题,找到问题的本质内涵,便能更好地指导中学的数学教学.