2020年高考全国Ⅰ卷不等式选讲试题分析及备考建议

广东省深圳中学(518001) 周峻民

1 试题呈现

题目(2020年高考全国Ⅰ卷文理第23 题) 已知函数f(x)=|3x+1|-2|x-1|.

(1)画出y=f(x)的图像；

(2)求不等式f(x)＞f(x+1)的解集.

该题以分段一次函数的作图与解不等式为载体,体现数形结合、分类讨论、转化与化归等数学思想方法,渗透直观想象、逻辑推理、数学运算等核心素养的考查.

2 试题解答与点评

2.1 试题第(1)问：画出函数y=f(x)图像

解由题意知,函数f(x)=函数y=f(x)图像如图所示：

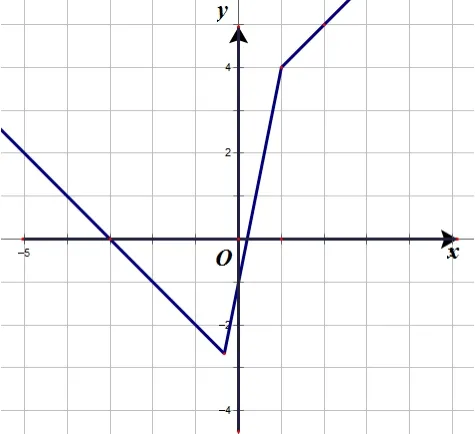
点评本小题设问指向明确,解法单一,通过零点分段法,将含绝对值函数转化为分段一次函数,再根据各段一次函数的图像,画出y=f(x)的图像.

2.2 试题第(2)问：求不等式f(x)＞f(x+1)的解集

解法1(函数图像法)将函数y=f(x)的图像向左平移一个单位长度后得到y=f(x+1)的图像：

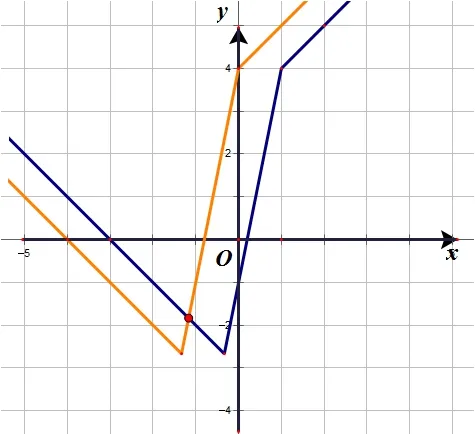
解法2(零点分段法)由题意知f(x+1)=|3x+4|-2|x|,故不等式f(x)＞f(x+1)即为|3x+1|-2|x-1|＞|3x+4|-2|x|.

①当x≤时,-(3x+1)+2(x-1)＞-(3x+4)+2x,即-3＞-4,恒成立,故x≤时原不等式成立；

④当0＜x≤1 时,(3x+1)+2(x-1)＞(3x+4)-2x,即故此时不等式无解；

⑤当x＞1 时,(3x+1)-2(x-1)＞(3x+4)-2x,即3＞4,不成立,故此时不等式无解.

综上所述,不等式f(x)＞f(x+1) 的解集为

解法3(函数单调性法)由第(1)问y=f(x)的图像可知,y=f(x)在上单调递减,在上单调递增.

①当x＜x+1 ≤即时,y=f(x) 在上单调递减,从而f(x)＞f(x+1)恒成立,故

综上所述,f(x)＞f(x+1)的解集为

点评解法1 将不等式问题转化为函数图像的交点问题,体现数形结合思想、直观想象核心素养；解法2 则采用零点分段法去绝对值,直接解不等式,体现了分类讨论思想、数学运算核心素养；解法3 则是利用函数单调性这一函数工具处理不等式问题,体现了转化与化归思想、逻辑推理核心素养.

3 备考建议

3.1 研究高考,把握方向

下面表1、表2分别是近五年全国卷“不等式选讲”的考点分布表、2020年新高考全国卷涉及“不等式选讲”的考点分布表：

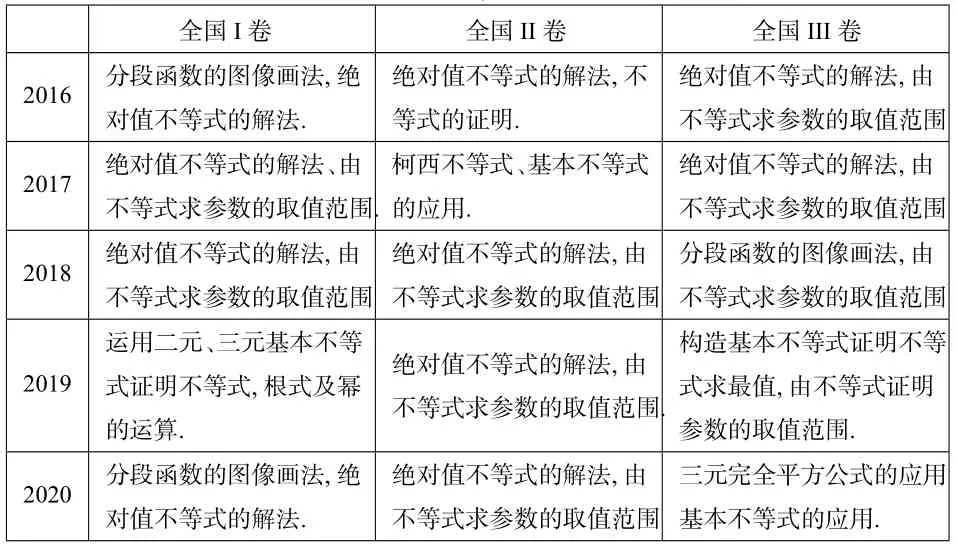
表1：近五年全国卷“不等式选讲”的考点分布表

表2：2020年新高考全国卷涉及“不等式选讲”的考点分布表

从上表可以看出，近五年“不等式选讲”在全国卷中的考点在内容上稳中有变，保持了相当高的稳定性，大部分以考查绝对值不等式为主，穿插考查基本不等式的应用; 2020年新高考全国卷虽然删减了选做题，但并不意味着不间接考查“不等式选讲”的相关内容，例如新高考的全国I卷(山东)第11题与全国II卷(海南)第12题，考查内容涉及到了基本不等式的应用，“不等式选讲”考点依然会在新高考中出现(特别是不等式性质、基本不等式、含绝对值不等式等).

3.2 回归教材，理解本质

许多高三师生对课本不够重视，然而“刷百题不如精教材”，我们应回归教材，追本溯源，从知识的根源——概念、性质人手，并从教材的例题、习题中提炼出一般的通性通法，夯实双基，加强对必备知识的理解和关键能力的训练.

虽然今年是广东高考最后-一次考查“不等式选讲”，但从知识交会角度来看，不等式内容的考查，并不单单立足于“不等式选讲”这道题上，往往是将不等式融合到其他试题中，突出不等式的工具性，淡化其独立性.在备考过程中，要理解不等式的本质，关注其与其他知识在交会处的应用，感悟其中蕴含的思想方法，熟悉不同问题的处理策略，把不等式作为一种解决问题的重要工具，在其他各种不同的知识情境中灵活应用(例如向量、复数的模与绝对值三角不等式，函数的值域、几何最值与基本不等式，函数的单调性与不等式的基本性质等).