2020年高考全国Ⅰ卷数列试题分析及备考建议

广东省云浮市新兴县惠能中学(527400) 郑胜文

数列是高中数学的重要知识模块之一,是历年高考必考内容,也是广大考生“抢分争分”之地.近三年在高考试卷有关数列的试题通常题量是一大或者两小,大题则稳在17 题,与三角考查交替进行,分值约占12 分左右；小题则有1 题基础,另1 题以压轴题形式出现.数列题是考查学生综合素养的重要载体,其蕴含了构造、转化和化归、函数与方程、数形结合等数学思想方法,体现了数学运算、逻辑推理、几何直观等数学学科核心素养.数列备考问题存在题量大、所包含知识面广、题型复杂、难易大小程度区分大且文理不同科考查要求不易把握等情形.近几年的高考都是把数列作为核心内容来考查,从总体上来看,难度虽然有所降低,但是创意不断,而且是常考常新.本文通过对高考全国Ⅰ卷数列题的分析,从文理科数列考题在知识要求、思想方法、能力及核心素养考查等角度进行探讨,旨在为2021 届高三数学数列复习备考提供一个参考,也期望在新高考不分文理科情况下,对教师在进行复习备考时起到一个较为明晰的教学引领和导向作用.

1 试题分析

1.1 试题呈现

题目1(2020年高考全国Ⅰ卷文科第9 题)执行右面的程序框图,则输出的n=

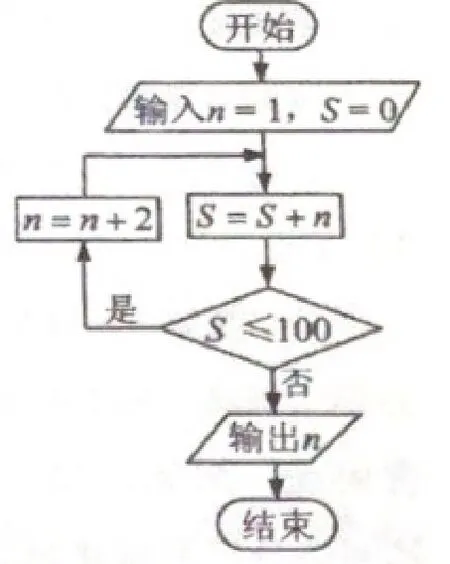
A.17 B.19 C.21 D.23

题目2(2020年高考全国Ⅰ卷文科第10 题) 设{an}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=

A.12 B.24 C.30 D.32

题目3(2020年高考全国Ⅰ卷文科第16 题)数列{an}满足an+2+(-1)nan=3n-1,前16 项和为540,则a1=____.

题目4(2020年高考全国Ⅰ卷理科第17 题)设{an}是公比不为1 的等比数列,a1为a2,a3的等差中项.

(1)求{an}的公比；(2)若a1=1,求数列{nan}的前n项和.

1.2 试题解析

题目1 解析首先对对n,S分别赋值：n=1,S=0,由程序框图得下表：

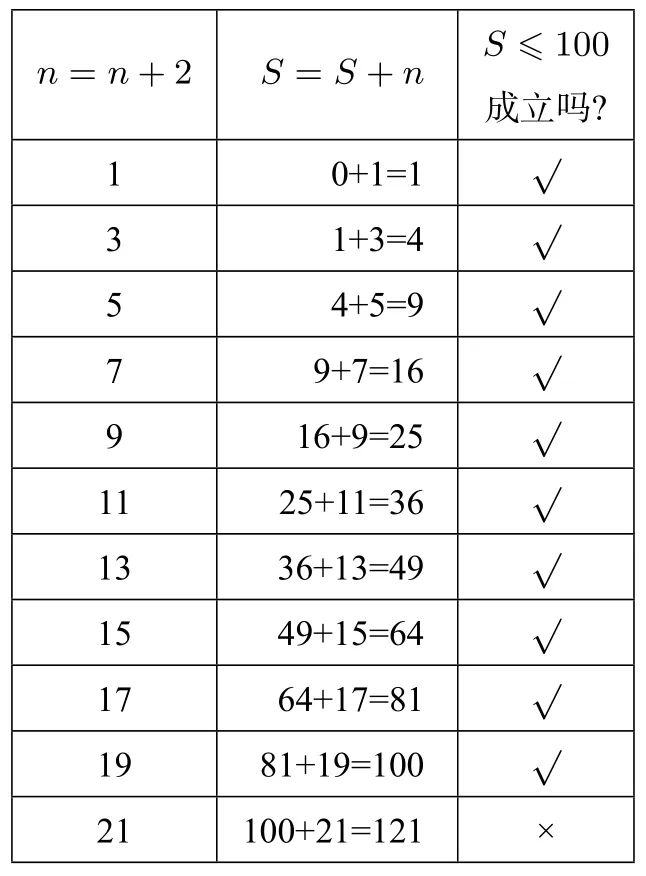
n=n+2 S=S+n S ≤100__________________________成立吗?1 0+1=1√3 1+3=4√5 4+5=9√7 9+7=16√9 16+9=25√11 25+11=36√13 36+13=49√15 49+15=64√17 64+17=81√19 81+19=100√21 100+21=121×____

从上表得知,n=21 是使得S ≤100 不成立的最小正整数,故选C.

另解本题可转化成等差数列来处理问题,由S=S+n得Sk+1=Sk+ak+1,n=n+2 得ak+1=ak+2,其中,a1=1,则ak=2k-1,k ∈ℤ.问题就可以转化成：当Sk＞100 时,求ak的最小值.由且k ∈ℤ,所以k=11,则ak=a11=21,故选C.

题目2 解析由解方程及等比数列基本量来处理.设等比数列{an} 的首项为a1,公比为q,由题设得解得则a6+a7+a8=32.

另解本题可以用整体思想来处理,由题设得解得q=2,a6+a7+a8=(a1+a2+a3)q5=1×32=32.避免繁琐运算.

题目3 解析由an+2+(-1)nan=3n-1,得知需要分奇偶数进行研究,且偶数时只研究部分.

考虑n分别为1,3,5,7,9,11,13,15 时,有a3-a1=2,得a3=2+a1；a5-a3=8,则a5=8+a3=10+a1,同理可得a7=24+a1,a9=44+a1,a11=70+a1,a13=104+a1,a15=140+a1,故有a1+a3+a5+a7+a9+a11+a13+a15=392+a1；再考虑n分别为2,6,10,14 时,由a4+a2=5,a8+a6=17,a12+a10=29,a16+a14=41,得a2+a4+a6+a8+a10+a12+a14+a16=92.再数列{an}前16 项和为540,有(392+8a1)+92=540,解得a1=7.

追根索源1(2012年高考全国Ⅰ卷理科第16 题)数列{an}满足an+2+(-1)nan=2n-1,则{an}的前60 项和为____.

此外,2014年高考全国Ⅰ卷理科第17 题也有同工异曲之处.

题目4 第(1) 问解析设{an} 的公比为q,由题设得2a1=a2+a3,即2a1=a1q+a1q2.所以q2+q-2=0,解得q=1(舍去),q=-2.故{an}的公比为-2.

题目4 第(2)问解法一记Sn为{nan}的前n项和.由(1)及题设可得,an=(-2)n-1.所以

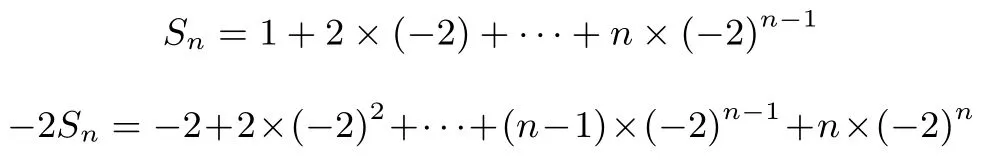
可得

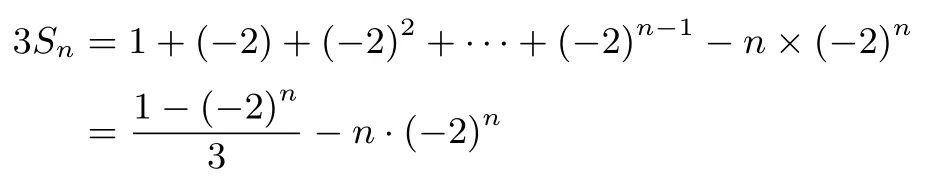
题目4 第(2)问解法二记Sn为{nan}的前n项和.由(1)及题设可得an=(-2)n-1,令nan=n(-2)n-1=(An+B)(-2)n-[A(n-1)+B](-2)n-1即n(-2)n-1=(-3An+A-3B)(-2)n-1.

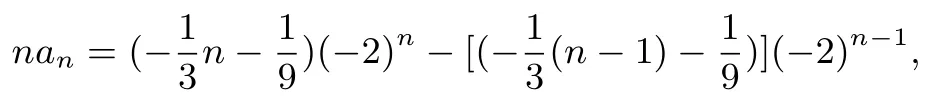
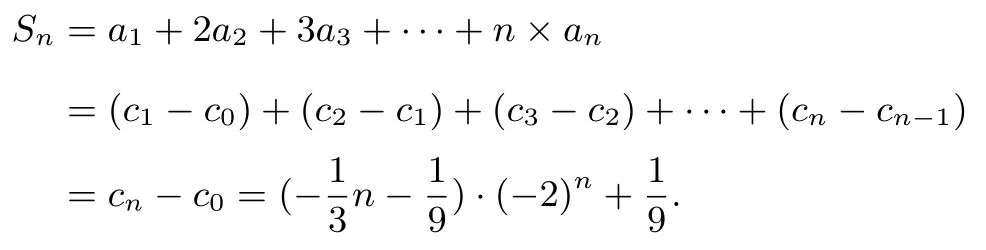
题目4 第(2)问解法三(导数)记Sn为{nan}的前n项和.则

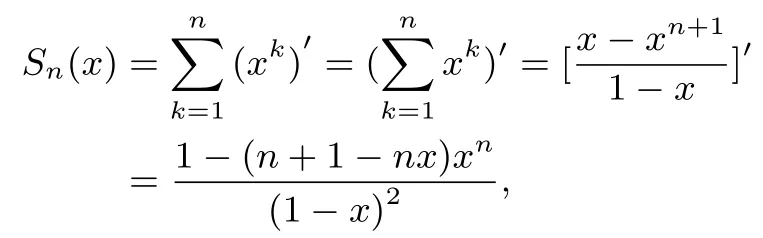
题目4 第(2)问解法四(分组)记Sn为{nan}的前n项和.由(1)知1,则有

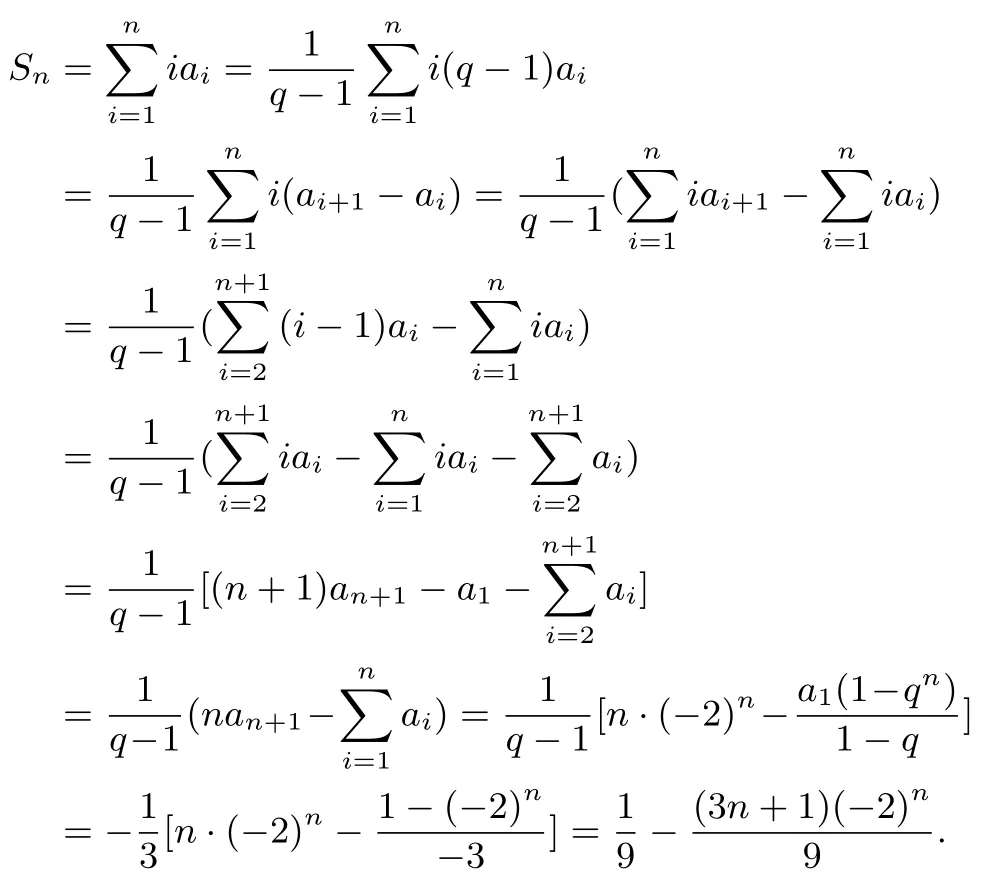
解法四的另一种表示由(1)及题设,得an=(-2)n,令Si=ai+ai+1+···+an,(i=1,2,3,···,n),则

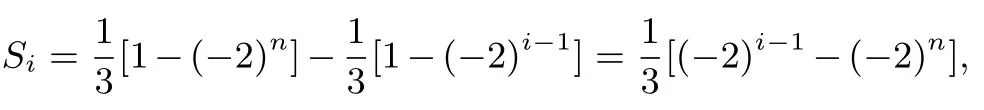
故

1.3 试题评析

1.3.1 数列知识考纲考查要求如下表

考查要求知识点及能力要求内容_________________________1.数列的概念和几种简单的表示方法(列表、图像、了解通项公式),数列的函数本质._____________________理解2.等差数列、等比数列的概念；___________________掌握3.等差数列、等比数列的通项公式和前n 项和公式4.能在具体的问题情景中识别数列的等差(等比)应用关系,并能用相关知识解决相应的问题____________

1.3.2 数列解题能力与考纲考查要求

考纲中明确规定高中数学学习要培养的数学能力是指：空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识.数列知识模块涉及到的数学能力主要有：①推理论证能力,②运算求解能力,③应用意识和创新意识.

1.3.3 数列解题思想方法与考纲考查要求

考纲中提出高中数学学习要具备的七大基本数学思想方法是指：函数与方程思想、数形结合思想、分类与整合思想、化归和转化思想、特殊与一股思想、有限与无限思想、或然与必然思想.数列知识模块涉及到的数学思想方法主要有：①函数与方程思想,②分类与整合思想,③化归和转化思想,④特殊与一般思想,⑤数形结合思想.

1.3.4 考题考查到的知识、能力、思想方法、核心素养如下表

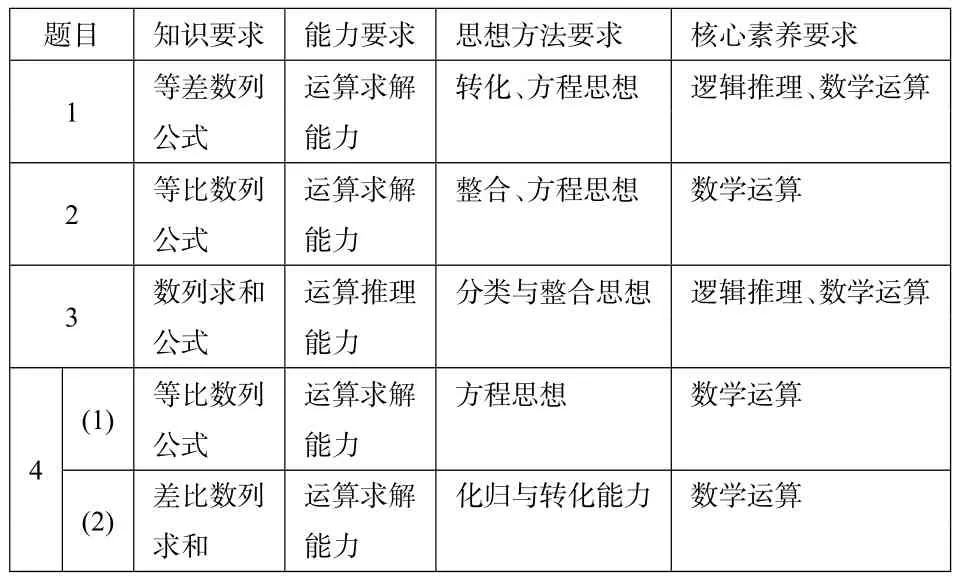
题目知识要求能力要求思想方法要求核心素养要求______等差数列运算求解转化、方程思想逻辑推理、数学运算1公式能力等比数列运算求解整合、方程思想数学运算2公式能力数列求和运算推理分类与整合思想逻辑推理、数学运算3公式能力等比数列运算求解方程思想数学运算(1)公式能力4(2)差比数列运算求解化归与转化能力数学运算求和能力

1.3.5 试题综述

今年文理科试卷在数列知识模块的考查中做到了统筹兼顾,展现了稳中有变,变中有新,新中有活的出题特点,坚持以能力立意,以知识为载体,落实核心素养,体现了选拔功能和区分度、对中学数学教学科学导向,从各个角度全面考查学生的数学素养.以下是我们收集整理的有关反馈.

关于全国文科Ⅰ卷的反馈注重基础概念、公式以及基本量的运算,善于从解题中利用整体的思想进行运算,提高运算效率,同时,也需要根据掌握的数列知识,进行分析,发现数列的规律,利用整体与局部思想,分析所需要的数据,从而进行问题的解决.

关于全国理科Ⅰ卷的反馈题型比较中规中矩,也是我们平时经常复习的题型,但是第二问入口较多,根据解法来看,可以从错位相减的基础方法,也可以从其他方法来解决,体现入口多的特点,符合筛选人才的作用.

关于全国文理科ⅠⅠ卷的反馈在对数列基础知识掌握的基础上,注重核心素养,侧重创新性的考查.设置了相应的生活情景作为数列的背景,考查学生观察、推理能力,并能利用数列来解决现实生活中的问题.

关于全国文理科ⅠⅠⅠ卷的反馈题型比较中规中矩,也是我们平时经常复习的题型,主要考查基本概念、公式和基本的运算.

关于新高考Ⅰ、ⅠⅠ卷反馈创新性体现较好,第一题是从两个等差数列发现公共项,并得到新等差数列的首项与公差,从而求解新数列的前n项和；第二题的第一问是等比数列的基本量运算,求通项公式；而山东卷的第二问是通过不等关系,找出新数列的特征,包含项数的计算,从而求出新数列的前n项和.在数列概念的理解上,从合并数列以及转化新数列,到公式、运算能力以及结合核心素养的考查,体现了“数列与函数”之间的本质联系.

综合今年各地高考试题,发现有以下特征：在抓好基础概念、公式,基本量的运算和方程的解法同时,值入直观观察、逻辑推理、优化计算、挖掘本质和文化素养等方面的能力和素养的考查,使得数列知识模块更具有新时代的气息.

今年,全国文理Ⅰ卷较以往有所不同,文理科考查的三角与数列的题型和位置进行了调换.今年,理科在原来考查解三角形的位置考查了数列,且只有1 道解答题,而文科在原来考查数列的位置考查了解三角形,并将考查数列的知识换成小题进行考查.

2 试题分析

2.1 典型错误详情参见参考文献[3],不再赘述.

2.2 考生答题情况错因分析

2.2.1 知识性错误概念不清,如题目4 中的第(1)问,误将等差中项表示成等比中项,如a12=a2·a3,或者自己编造公式,如2a1=a3-a2,不知道数列的表示方法,出现“数列an的公比为-2”的常识性错误,还有,利用第一问的结论来求第二问中数列{an}的通项时,将an=(-2)n-1写上成an=-2n-1.

2.2.2 能力性错误高考命题不光是凸显知识立意、能力立意,而且已经走向素养立意了,在试题中体现学科核心素养也是体现一道试题价值的核心指标.理科考生的思维能力普遍比较好,但是懒于动笔计算,很多时候,以为想通就会了.题目4 设置在理科,无论是第一问题解方程,还是第二问的底为负数的指数运算,都很好地考查考生运算能力.恰恰我们的考生,在答卷中呈现出因计算失误而失分的大有人在,主要表现为：一方面是没弄清楚等比数列的公比,一方面是在计算的过程中,将负号直接省略掉.

3 备考复习建议

3.1 考法研究,依纲靠本作为一线教师,要对高考方向有一个比较精准的判断和预测,除了研究高考试题,还要研究《课程标准》、《考试大纲》与《考试说明》.这三者是高考命题的指挥棒和重要依据,而2021年高考在没有《考试大纲》与《考试说明》的情况下,《课程标准》则更为重要,当然研究高考试题也要重要的标准之一,注意研究高考试题不局限某年某地,而是要放眼所有年份或省市的高考卷.通过研究高考试题,理清数列所考查到的知识要求,能力要求,把握所考题目难度,并根据考试大纲和课程标准进行分析,掌握在教学中,教师们需要把握的尺度,从所考查的题目来看,主要是考查数列的基本概念,等差等比数列的基本公式、性质,以及数列求和的常用方法,另外要注意隔项等差数列的考查.

3.2 教学建议

3.2.1 立足基础,关注概念公式的教学,注重知识生成,强化基础运算能力

在数列知识模块的教学或备考活动中,根据近几年数列知识模块的考查形势,我们教师要让学生理解数列的函数本质,数列的形成,等差等比数列公式的推导以及常见求和公式的推导过程,帮助学生清楚其来龙去脉,通过不断的变式和训练题来提升学生对公式的变形和形成的熟悉度；强化对数列一系列公式的记忆,促使学生明晰概念.特别,全国卷对数列基本量几乎每年都要考察,如今年的全国文科Ⅰ卷第10题,理科Ⅰ卷的17 题第一问,文理ⅠⅠ卷的第6 题,文科ⅠⅠⅠ卷第17 题第一问等,都考查基本量的运算,要求学生牢牢掌握住等差、等比数列基本量的关系方可解决问题,平时训练常用的通性通法即可.

3.2.2 强化训练,掌握数列性质特征,提升学生辨识能力

通过数列通项或求和公式对一个数列进行判断数列特征,才能为后面的解题提供思路和解题的后续,如全国ⅠⅠ卷理科题第6 题,通过观察,发现等比数列,并运用等比数列求和公式与指数方程解决问题.

掌握数列性质特征,有较好的辨识能力,则能简化解题思路,并且提高解题效率.如全国Ⅰ卷文科数列第10 题,学生若能掌握等比数列整体的思想,则可以提高答题的正确率,参照题目2 解析中的另解.

在高考备考中,老师可以通过各种题形式对学生进行针对训练,在题组训练中体验数列性质的灵活运用,加深对数列性质的理解,强化指对数的运算,提升学生的运算能力.

3.2.3 挖掘本质,培养学生转化、创新思维能力

增设生活、时代背景,学生需要在背景中提取数列的信息,才能进行数列运算.

如全国Ⅰ卷文科第8 题把程序框图巧妙与数列结合在一起；全国ⅠⅠ卷文科第3 题以钢琴为背景,考查数列中的列举能力；全国ⅠⅠ卷理科第4 题以天坛为背景,考查等差数列问题；还有山东、海南卷以数列为背景,研究新数列的特征.我们在平时教学训练的基础上,有针对性地选择相应题目,以培养学生的阅读能力以及转化能力.

纵观数列式题的命制,其考查内容离不开数列的本质,只是考查的形式和角度不一样.全国Ⅰ卷文科填空题16,以数列拆分与整合为背景,将从数列中分开奇偶项,在所列举的式子中找处规律,并从中做出选择,从而解决求和问题,学生只有掌握了整体和局部、转化化归的素养以及数列的本质,才能在解题过程中领悟和转化,达到解题的目标,具体参照题目3 解析.全国Ⅰ卷理科17 题第二问,以差比数列为背景,考生可以使用错位相减法、也可以使用分组求和,学生只有掌握了差比数列的本质,才能在解题过程中领悟和转化.具体参照题目4 解析.无论以任何形式进行考查,我们老师在平时教学中,要帮助学生理解好数列,并在训练中培养学生的创新能力.

综上,建议教师在高考复习备考中,做到强化基本概念、公式；训练学生的基本量运算和方程求解能力；突出性质的理解；培养学生辨识与转化能力；注重数列中的合二为一和一分为二的试题研究.