数学思想方法解决NOIP试题的探究

钟文耀

【摘要】  NOIP是一项全国性的信息学竞赛，其试题主要包含计算机编程和算法，运用数学思想方法可以帮助解答NOIP试题，其中数形结合是最重要的数学思想方法之一，运用数形结合分析和解决NOIP试题，可以为教学提供参考和借鉴。

【关键词】  数学思想方法 NOIP 数形结合

【中图分类号】  G633.6                      【文獻标识码】  A 【文章编号】  1992-7711（2020）25-139-02

一、研究背景

全国青少年信息学奥林匹克联赛（National Olympiad in Informatics in Provinces简称NOIP）吸引了全国众多中学生参与，NOIP分为普及组和提高组，普及组面向初中学生，提高组面向高中学生。二十多年，NOIP促进了计算机知识的普及和发展，为高校输送了许多有计算机特长的优秀学生，为社会培养了一批优秀的计算机人才。

近年来，学科知识竞赛逐渐被取消或被淡化，但学科知识竞赛对选拔优秀人才，促进学生综合素质的发展有特殊的作用。信息学竞赛是五大学科竞赛之一，相比其它学科的奥林匹克的竞赛，信息学竞赛参与的人数比较少，影响范围比较窄。NOIP的试题难度大、要求高，初学者往往对试题束手无策，这是因为解题需要选手掌握系统的计算机科学知识，拥有快速编程解题的综合能力，这对许多信息技术教师而言也是一项艰难的挑战。从NOIP试题分析入手，深挖解题方法，提高教学效率，对普及计算机科学有重要的意义和作用。

二、研究依据

NOIP考察选手掌握计算机科学的基础知识及编写程序解决问题的能力，其题目经常涉及一些数学知识，如奇数、偶数、素数、因子、最大公因数等，解题需要运用数学思想方法。NOIP试题以编写程序为主，程序设计的过程包括分析问题、建立数学模型、设计算法、编写程序、调试程序等五个步骤，其中建立数学模型就是重要的数学思想方法之一。建立数学模型的实质是对具体的问题进行抽象、近似和简化，使之表示成一些可以求解的数学公式，建立数学模型，才能确定算法，然后才能编写程序。

“数学思想方法”有侠义和广义之分，侠义的理解认为“数学思想方法研究的对象是数学本身的论证、运算以及应用的思想、方法和手段”，广义的理解认为“除了上述内容外，数学思想方法研究的对象还包括数学的对象、性质、特征、作用及其产生发展的规律”。中学数学包含着较多的数学思想方法，其中函数和方程、数形结合、配方法、图像法等，其中数形结合是最重要的数学思想方法之一。数形结合是根据数量与图形之间的对应关系，将抽象的数量与直观的图形相互转化，使复杂的问题具体化、形象化、简单化。

三、数形结合的运用

在数形结合的思想方法中，数包括数值、方程、函数、代数式和不等式，形包括图形、图表和图象。通过画数轴，或者建立平面直角坐标系建立数与形的对应关系，这是最常见的数形结合的运用。

1.单循环程序结构

循环结构的执行过程，可借助数轴来表示循环初值、终值和步长，例如for i=1 to 5 step 1（变量i从1到5的递增，每一步增加1）可以用图1的数轴表示。

2.简单双循环程序结构

在两重循环中，建立平面直角坐标系，将两个变量分别表示横坐标和纵坐标上的值，并描出对应的点，按数值变化过程连线和用箭头标明顺序，例如for i=1 to 4 for j=1 to 3（变量i从1到4递增，每一步增加1，同时变量j随i递增，j从1到3的递增，每一步增加1）可以用图2的坐标系表示。

3.复杂双循环程序结构

循环变量的初值或终值需要根据上一层循环变量的值来确定，例如for i=1 to 4 for j=i to 4（变量i从1到4，同时变量j从i到4）用图3的坐标系表示。

用数轴和直角坐标的图形来表示程序执行循环的过程，让抽象的程序变得直观和具体，可以加深了对程序执行过程的理解，对问题的解决提供了工具。

4、最短路径问题

数形结合的思想方法，不仅可以用在程序的循环分析中，也可以用在求最短路径的算法分析上。标号法是一种形象直观的求最短路径的算法，用数轴上的点表示图的顶点，用数值表示边的权值。

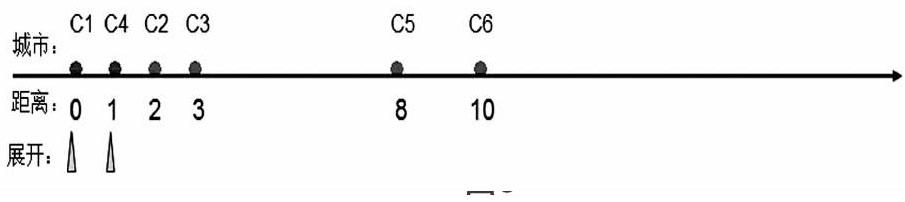
例1（NOIP2008普及组初赛）有6个城市，任何两个城市之间都有一条道路连接，6个城市两两之间的距离如下表所示，则城市1到城市6的最短距离为

分析：求最短路径的方法有很多，而标号法是一种非常直观的算法。在初中数学中，我们经常用数轴上的点来表示位置，用两点之间的距离是数轴上数值的差。这就是用到了数形结合的数学思想方法。同样我们也可以用一个数轴来表示城市，为了方便表示用C1、C2、C3、C4、C5、C6分别表示这6个城市，解题的过程如下：

（1）以城市1为0点，展开与其相邻的点，并在数轴中标出。

（2）因为C4离起点C1最近，再确定C4点为当前展开点，展开与C4想连的C2'、C3'、C5'和C6。

（3）由数轴可见，C3与C3'点相比，C3离原点近，因而保留C3，删除C3'，相应的，C2、C2'点保留C2点，C5、C5'保留C5，C6、C6'保留C6'，得到下图：

（4）此时再以离原点最近的未展开的C2，处理后，以此类推展开C3、C5，处理后得到最后结果：

由图可以得出结论：C4、C2、C3、C5、C6就是C1到它们的最短路径。这些路径不是经过了所有城市，而是只经过了其中的若干城市，而且到每一个城市的那条道路不一定相同，至于经过哪些城市，则可以记录上述过程。由此，可以知道C1到C6的最短距离为7。

总之，借助数形结合的方法可以分析和解决NOIP试题中的程序或算法问题，这是借助数学工具解决实际问题的运用，同时也是数学思想方法的运用。这有助于学生理解、分析、解决NOIP试题，为NOIP教学提供了借鉴和参考。

[ 参  考  文  献 ]

[1]方文祺.青少年信息学奥林匹克出击竞赛辅导（第二版）[M].天津：南开大学出版社，2007：1

[2]周全英，徐南昌.数学思想方法选讲[M].南京：南京大学出版社，1991：1

[3]顾建东.程序设计教学中的数学造[J].中学教学参考，2009.12：127