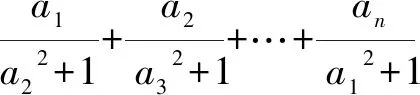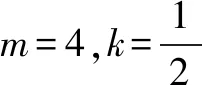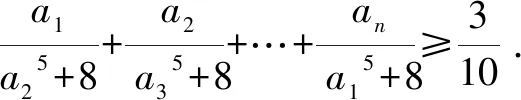对2017年美国数学奥林匹克压轴题的再推广

成克勤 庞耀辉

(甘肃省兰州市第七十一中学 730084)

一、题目再现及其推广

原题对满足a+b+c+d=4的非负实数a,b,c,d，

文献[1]给出上述问题的几个推广.

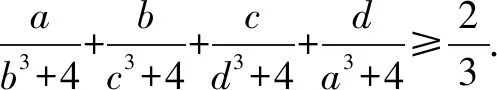
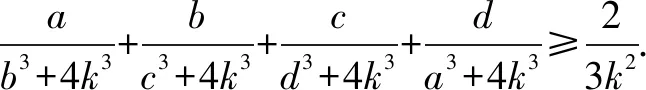
最后，给出更具一般性的命题及其证明.

命题如果非负实数a,b,c,d满足a+b+c+d=2nk,其中n为任意给定的正整数，k为任意给定的正实数，那么

二、联想再探究

上述结论是涉及四个非负实数的不等式，那么联想到：n个非负实数a1,a2,…,an(n≥4)之间是否存在相应的不等式呢？经探究得到如下结论.

定理如果非负实数a1,a1,…,an(n≥4)满足a1+a1+…+an=2mk, 其中m为任意给定的正整数,k为任意给定的正实数，

那么

下面我们先证明如下引理.

引理1若a1,a1,…,an≥0(n∈N,n≥4)，则4(a1a2+a2a3+…+ana1)≤(a1+a2+…+an)2.

证明设f(a1,a2,…,an)=4(a1a2+a2a3+…+ana1)-(a1+a2+…+an)2，

下面用数学归纳法证明f(a1,a2,…,an) ≤0.

当n=4时，f(a1,a2,…,an) ≤0

等价于4(a1+a3)(a2+a4)≤(a1+a2+a3+a4)2，由均值不等式知，命题成立.

假设当n=k(k≥4)时命题成立，

则当n=k+1时，不妨设ak=min{a1,a2,…,ak,ak+1},

于是有

f(a1,a2,…,ak+1)-f(a1,a2,…,ak-1,ak+ak+1)

=4[ak-1ak+akak+1+a1ak+1-ak-1(ak+ak+1)-(ak+ak+1)a1]

=-4[(ak-1-ak)ak+1+a1ak] ≤0,

故f(a1,a2,…,ak+1) ≤f(a1,a2,…ak-1,ak+ak+1) .

由归纳假设知

f(a1,a2,…,ak-1,ak+ak+1) ≤0，

则f(a1,a2,…,ak+1)≤0,

故当n=k+1时结论也成立.引理证毕.

引理2[1]对任意x≥0，都有xm+1-(m+1)kxm+mmkm+1≥0，当且仅当x=mk时等号成立(其中m为正整数，k为正实数).

根据引理2及x≥0可知，不等式x[xm+1-(m+1)kxm+mmkm+1]≥0成立，当且仅当x=0或x=mk时等号成立.

上述不等式等价于

(m+1)mmkm+2≥-(xm+1+mmkm+1)[x-(m+1)k],

从而有

其中当且仅当

a1=a2=mk,a3=a4=…=an时等号成立.

三、应用

根据这个定理，我们可以获得一些有趣的题目的解答或不等式.

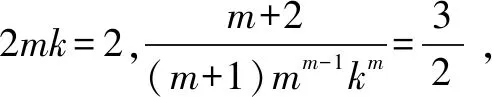
设整数n>3，非负实数a1,a2,…,an

满足a1+a2+…+an=2，