向量与条件交汇 破解与探究共存——2019年北京卷理第7题

汪浩淼

(安徽省马鞍山市和县第三中学 238200)

一、真题在线

A．充分而不必要条件 B．必要而不充分条件

C．充分必要条件 D．既不充分也不必要条件

本题把平面向量与充要条件的判断加以合理组合，以充要条件的判断为“脉”，同时以平面向量的夹角与模的大小关系为“络”，组成一个网络体系，加以合理逻辑推理及其应用．并在此基础上改变平面向量的夹角条件与模的大小关系加以进一步探究与拓展，深入理解与掌握，提升能力与素养．

二、真题解析

方法1：(余弦定理法)

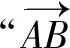
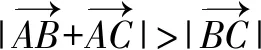
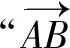
点评通过平面向量所对应的余弦定理法，根据充要条件的判断，从两个角度加以分类讨论，结合平面向量的线性运算与模的平方运算转化为平面向量的数量积的正负情况，与对应的平面向量的夹角情况对比，得以正确判断．

方法2：(平方转化法)

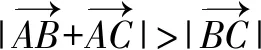
点评结合平面向量的线性运算，通过平面向量的模的平方运算加以等价转化，得以确定对应的平面向量的数量积的正负取值情况，结合平面向量的夹角的性质与数量积的关系，即可得以正确判断．

方法3：(平面几何法)

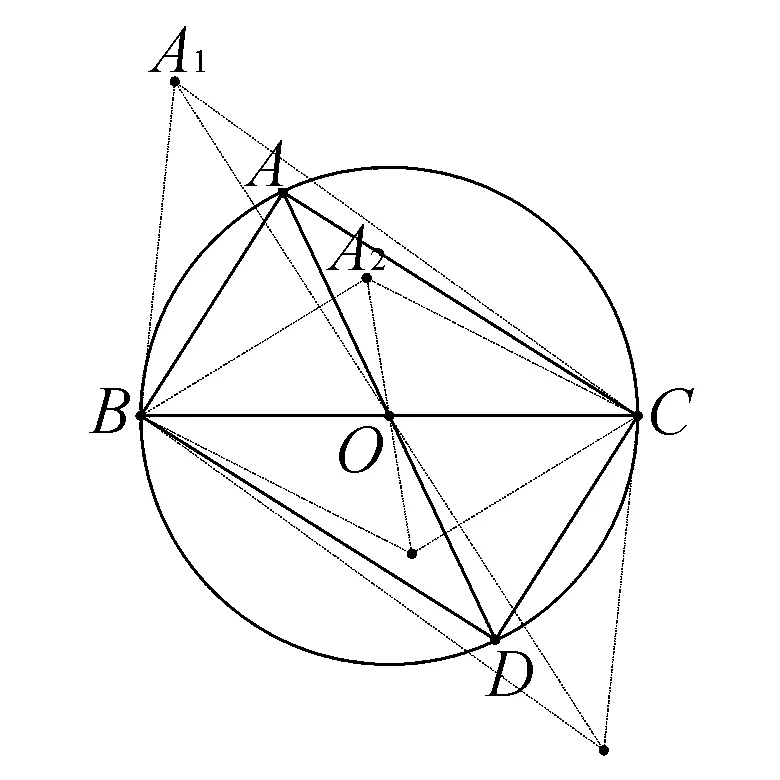
点评结合以BC为直径的圆O的直观图形，结合平面向量加法的几何意义以及圆的性质加以直观分类讨论，进而得以正确判断．从而也为点A在以BC为直径的圆O外、上、内三个不同的位置关系中以探究与拓展提供图形，进而得以有效类比与推广．

三、变式拓展

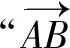
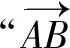
A．充分而不必要条件 B．必要而不充分条件

C．充分必要条件 D．既不充分也不必要条件

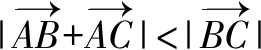
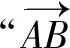
A．充分而不必要条件 B．必要而不充分条件

C．充分必要条件 D．既不充分也不必要条件

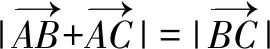
例题(2017·全国Ⅱ文·4)设非零向量a，b满足|a+b|=|a-b|，则( ).

A．a⊥bB．|a|=|b| C．a∥bD．|a|>|b|

解析由|a+b|=|a-b|可得|a+b|2=|a-b|2，则有a2+b2+2a·b=a2+b2-2a·b，即4a·b=0，则有a⊥b，故选择答案：A．

四、规律总结

涉及平面向量的夹角问题，特别与之对应的平面向量的数量积的正负取值问题，还要注意两平面向量平行的情况，当中涉及两平面向量方向相同与方向相反问题，对应夹角为零角与平角．特殊在一些夹角的判断的求解过程中，容易出现遗漏或混淆而导致错误，要引起高度的重视．