中学的方法解决特殊二次不定方程

罗嘉隽

(福建省三明市梅列区洋溪中学 365000)

不定方程一般来讲，我们只能给出不定方程的求解的思路方法，利用数学方法技巧，目的要将不定方程转化成已解决的结果的方程.这就要求需要相当熟练的初等和高等的数学知识，才可以在不定方程中研究出有价值的结果.但是，这不是绝对的，在初等的证明中，具有熟练的初等数论基础知识也会能得到好的成果.二次不定方程与我们中学数学学习联系，可以用一些中学学习的知识，解决几类二次不定方程.

一、形如x1+x2+x3+…+xn=y2二次不定方程的整数解

二次不定方程有很多特殊的类型，对于特殊类型我们可以方便地研究出一些好的性质，其实在中学我们接触到的不定方程主要是一次不定方程，二次不定方程较少.中学我们学习了数列，其中数列an=2n-1(n∈Z+)对数列求和，发现可以构造出一类二次不定方程，而且这类不定方程的整数解有一定规律.发现奇数数列是此类不定方程的整数解.

1=12

1+3=22

1+3+5=32

1+3+5+7=42

………………………

1+3+5+7+…+(2n-1)=n2(n∈Z+)

证明1,3，5，7，…，2n-1，…是等差数列，

an=2n-1(n∈Z+).

发现奇数列求和时右边出现了二次项，如果把奇数列换成未知数，二次项换为未知数，由此启发归纳一种类型的二次不定方程，形如x1+x2+x3+…+xn=y2.其中要求x1，x2，x3，…,xn，都不为零，因为若其中一个为零那么方程的左边就相当于少一个元变为n-1个元形式.

x=y2，

有整数解x=1，y=1;

x1+x2=y2，

有整数解x1=1，x2=3，y=2;

x1+x2+x3=y2，

有整数解x1=1，x2=3，x3=5，y=3;

……

x1+x2+x3+…+xn=y2，

有整数解x1=1，x2=3，x3=5，…，xn=2n-1(n∈Z+)，y=n.

显然零解也满足方程.

此类不定方程的形式为x1+x2+x3+…+xn=y2(n∈Z+)，奇数列是此类不定方程的一个解x1=1，x2=3，x3=5，…,xn=2n-1，y=n是方程的整数解.

例1求方程x1+x2+x3+x4+x5+x6=y2

(x1，x2，x3，…，x6，y,都不为零)的整数解.

解方程左边有6项，满足这样形式的整数解可以看做6项an=2n-1的数列求和，则x1=1,x2=3,x3=5,x4=7,x5=9,x6=11,y=6是满足方程的整数解.

由于等差数列的求和公式出现了二次项，那么我们将此结果一般化的话，只要是一个等差数列的每一项是整数，那么通过求和公式构造出一类二次不定方程，那么这个整数列的等差数列，是此类不定方程的整数解.

等差数列的通项公式an=a1+(n-1)d(n∈Z+)，当a1和d是整数，那么这个等差数列是整数列.

其中整数列an=a1+(n-1)d(n∈Z+)，y=n是不定方程的整数解.

(其中x1，x2，x3，x4,x5,y，都不为0).

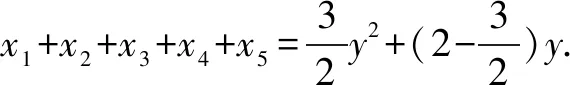
左边有5项，满足这样形式的整数解，可以看成是a1=2，d=3.

an=2+(n-1)3的前5项求和，n=5，则x1=2,x2=5,x3=8,x4=11,x5=14,y=5是方程的整数解.

二、余弦定理形式的不定方程

中学还接触到了余弦定理，那么当三角形ABC三边为未知数，形如余弦定理形式的二次不定方程整数解，可以把问题转而寻找满足方程整数边的的三角形.

如果三角形ABC的三条边分别a，b，c，当a，b，c为整数时，那么形如

a2+b2-c2-2abcosC=0

的方程有整数解ma,mb,mc.

例3三角形ABC的三边分别为a=2，b=4，c=5，

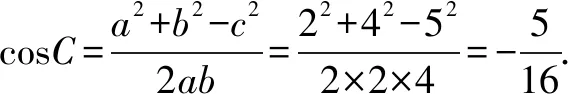
当二次不定方程在有几何意义下，如满足余弦定理的形式a2+b2-c2-2abcosC=0(-1≤cosC≤1).

那么满足这样情况的不定方程，可以结合余弦定理的几何意义来找不定方程的整数解.

三、形如ax2+bxy=c(a,b,c∈Z+)二次不定方程的整数解

形如ax2+bxy=c可以观察到方程的左边可以进行因式分解，将方程的左边转化为两因式相乘的形式，简化二次不定方程，具体参见以下例题.

例4求方程x2-xy=5的整数解.

解将方程进行因式分解x(x-y)=5,

x,y∈Z+，x，x-y是5的约数.

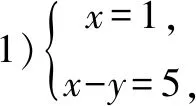
本文到此，构造一类等差数列求和形式的二次不定方程，联系中学学习的等差数列进行结合，找出此类二次不定方程特殊的整数解，由余弦定理的形式构造了有几何意义的一类二次不定方程.

二次不定方程是研究不定方程的入门，联系中学接触的一些知识，对启发人们对不定方程的兴趣有着一定的作用，对研究高次不定方程有着过度借鉴的作用，与中学的等差数列和余弦定理相联系，能够使中学生引起兴趣.不定方程研究是数论中的一个难点，但不定方程的形式简单易懂，内容丰富方法多样，研究不定方程，对人们智慧是一个挑战，探索数学深处奥秘的一步.学习不定方程能够锻炼数学思维与逻辑能力，拓展数学知识面，提高数学分析能力与解决问题能力.