高职数学教学中融入教育元素的实践与研究——以极限概念教学为例

王咏芳

(苏州健雄职业技术学院，江苏 太仓 215411)

1 极限概念的引入

引例1：庄子(前369年—前286年，战国)曾写道：“一尺之棰，日取其半，万世不竭。”当n越来越大时，棰越来越短，逐渐趋于0，这里从直观上体现了极限思想。

引例2：刘徽(约公元225-295年，魏晋时代人)创造了用“割圆术”来计算圆周率的方法，从而开创了我国数学发展中圆周率研究的新纪元。他从圆内接正六边形算起，依次将边数加倍，以致算到内接正3 072边形的面积，从而得到圆周率π的近似值3.1416，后人为了纪念刘徽，称这个数值为“徽率”。这里他已经把极限的思想应用于近似计算，这种方法比欧洲早了1 000多年。

利用两个引例，以数学文化为背景，借助科学家们的真实事迹，引导学生要善于观察，善于思考，善于总结。

2 极限概念的分析与解读

2.1 数列极限

数列极限的(描述性)定义：在数列{xn}中，如果当n无限增大时，xn无限地接近于确定的常数a，则称当n趋向于无穷大时，数列{xn}的极限为a，也叫做数列收敛于a；否则就称数列是发散的。

解读1 “n无限增大”：就是要求数列必须是无穷数列，也就是说极限问题中的数列必须是无穷数列。

解读2 “确定的常数a”：是指唯一的常数，而后面的“否则”是指a的不唯一或不确定。

解读3 数列的极限只有收敛或发散，二者只居其一也必居其一。发散的数列也可以叫做不收敛的、没有极限的，还可以叫做数列极限不存在。

解读4 “无限地接近于”、“趋向(于)”：这是两个相同意义的文字描述，也是描述性定义的缺陷和不精准所在。用下面两个收敛数列解说：

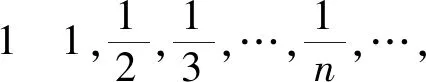
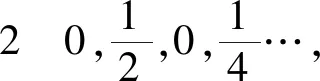
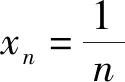
解读5 既然是总体的变化趋势，那么数列的前有限项的变化：变项值、去除、添加等，对数列的极限不产生影响，即可以有下面的定理：

定理 数列中去除、添加有限项后的新数列，其敛散性不变。

试想一下：{xn}与{kxn}(k≠0)的敛散性有变化吗？

解读6 数列的无穷多项的变化，将导致敛散性发生变化。

数列3a,a,a,…；

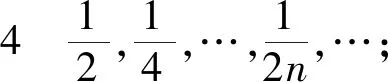
当a=0时，数列3和数列4是数列2的两个子数列，分别为奇数项子数列和偶数项子数列，也可以说是数列2去除无穷多项后的数列，因为数列2是收敛的，所以数列3和数列4都是收敛的。

当a=2时，数列3和数列4仍都是收敛的，若仍分别为奇数项子数列和偶数项子数列，则原数列是发散的。

2.2 函数极限

2.2.1 当x→∞时的情形

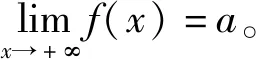
类似地，可定义函数f(x)在x→-∞时或在x→∞时的极限。

解读1 在描述性定义中，自变量趋于无穷(x→∞)时的函数极限与数列极限是相似的，主要区别是：函数中自变量可以不是正整数，是实数范围；自变量的变化不要求单调的。

解读2 记号“x→∞”称为“x趋向于无穷(大)”，而实际上它细分为3种情形：x取正值无限增大，记作x→+∞，称为“趋向于正无穷”；x取负值而无限增大，记作x→-∞，称为“趋向于负无穷”；x可取正值也可取负值，而|x|无限增大，记作x→∞，称为“趋向于无穷”。

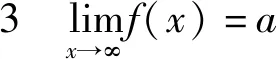
2.2.2 当x→x0时的情形

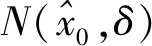
解读1 自变量趋向于有限数(x→x0)是指自变量x并不要求等于(取到)x0，即：函数值f(x0)的有无或大小并不影响极限存在与否。

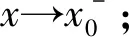
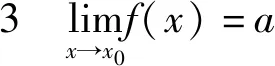
3 极限符号的书写

总之，极限的概念是有众多可以推敲的地方，是体现数学思想的场所，是引导学生学会发现问题、分析问题、解决问题的练兵场。在教学过程中恰到好处地融入一些教育元素，使学科教育与思政教育做到和谐统一，更好地实现既教书又育人。