HPM视角下弧度制概念的教学设计

黄 春 石子璇

(扬州大学数学科学学院,225002)

弧度制的本质是用线段的长度来度量角的大小. 弧度的引入, 实现了度量的统一, 这样，三角函数的自变量和函数值就可以进行运算, 基本初等函数的四则运算、符号运算和求反函数等便于实现, 使得函数具有更广泛的应用性. 本文介绍如何利用数学史料和生活实例, 在双层空间的框架下进行弧度制概念的教学设计.

一、弧度制知识空间设计

对于弧度内容的教学设计, 教学活动与知识空间的设计, 强调符合学生认知发展规律以及知识内在逻辑体系. 依据课程安排, 学生已有的知识仅有任意角, 对于弧度, 可以说是全新的. 《普通高中数学课程标准》对于“任意角与弧度制”这一节的目标设定为:了解任意角的概念和弧度制, 能进行弧度与角度的互化. 而弧度制实质上是将角与实数联系起来, 在弧度制的基础上, 与扇形相关的计算公式变得更为简便, 学习扇形的弧长与面积公式也是本节课的一大重点. 根据上述知识目标, 本节知识结构设计如图1.

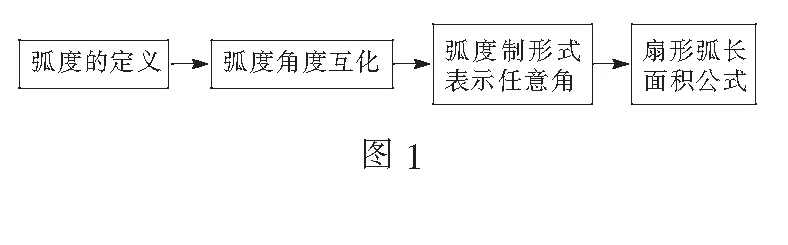
设计说明在实际教学中,多数教师往往只关注弧度制与角度制的互化,而重视弧度定义的教学活动,更有利于使学生明了学习弧度制的重要意义.

二、 教学活动设计

学习活动有四种形式:相关史料的数学阅读类, 记作AR(read);基于问题的学习连续统, 记作AP(problem);知识主题的探究式学习, 记作AC(cause、explore);巩固知识的解题实践, 记作AE(exercise)等. 同时, 弧度制包含十分丰富的历史文化内涵, 基于HPM教学方式与双层空间教学理论, 选取教学活动如下:

1.相关史料的数学阅读类(AR)活动

AR 1 了解弧度制的萌芽,阅读阿波罗尼奥斯偏心轮模型, 了解最初的两种弦表:希帕克斯弦表, 托勒密《大成》中的弦表.

设计说明弧度制的发展是依托三角学和角的发展的,偏心轮模型最早应用于天文学解释四季不等长的现象.由此而产生的弦表虽然与现在的三角函数存在区别,但已经初步显示三角函数实质上为弧与弦之间的关系.让学生明确在给定半径时,弧长与角度的一一对应关系.从历史上看,弧长在当时也使用60进制,显然为了避免进制带来的运算麻烦,引入弧度制是必然的.

AR 2 数学史上三角学与弧度制的形成:利提克斯在直角三角形中定义正弦、余弦、正切、余切、正割和余割;欧拉在《无穷小分析引论》中给定圆的半径为单位来度量弧长.

设计说明弧度制传播与确立的历史阅读,实质上是感受弧度制意义的学习过程.在弧度制传播的历史过程中认识到弧度制不断地进步与发展,从而达到广泛应用的地位,暗示弧度制是进行三角学学习的基础知识.

AR 3 《数学名词》一书中最初将“radian”翻译成弪(jing), 取自弧与径二字. 直到1956年新版的《数学名词》才弃用“弪”, 将“radian”译为“弧度”.

设计说明新课标中明确指出“弧度是学生比较难接受的概念”. “弪”字的使用从字形上就已体现了弧度是由弧长与半径决定的. 学生阅读弧度制命名的由来, 不仅能感受中国数学文化中弧度的由来与发展, 也能加深对弧度制的印象与理解.

AR 4 案例阅读. 请查阅文献[5], 感受弧度制的意义.

设计说明角度制到弧度制的转变，实际上是三角函数中自变量由弧长到角的转变.了解弧度制产生的缘由与意义,也是明晰弧度制在三角函数知识框架中的地位的过程.更甚者,在文献[5]中, 提及了弧度制对于三角学发展的重要意义, 也是学生探索高等数学中微积分、级数知识的基础.

AR 5 案例阅读. 查阅文献[6], 认识角的度量的多种进制.

设计说明拓宽学生的思路,在文献[6]中, 介绍了弧度制在使用上的多种变形, 如运用于科学研究的毫弧度, 运用于军事的密位制, 法国人广泛使用的百分制…不仅是让学生认识到度量角的多种进制, 也是让学生了解弧度制的多种应用, 感受其重要意义.

2.基于问题的学习连续统(AP)类活动

AP 1 介绍我国古代著名数学家祖冲之的伟大成就, 以其重要发现“圆周率”引入, 提问:一般情况下, 当圆心角确定时, 圆心角所对弧长与半径之比是否为与半径无关的常数?(并通过计算:“给定角度为30°,60°的圆心角, 当半径r=1, 2, 3, 4时, 分别计算对应的弧长l, 再计算弧长与半径的比.”验证猜想)

设计说明圆周率表明在圆中周长与半径之比是与半径无关的常数.由此类比,学生自然猜想在一般情况下也成立,再进行验证计算，更加能够使学生接受这点,而不至于突兀.同时也在其中渗透了数学历史文化的学习.

AP 2 具体问题解答.

设计说明用角度制计算弧长,不仅是对角度制的复习巩固,也为弧度与角度互化公式的学习搭建桥梁.有利于学生利用已有的认知结构同化新知.同时,弧长的计算方式,也为比较弧度制与角度制奠定基础.

AP 3 总结1°=______rad, 1 rad=______°.

请计算一些特殊角的弧度数(略).

设计说明学生自己动手计算弧度与角度之间的换算,明晰弧度制与角度制之间的关系,感受弧度制与角度制各自的优势,加深对弧度制的理解，提高学生的逻辑思维能力,从抽象中感受具体,拓宽思路.

3.知识主题的探究式学习(AC)类活动

AC 1 比较sinα与α的大小并举例说明.

设计说明正弦值为实数,两者比较,则角也需为实数.让学生在问题中意识到运用弧度制的必要性,并且能够将角度制化为弧度制.

AC 2 思考：是否弧度制的划分方式比角度制更合理?

AC 3 学习弧度与角度互化后, 讨论问题:

问题1 弧度制与角度制最本质的区别是?

问题2 弧度制与角度制各自的优势如何体现?

设计说明坚持以学生为主体的教学观,让学生通过新旧知识的比较分析,将所学的内容内化到已有的知识体系.

AC 4 请建立角集合与实数集的对应关系.

设计说明让学生在探索过程中，直观地感受到，如何借助弧度制实现角与实数的一一对应.

AC 5 学习了弧度制, 在已有的角度制下的扇形弧长、面积公式的知识基础上, 讨论问题:

问题1 弧度制下扇形弧长公式.

问题2 弧度制下扇形面积公式.

设计说明将计算得出的弧度制下扇形的弧长与面积公式与角度制下的公式比较,学生能够快速地认识到弧度制为计算带来的便利,学生很容易接受学习弧度制的缘由.

4.巩固知识的解题实践(AE)类活动

AE 1 时钟经过5分钟, 分针与秒针各转过多少弧度?

AE 3 将-1480°写成α+2kπ(k∈Ζ)的形式, 其中0≤α<2π.

AE 4 如图3, 求火车轨道拐道处弧AB的长(忽略轨道宽度), 其中∠AOB=60°.

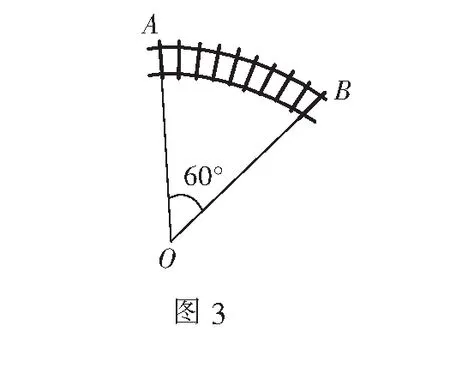
AE 5 已知扇形的周长为30 cm, 当它的半径和圆心角各取什么值时, 才能使扇形的面积最大?最大面积是多少?

运用上述教学活动, 构成双层空间(如图4):

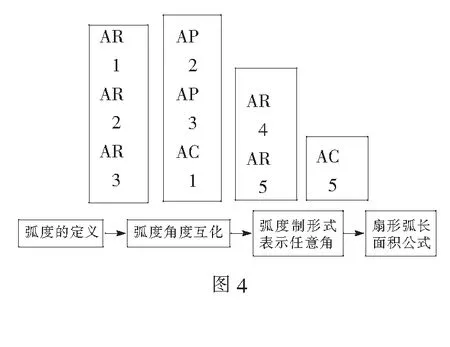
设计说明在双层空间的教学原理上,配合各种教学活动,在弧度制的概念与应用中,再现弧度制的产生过程，符合学生的认知规律,帮助学生建立完整的知识网络,通过经历蕴含数学史的教学活动,感受数学文化的深度.