太阳能塔气弹模型结构优化研究

李寿英，孙北松，刘 敏

(湖南大学风工程与桥梁工程湖南省重点实验室，湖南 长沙, 410082)

太阳能光热电站的吸热塔是一种典型的高耸结构物，它通过吸收周围定日镜所反射的太阳光能进行发电[1]，其外形与烟囱相似，通常为圆柱状，但二者内部结构完全不同。因气动阻尼的影响，高耸结构易在临界风速下发生大振幅涡激振动[2-5]，吸热塔的Strouhal数(St)约为0.2[6]，其与第1阶模态相关的涡激振动临界风速通常低于结构设计风速。与其它高层建筑相比，混凝土吸热塔的塔身连接节点和内部的设备较少，结构阻尼比更小，对于风的作用也更为敏感[5，7-9]。针对这种新型的结构体系，目前尚无专门的设计规范，通常只能参照烟囱的设计规范进行设计，且需借助风洞试验展开相关的振动控制研究。

常用的高层建筑风洞试验方法主要有刚体测压模型、弹性支撑刚性结构的单自由度及多自由度气弹模型等[10]，其中仅多自由度气弹模型能全面真实地反映风与结构的相互作用[11-13]。多自由度气弹模型的刚度模拟通常有3种方法：直接模拟几何外形和刚度的离散刚度法[14]、采用芯梁模拟刚度的集中刚度法[15]以及刚性节段加弹簧连接件法[16]，其中离散刚度法与集中刚度法都能成功模拟相应模型连续的刚度变化，但前者对模型的加工精度要求较高。本课题组针对太阳能塔的几何和物理特性，设计出一种可反映实验对象全部振动特性的多自由度气弹模型[8-9]，该模型在摩洛哥Noor III电站的风振试验研究中取得了良好的模拟效果，但模型外衣较薄(0.8 mm)，难以加工且易变形，导致结构阻尼比调节困难，有鉴于此，本文基于该气弹模型设计方法[8]，以某光热电站的太阳能塔结构为研究对象，通过对其模型结构进行优化，设计并制作了适用性更强的太阳能塔气弹模型。

1 研究对象

研究对象为某光热电站太阳能塔，如图1所示，以地面处为太阳能塔底面，塔身高度243 m，其中从底面至200 m高度范围内为圆形变截面钢筋混凝土结构，混凝土标号包括C50、C40、C35，该部分结构详细尺寸变化见表1；钢筋混凝土结构上方即塔身200～243 m高度范围内为钢结构集热筒，二者之间借助牛腿(塔身200 m处)相连。钢结构集热筒材质为Q235工字钢，外径为16.00 m，其外表面悬挂太阳能吸热板，吸热板外径为20.00 m。混凝土塔身及集热筒中布置有多个工作平台，为塔身提供横向支撑。

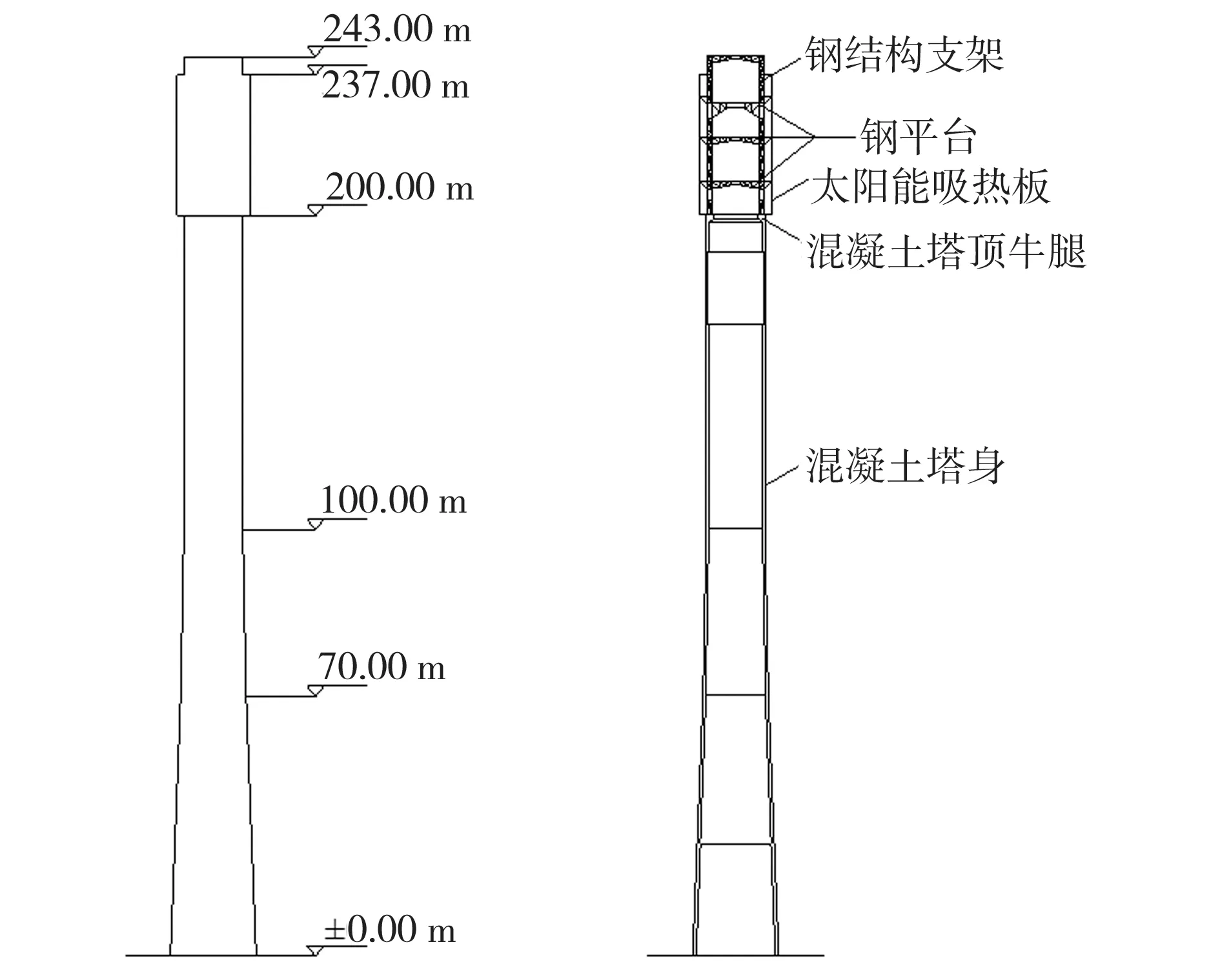
(a)太阳能塔外立面图 (b)竖向结构布置图

(c)集热筒平面布置图 (d)塔身截面布置图图1 太阳能塔结构布置图Fig.1 Structural arrangement of the solar tower

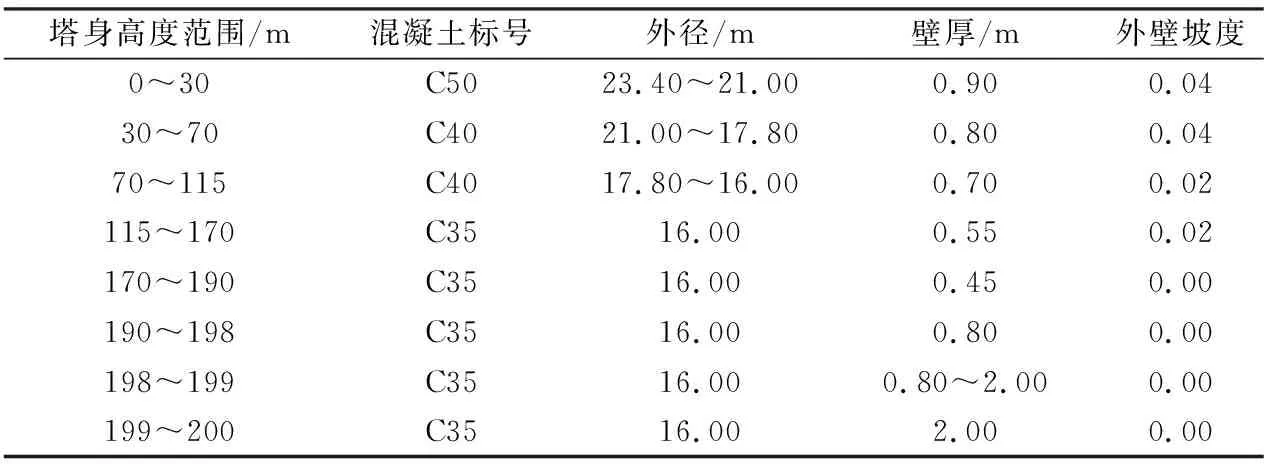
表1 混凝土塔身主要尺寸Table 1 Key dimensions of the concrete tower body

2 模型设计与优化

2.1 原型结构动力特性

采用ANSYS软件平台建立原型结构的三维有限元模型，并对其进行动力特性分析以确定模型设计的目标结构参数如振型和频率等。钢筋混凝土塔身部分采用BEAM188单元模拟，塔底与基础为完全刚性连接；忽略钢筋混凝土塔身内部工作平台及楼梯的刚度，采用MASS21单元进行配重；采用BEAM188单元模拟集热筒的钢结构杆件，节点为刚性连接；太阳能吸热板悬挂于集热筒外部，不提供刚度，采用MASS21单元进行配重；集热筒钢结构杆件伸入混凝土塔身的牛腿部分锚固，可考虑为刚性连接，采用刚臂MPC184单元使钢结构底部与混凝土塔身顶部的位移和转角协调。图2所示为该太阳能塔前3阶模态的振型图，相应的频率依次为0.27、1.07、2.04 Hz。

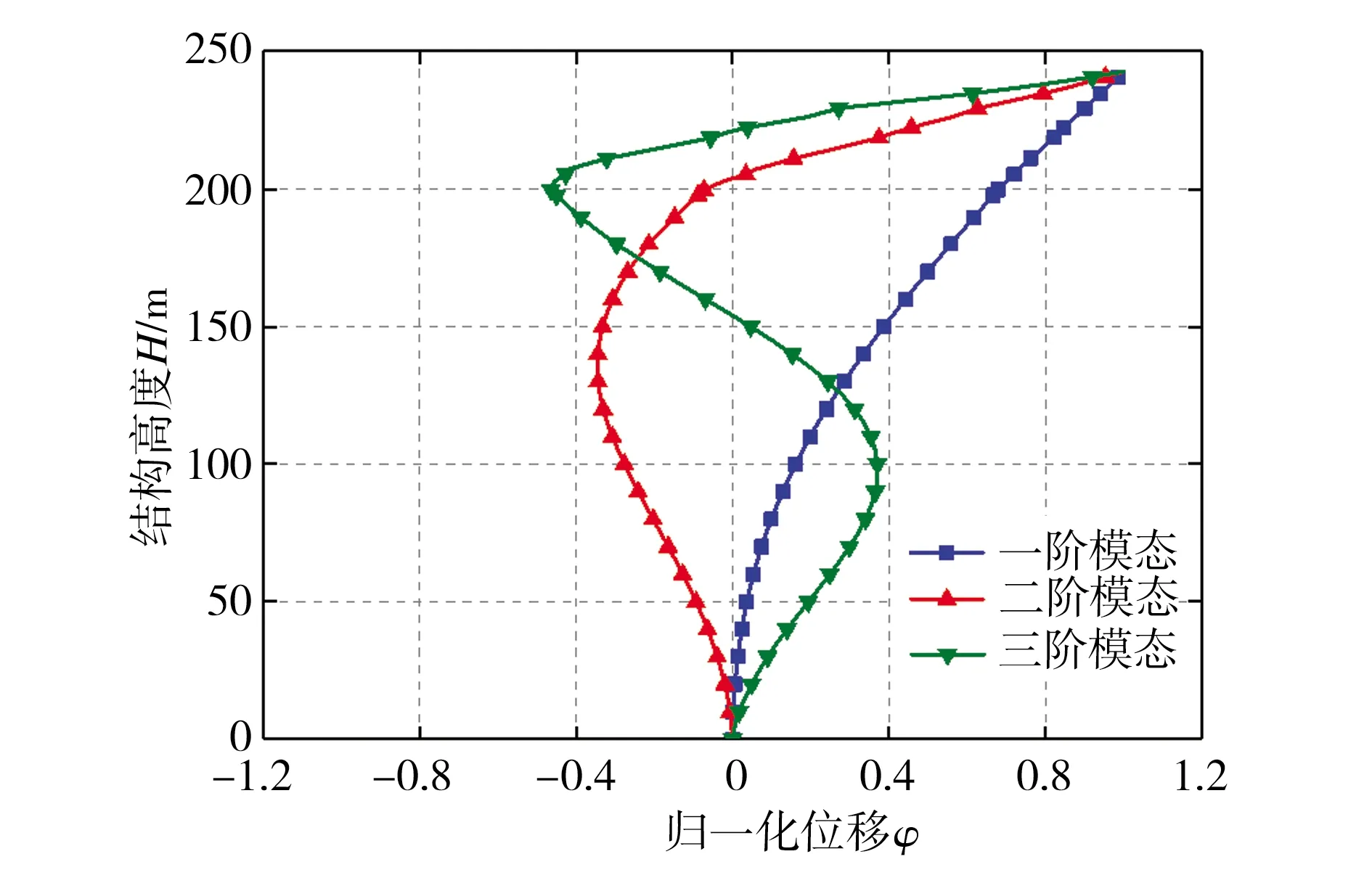
图2 原型结构前3阶模态振型Fig.2 The first three mode shapes of the prototype structure

2.2 气弹模型设计

在忽略Reynolds数和Froud数的情况下，初步拟定气弹模型几何缩尺比为1∶200，风速比为1∶5，表2列出了主要物理量的相似比关系，其中n为几何缩尺比，m为风速比，由此可以推导出该结构前3阶模态的目标频率依次为10.64、42.84、81.52 Hz。

表2 气弹模型相似比Table 2 Similarity ratio of aeroelastic model

模型设计中本应保证模型结构刚度、质量分布与原型结构严格相似，但若采用与原型结构完全相同的结构形式，则结构壁厚较薄，不利于结构稳定及加工精度的控制，故本研究采用集中刚度法，将原型结构的刚度借助某一模型构件进行单独模拟，以便于控制模型制作精度。图3所示为模型详细设计方案，模型主材选择质地较轻且易加工的铝合金,在混凝土塔身部分设置通长的芯梁来模拟结构刚度，以保证结构刚度连续、精确。混凝土塔身的模型由底座、芯梁、圆盘、外衣和螺丝5个部分组成，其中芯梁提供弯曲刚度，外衣保证气动外形及质量分布相似，圆盘和螺丝连接芯梁和外衣，底座与天平相连以测量基底力。芯梁、圆盘和底座均由实心铝合金圆柱一体化机加工。外衣分为六段，相邻外衣之间缝隙为2 mm。集热筒钢结构部分采用杯状结构模拟，以预留出模型中安装减振装置的空间，芯梁顶部和集热筒底部采用螺丝连接。采用铜条作为配重，粘贴在相应高度的外衣内壁上。

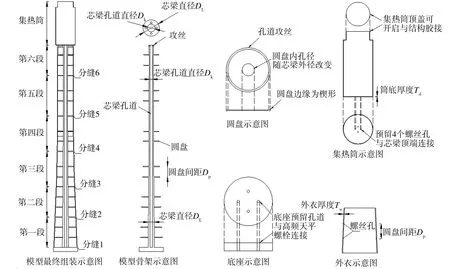
图3 模型设计方案Fig.3 Project of model design

2.3 模型结构的有限元模型及动力特性分析

在进行模型加工之前，先基于ANSYS软件平台建立模型的有限元模型如图4所示，通过分析其动力特性并与目标值比较，以判断模型设计的合理性。其中，芯梁采用BEAM188单元模拟，圆盘、外衣和集热筒杯状结构均为薄壁结构，借助SHELL63单元进行模拟，由于芯梁与圆盘为一体化加工，它们之间为完全刚性连接，通过设置主、从节点实现模拟，外衣与圆盘之间、芯梁顶部与集热筒杯状结构底部之间也为完全刚性连接，采用MASS21单元模拟配重，模型底座处的边界条件采用完全固结形式。模型虽与实际结构的构造不同，但其结构参数需满足表2所示的相似比关系。对该有限元模型进行动力特性分析时，在质量比严格满足相似比关系的情况下，频率比也要满足表2要求，且振型与实际结构相同，此外，芯梁内径Dk、圆盘间距Dp及集热筒杯状结构底部厚度Td等3个参数对模型动力特性影响较大，因此可通过调整上述参数来优化太阳能塔气弹模型结构。

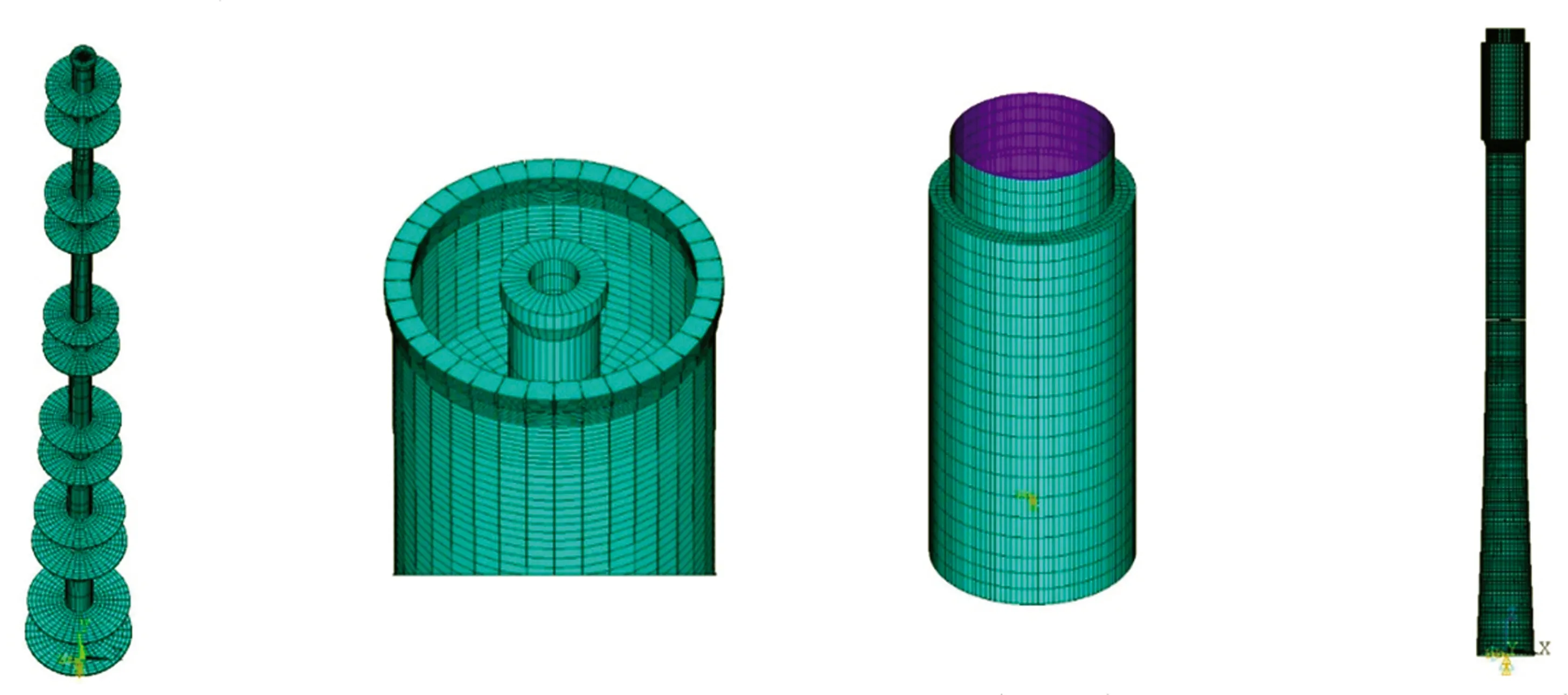
(a)芯梁与圆盘 (b)芯梁顶部 (c)集热筒 (d)全塔模型图4 基于ANSYS的太阳能塔模型有限元模型Fig.4 Finite element model of solar tower model obtained from ANSYS

2.4 气弹模型结构优化

2.4.1 芯梁内径Dk的优化

芯梁设计成圆环形截面的同时需保持其弯曲惯性矩与原型结构严格相似，从而对模型结构的振型和频率不产生影响，对芯梁内径Dk的优化目标是降低模型的加工难度。在保持结构质量及芯梁抗弯刚度不变的条件下，塔身不同高度截面处的芯梁壁厚TL及外衣壁厚Tw随芯梁内径Dk的变化规律如图5所示。由图5(a)可见，塔身不同高度截面处的TL均先随着Dk的增大而减小，最后逐渐趋于定值。这是因为在塔身截面面积相同的条件下，芯梁外径的增大会引起结构弯曲刚度显著增大，为保持弯曲惯性矩不变，必须减小芯梁壁厚，但当Dk超过35.00 mm以后，TL已不再发生明显变化，且此时TL最小值(塔身180.00 m截面处)已经小于1.00 mm，给模型加工造成了很大的困难，不便于芯梁与集热筒杯状结构的连接，还将导致模型结构不稳定。从图5(b)中可以看出，塔身不同高度截面处的Tw均先随着Dk的增大而增大，最后逐渐趋于稳定值。其中当Dk大于10.00 mm时，Tw最小值(塔身180.00 m截面处)仍大于1.00 mm，满足加工的条件限制，此外，当Dk介于10.00～ 30.00 mm时，Tw变化最为剧烈，这是因为在保持刚度相似的同时还应保持质量分布的相似，增大芯梁内径减小了芯梁的质量，将更多的质量分摊到外衣中，造成外衣厚度Tw显著增加。综合以上分析可得，增加芯梁内径Dk可以显著减小芯梁质量，增加外衣厚度，减小模型结构的扭转效应与加工难度，故结合实际加工条件，选定芯梁内径Dk为12.70 mm。

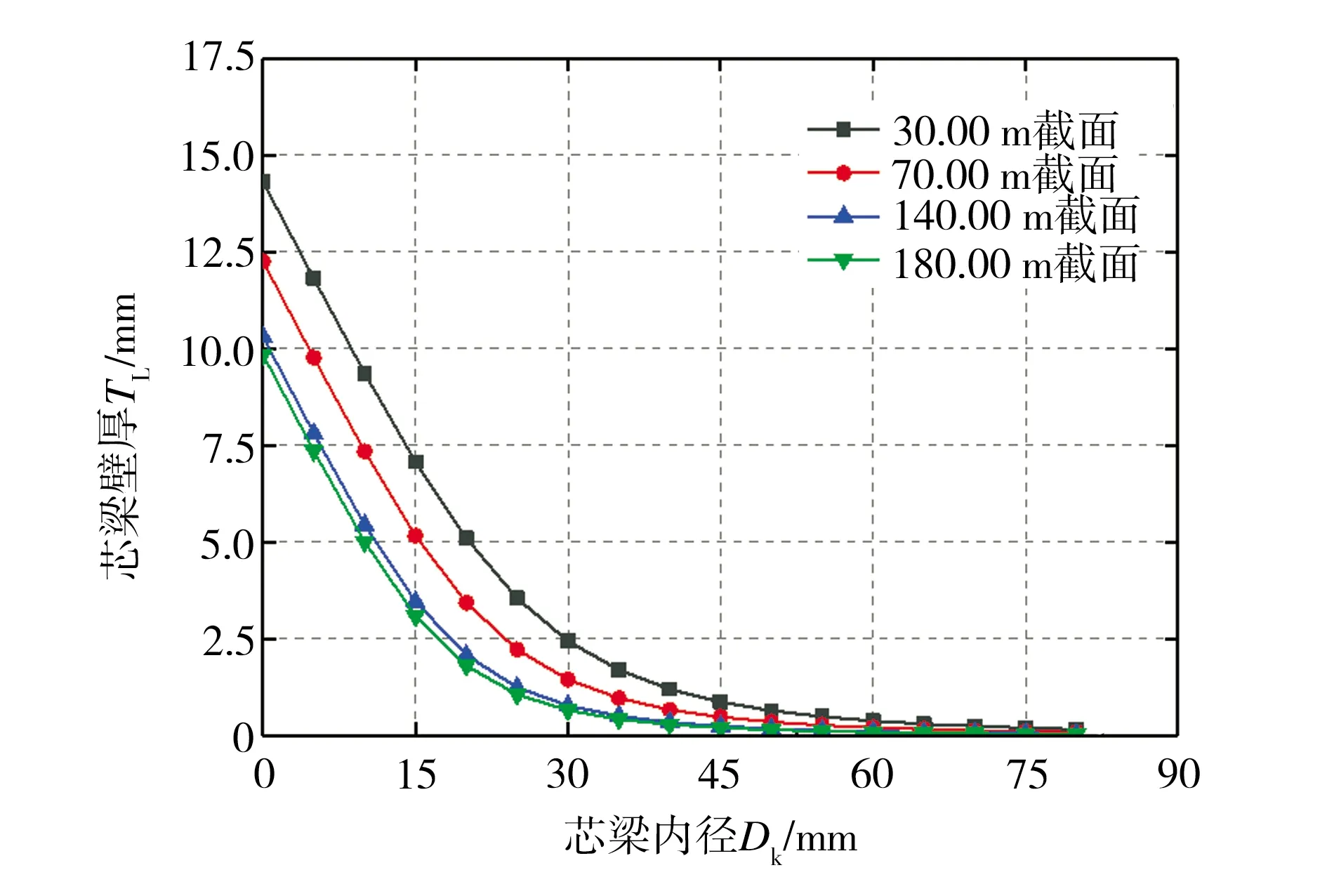
(a)芯梁壁厚TL

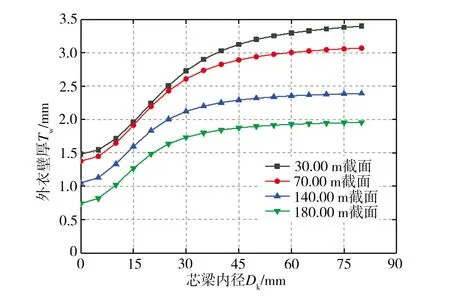
(b)外衣厚度Tw图5 TL和Tw随Dk的变化曲线Fig.5 Curves of TL and Tw variation with Dk

2.4.2 圆盘间距Dp的优化

圆盘间距Dp是固定每段外衣的两个圆盘之间的距离，增大圆盘间距Dp可以有效提高外衣的稳定性，但对芯梁刚度存在一定影响。为研究圆盘间距Dp对模型频率的影响程度，取芯梁内径Dk为12.70 mm，在ANSYS中分别建立Dp为10、30、50、70、90、110、130 mm等7种情况下太阳能塔塔身部分模型的有限元模型，并对模型结构进行静力分析，结果表明，改变Dp对模型弯曲刚度几乎无影响，当Dp从10 mm增至130 mm时，模型弯曲刚度仅增加10%。图6所示为太阳能塔塔身前3阶自振频率随Dp变化的曲线。从图6中可以看出，随着Dp的增加，塔身前3阶平动的频率均有提高，但增幅不大，在5.00%以内。这是因为Dp越大，每段外衣在其对应的芯梁中的振动参与程度也越大，使得芯梁刚度在有限范围内不断增大，从而导致结构频率小幅增加。为减小Dp带来的误差，应在满足外衣足够稳定的前提下，尽量减小Dp，故本研究中模型Dp设定为50.00 mm。

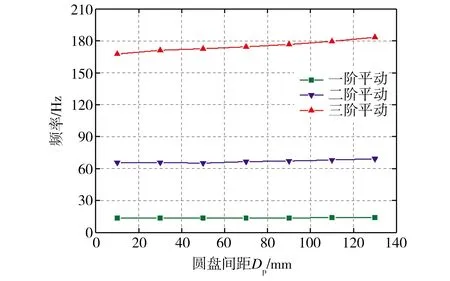
图6 不同圆盘间距下的结构频率Fig.6 Structure frequencies under different disc spacings

2.4.3 钢结构集热筒底盘厚度Td的优化

在设计集热筒模型底盘时，应充分考虑钢筋混凝土塔身与钢结构集热筒连接处存在的刚度突变，模型中钢筋混凝土塔身与钢结构集热筒部分采用螺丝连接，连接部分的刚度主要由集热筒底盘提供，对筒底厚度Td进行优化以精确模拟结构的前3阶频率及振型。在筒体结构整体质量不变的条件下，选取芯梁内径Dk为12.70 mm、圆盘间距Dp为50.00 mm，研究了筒底厚度Td分别为0.50、1.00、1.50、2.00、2.50 mm时模型自振频率及振型变化，结果分别如图7和图8所示。从图7中可以看出，改变Td可以调节模型的自振频率，尤其对第2、3阶的频率影响更为明显，这是因为增大底盘厚度可提高模型连接处的刚度。通过线性插值算法可得，当集热筒的Td为1.60 mm时，模型结构振动频率与设计目标频率最为接近。此外，结合图8所示结果可知，当Td小于1.50 mm时，筒底刚度过小，模型中集热筒不能与混凝土塔身形成有效的连接，全塔结构的振型在这一部位出现了严重的突变；当筒底厚度Td不小于1.50 mm时，全塔结构振型变化已不明显，表明集热筒与混凝土塔身形成了有效的连接，模型振动以前2阶频率为主，当Td为1.50 mm时，模型第1、2阶振型与原结构振型最为接近，位移最大相对误差小于15.00%，因此，针对本研究中的太阳能塔结构，取Td为1.50 mm可以达到最理想的模型设计效果。

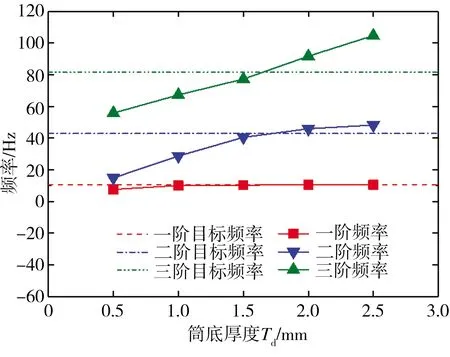
图7 不同底盘厚度下全塔模型频率Fig.7 Model frequencies of tower model under different chassis thicknesses

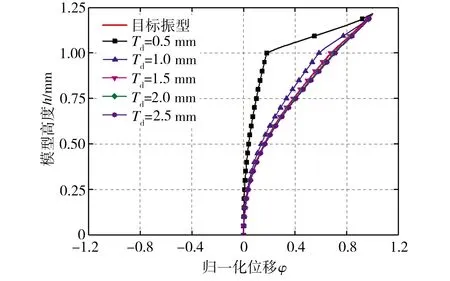
(a)第1阶振型

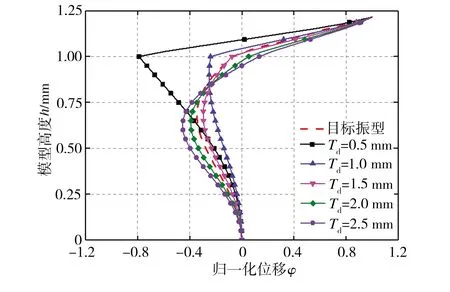
(b)第2阶振型

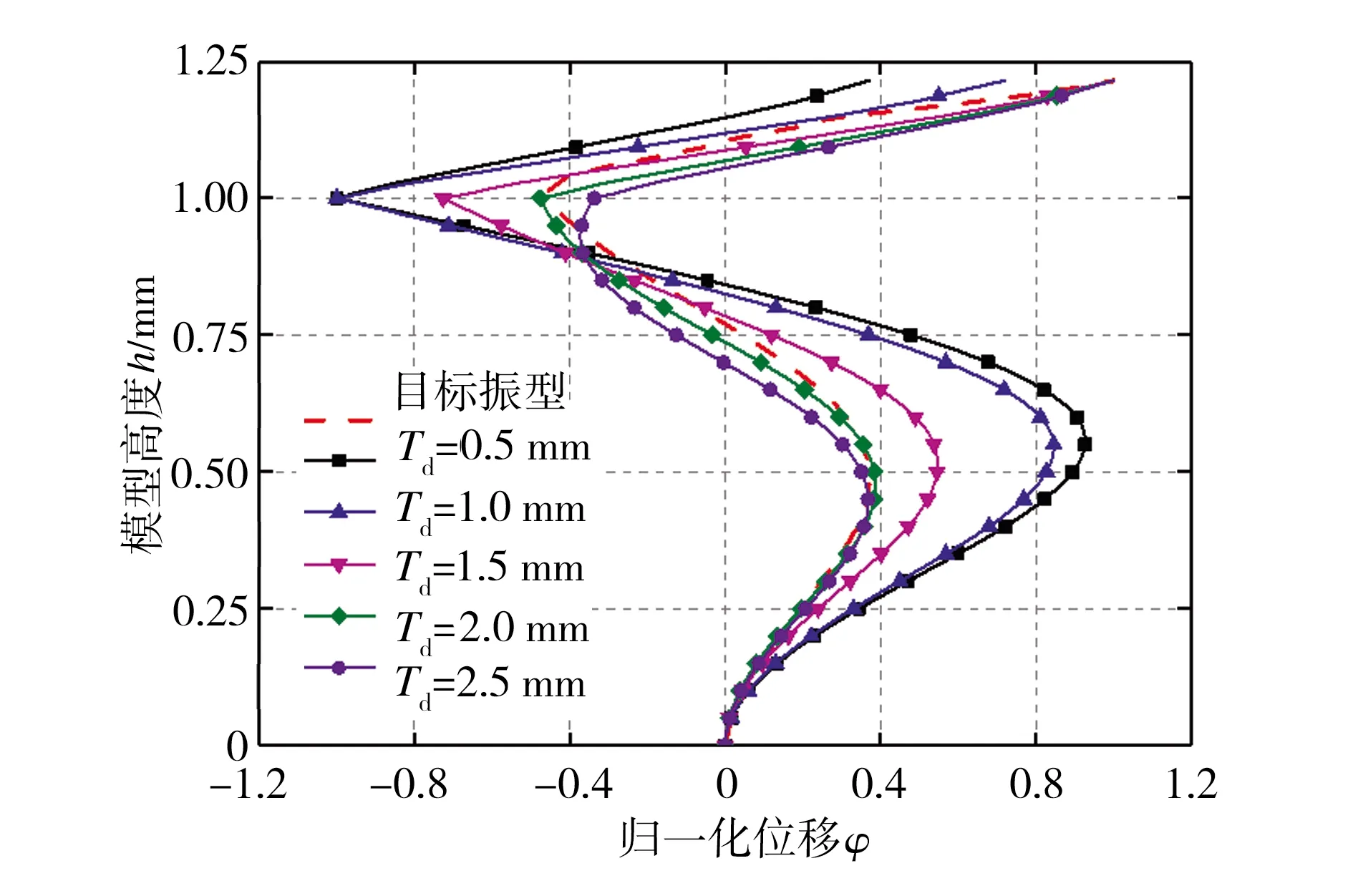
(c)第3阶振型图8 不同底盘厚度下的振型Fig.8 Mode shape under different chassis thicknesses

2.5 实际模型的制作及其动力特性

在综合考虑各项参数的影响后，选取Dk为12.70 mm、Dp为50.00 mm、Td为1.50 mm，设计制作的太阳能塔模型如图9所示。将模型与风洞底部用螺栓固结，并分别在模型顶部的横风向和顺风向安装加速度传感器，频率测试范围为1～18000 Hz，测试灵敏度约为5.11 PC/g，单个传感器质量为2.80 g，利用ANSYS对该模型进行模态分析及实际动力测试的结果如表3。由表3可知，ANSYS有限元模型前3阶频率与设计目标频率吻合度良好，最大误差为3.01%，模型横风向与顺风向实际动力测试结果完全相同，振动以第1阶弯曲振型为主，实测频率为9.80 Hz。此外，对模型的实际动力测试结果还表明，模型初始阻尼比小于0.30%，并且可在一定范围内实现阻尼比的精确调节，图10所示为模型阻尼比ξ为0.30%及调节至2.00%条件下，模型振动时顶部加速度的自由衰减曲线，其中g为重力加速度。

(a)芯梁骨架 (b)模型成品图9 实际模型Fig.9 Actual model

表3 模型频率对比Table 3 Model frequencies comparison

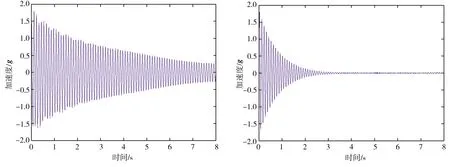
(a)ζ为0.30% (b)ζ为2.00%图10 模型振动自由衰减曲线Fig.10 Free attenuation curves of model vibration

3 结语

本文借助有限元软件设计了一种太阳能塔气弹模型，并对模型结构进行了优化分析，在此基础上实际制作了太阳能塔结构模型并进行了动力测试。分析及测试结果表明，圆环型芯梁可有效减小芯梁质量，增加外衣壁厚，降低模型加工难度；适当增加圆盘间距对模型频率影响较小，但可增加外衣的稳定性；调整集热筒底盘厚度对集热筒与塔身的连接刚度有明显影响；太阳能塔气弹模型较精确地模拟了原型结构前3阶频率及振型；模型初始阻尼比低于0.30%，较好地实现了对结构超低阻尼的模拟，可为此类低阻尼高耸结构多自由度气弹模型设计提供参考依据。