基于PSO优化的LCL型三相VSR改进无源控制策略

严运兵，高维士，马 强，王晓东，朱博文

(1.武汉科技大学汽车与交通工程学院，湖北 武汉，430065；2.湖北文理学院纯电动汽车动力系统设计与测试湖北省重点实验室，湖北 襄阳， 441053)

随着电力控制技术的发展，脉冲宽度调制(pulse width modulation， PWM)整流技术因其输出电压可控、入网谐波含量低、可双向变流等优点越来越受到重视，PWM整流器的控制策略[1]也受到研究人员的关注。传统L滤波器的三相电压源PWM整流器存在开关器件工作频率较高、电感值较大、相对谐波含量较高等缺点，而LCL滤波器不仅开关工作频率低、电感值小，同时对高次谐波具有更好的滤除效果，能够有效降低入网电流波形总谐波畸变率(total harmonic distortion，THD)，所以电压源整流器(voltage source rectifier，VSR)中的L滤波器逐步被LCL滤波器所代替。

LCL滤波器虽能降低入网电流波形总谐波畸变率，但由于滤波电容的引入增加了谐振现象，导致系统不稳定，因此一些新的控制策略应运而生，例如无阻尼控制策略[2]、滑模控制理论[3]、有源阻尼控制策略[4]、直接功率控制策略[5]等。文献[6]提出了一种基于自适应陷波滤波器的单环有源阻尼方法，同时利用网格阻抗估计算法，可以自适应地更新陷波滤波器参数以抵抗电网阻抗变化，借助于LCL滤波器的单回路有源阻尼策略，可以有效抑制谐振电流，实现稳定控制。高善成等[7]提出了基于欧拉—拉格朗日(Euler-Lagrange，EL)模型的三相LCL并网逆变器，将无源控制理论引入该系统的控制中，实现了对LCL滤波器谐振峰的抑制。郭利辉等[8]在基于同步旋转坐标系的LCL-VSR控制中,通过在电流环中增加陷波滤波器的方法实现了LCL滤波器的有源阻尼控制，有效抑制LCL滤波器的固有谐振。

无源控制(passivity-based control， PBC)是从系统的能量入手，设计的无源控制律可使系统能量按期望的能量函数分布，使得闭环系统满足无源性，以达到控制目的，其数学模型有EL模型和具有耗散的端口受控哈密顿(Port Controlled Hamiltonian with Dissipative，PCHD)模型。基于PCHD模型的互联和阻尼分配无源控制(interconnection and damping assignment PBC， IDA-PBC)算法的无源控制策略可以按系统的控制要求确定系统的能量分布，通过阻尼注入和互联矩阵，可有效降低谐振现象，提高整流系统的稳定性，同时系统结构简单，设计具有灵活性[9-10]。张林峰[11]提出了基于单相LCL型并网逆变器的无源控制策略，并加入了电容电压反馈，解决了传统LCL-VSR中无源控制阻尼提供不足问题，实现了控制系统零稳态误差跟踪。为改进统一电能质量调节器的控制性能，郑成才等[12]通过建立T型三电平逆变器的PCHD数学模型，采用IDA-PBC方法，设计了无源混合控制器，实现了对电能质量调节器的优化控制。文献[13]基于有源电力滤波器的PCHD数学模型，采用IDA-PBC方法，设计了自适应模糊控制器，实现了注入阻尼在线调整的无源混合控制。为此，本文以LCL滤波器的三相电压源脉冲宽度调制整流器为载体，通过建立具有耗散的端口受控哈密顿模型，构建基于互联和阻尼分配无源控制算法的改进的无源控制策略，利用粒子群算法对控制参数进行离线优化，并对控制系统进行仿真试验，验证其额定负载及负载突变等情况下基于IDA-PBC算法的无源控制策略的有效性，以期为实现LCL滤波器在较低开关频率下能有效降低入网电流波形总谐波畸变率及提高系统的稳定性提供参考。

1 LCL-VSR的PCHD模型

LCL-VSR主电路图如图1所示。ega、egb、egc是相电压幅值为Um的交流电网电动势，V；0为中性点，即三相电网的公共点；Lg为电网侧等效电感,H；uca、ucb、ucc为电容电压，V；L为整流器侧等效电感，H；Rg为电网侧等效电阻，为电感Lg、滤波电容Cf和电压源的等效电阻之和，Ω；R为整流器侧等效电阻，为电感L和开关器件的等效电阻之和，Ω；vk为整流器输入端电压(k=a，b，c)，V；ik为整流器输入端电流，A；ig，k为电网侧输入电流，A；udc为输出电压，V；电阻RL为等效负载，Ω；C为直流电容，F。

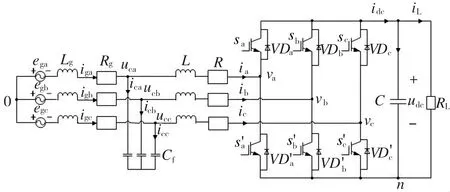
图1 LCL-VSR主电路图Fig.1 The main circuit diagram of LCL-VSR

为建立模型需要，现做以下假设：①电源为对称电源，滤波电感物理特性相同；②开关管为理想状态；③设sa、sb、sc为整流器单极性二值逻辑开关函数。根据基尔霍夫电压、电流定律，由图1可得三相VSR在三相abc坐标系下的数学模型为

(1)

采用等功率变换后可获得两相旋转dq坐标系下的数学模型为

(2)

式中，ω为交流电网电动势的空间矢量旋转角频率。

设x1=Lgigd、x2=Lgigq、x3=Lid、x4=Liq、x5=Cfucd、x6=Cfucq、x7=Cudc，则系统总能量存储函数为

(3)

根据假设及式(2)可得

(4)

由公式(3)可将式(4)转换为PCHD方程的形式为

(5)

根据文献[14]，由能量存储函数(H(x))公式验证可得，用PCHD模型描述的LCL-VSR具有严格无源性设计。

2 VSR无源控制策略

2.1 IDA-PBC无源控制器设计思想

对基于PCHD方程的控制策略有基于无源性的互联控制、标准反馈互联控制和基于循环无源性的互联控制等，考虑到实际需要及控制器设计实现的难易程度，可以采用互联和阻尼分配无源控制(IDA-PBC)方法进行设计，不仅可以处理系统的稳定性,同时也使动态性能有一定提高，从而获得最佳的控制效果。

IDA-PBC的控制思想是确定一个控制律u,使系统闭环的PCHD模型为

(6)

式中：Jd(x) 为新的互联矩阵，Jd(x) =J(x)+Ja(x)，Ja(x)为注入的互联矩阵；Rd(x) 为新的耗散矩阵，Rd(x)=R*(x)+Ra(x)，Ra(x)为阻尼注入矩阵；Hd(x) 为总能量存储函数，Hd(x)=H(x)+Ha(x)，Ha(x)为注入的能量函数，同时满足xref=argmin(x)，xref为期望的平衡点。

2.2 无源控制器设计

2.2.1 期望稳定平衡点确定

当VSR系统在期望的单位功率因数下运行时，各期望目标值可按下式给定

(7)

式中，Um为相电压幅值，V；Im为稳定运行时交流相电流幅值，A。

根据假设及公式(7)，则有期望的平衡点(xref)为

(8)

其中Im可由功率守恒得

(9)

2.2.2 无源控制器设计

根据公式(5)和公式(6)，并利用IDA-PBC方法进行无源控制器设计，可得

(10)

由于阻尼注入，直接影响系统响应快慢，则可通过注入适当阻尼方式，实现能量存储函数快速收敛到期望的平衡点。取Jd(x)=J(x)，Rd(x)=R*(x)+Ra(x)，其中Ra(x)=diag(ra1ra2ra3ra4ra5ra61/ra7)，则式(10)可变为

(11)

令

(12)

对式(12)取矢量函数，则可得无源控制方程

(13)

对于平衡电网输入，式(11)中u为定值，可将开关函数sd、sq作为整流器控制量。根据式(13)，利用IDA-PBC方法可确定系统在期望平衡点xref处最小能量的sd、sq值分别为

(14)

设K(x)为x7的函数，由可积性及IDA-PBC控制理论[14]的条件可得

(15)

式中，A1、A2、A3、A4、A5、A6为待定常数。

由式(13)及式(15)可得

k7=

(16)

利用系统在xref处功率守恒原理，可得

(17)

由k1、k2、k3、k4、k5、k6、k7确定Ha(x)为

(18)

而

Hd(x)=H(x)+Ha(x)

(19)

则有

>0

(20)

从而能量函数Hd(x)的海森矩阵式(20)是正定的，满足最小值条件。

将k3、k4、k5、k6代入式(14)，可得基于IDA-PBC算法的无源控制器的开关函数为

(21)

2.2.3 控制器的改进设计

为提高控制器的控制效果，本文采用包含全部控制变量的比例偏差形式的IDA-PBC控制算法。

假设k1=k1(x1)，k2=k2(x2)，k3=k3(x3)，k4=k4(x4)，k5=k5(x5)，k6=k6(x6)，k7=k7(x7)。依据可积性和IDA-PBC控制理论的条件，则有

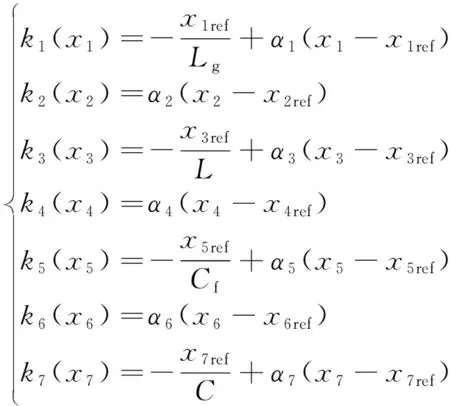
(22)

式中，α1、α2、α3、α4、α5、α6、α7为比例优化参数，其值均大于零。

将式(22)代入式(14)，可得基于IDA-PBC算法的无源控制器改进后的开关函数为

(23)

由式(9)和式(23)可得基于IDA-PBC算法的LCL-VSR无源控制系统框图,如图2所示。

2.3 基于粒子群算法离线控制参数优化

离线优化过程有多种方法，其中粒子群算法(Particle Swarm Optimization，PSO)因其结构简单、易于使用、高收敛率及满足最小存储要求，特别是PSO更少依赖于初始点的集合，促使其收敛算法稳健性好，已得到了学术界的高度重视[15-17]，因此本文采用粒子群算法获得控制参数。

2.3.1 基本粒子群算法

输出性能指标函数[18]为：

(24)

在一个D维空间有n个粒子的种群中寻找最优值时，粒子根据如下公式来更新自己的速度和新的位置：

(25)

(26)

2.3.2 离线参数优化

上述PSO寻优的初始化粒子(p)，是包含α3、α4、α5、α6的一组四维向量，其输出性能指标为适应度值。以额定负载为基础通过以上更新，当适应度值满足所设定的性能指标时，即终止寻优，得到群体极值gbest，其中σ取0.6，c1、c2均取2，最大迭代次数为1200，粒子群规模取50，最小适应度值为0.001。

3 仿真分析

3.1 仿真设计

利用Matlab-Simulink软件，根据式(9)和式(23)搭建基于IDA-PBC算法的无源控制系统仿真模型。仿真试验的主要参数如表1所示，额定负载电阻RL=50 Ω，过载时电阻RL=25 Ω，轻载时电阻RL=100 Ω。

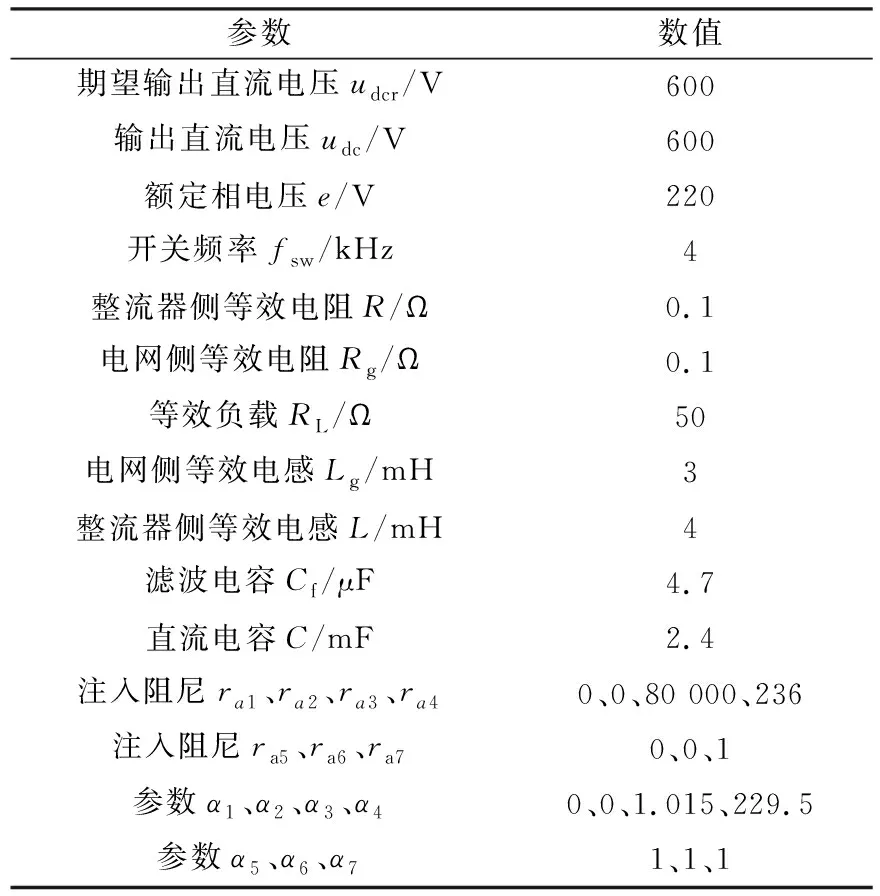
表1 仿真试验的主要参数Table 1 Main parameters of the simulation experiment

3.2 仿真结果及分析

3.2.1 额定负载时的谐波分析

额定负载时控制系统的a相网侧电流谐波频谱如图3所示，其中作为对比的电压前馈解耦控制L-VSR，除不含有滤波电容Cf、其总电感与LCL-VSR总电感相等外，其它参数未变。从图3中可以看出，改进的基于PSO优化LCL滤波器较电压前馈解耦控制L滤波器各次谐波的幅值及入网电流波形总谐波畸变率(THD)均有明显降低， 其中THD值由5.94%下降至2.27%，并无谐振频率出现，特别是在1.77 kHz(35次谐波)处无谐振点，这是因为，改进后的基于PSO优化LCL滤波器对开关频率处的高次谐波(80次)能够产生较好的滤除效果[19]，同时对10～40次谐波段谐波具有抑制作用[20]，由此表明，基于PSO优化改进的IDA-PBC算法的LCL-VSR无源控制策略对谐振频率有良好的抑制作用。从图3中还可看出，改进的基于PSO优化LCL滤波器较未改进的基于PSO优化LCL滤波器的谐波明显减少，入网电流波形总谐波畸变率(THD)也有所降低，这是因为，改进后的基于PSO优化LCL滤波器采用比例偏差形式IDA-PBC控制算法，由公式(22)可知，算法中包含了αi(xi-xiref)，意味着IDA-PBC控制算法引入了igd、igq、id、iq、ucd、ucq、udc等比例偏差反馈，而比例偏差反馈的引入会增加系统动态反馈性能，使控制系统的性能得到明显改善，同时THD的值随着α3增大而降低，但输出电压会有超调，而增加α4会使THD降低，输出电压超调量不变，因此，通过相互调整αi，不仅使谐波含量有所降低，而且有效消除了谐振现象，同时系统的稳定性也有所改善。

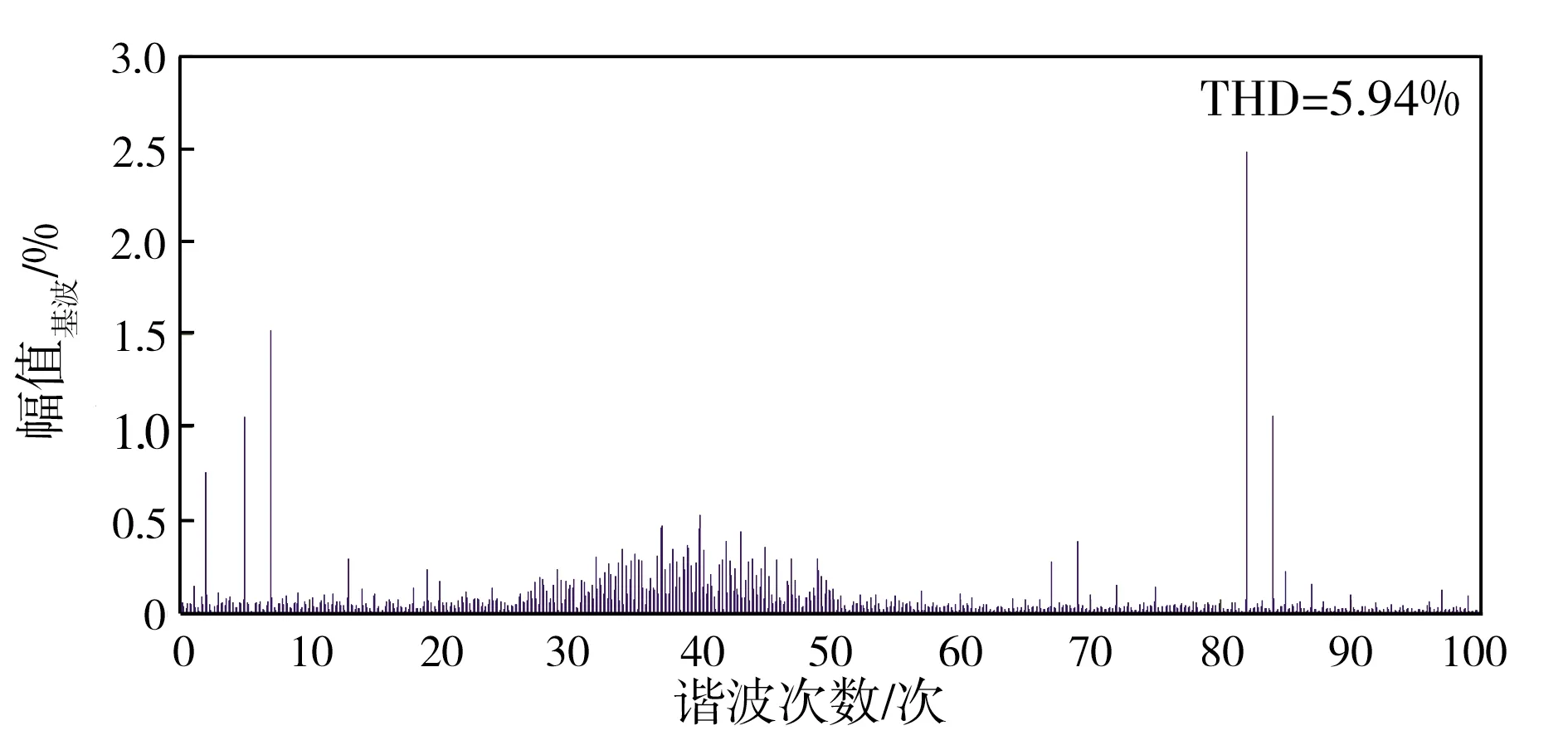
(a)L滤波

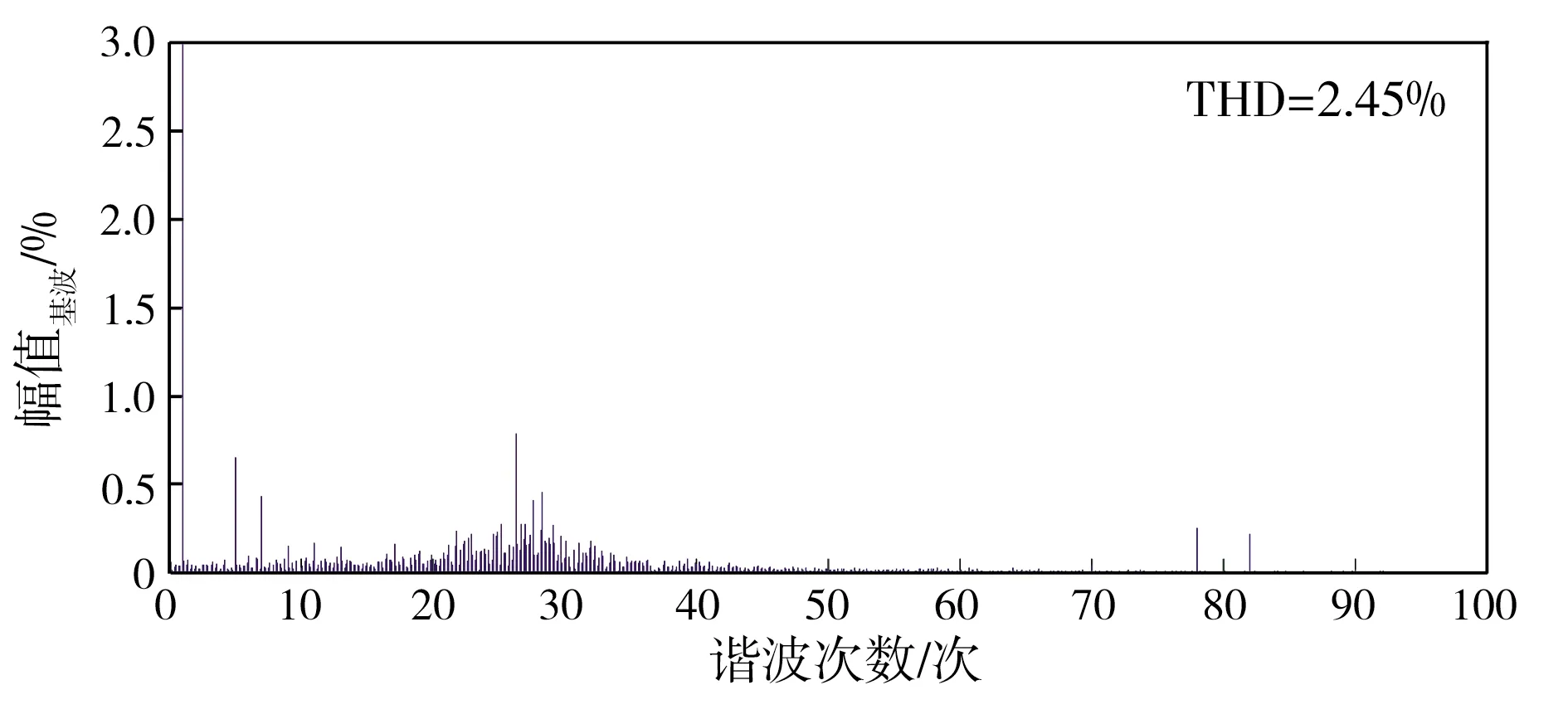
(b)未改进的基于PSO优化LCL滤波

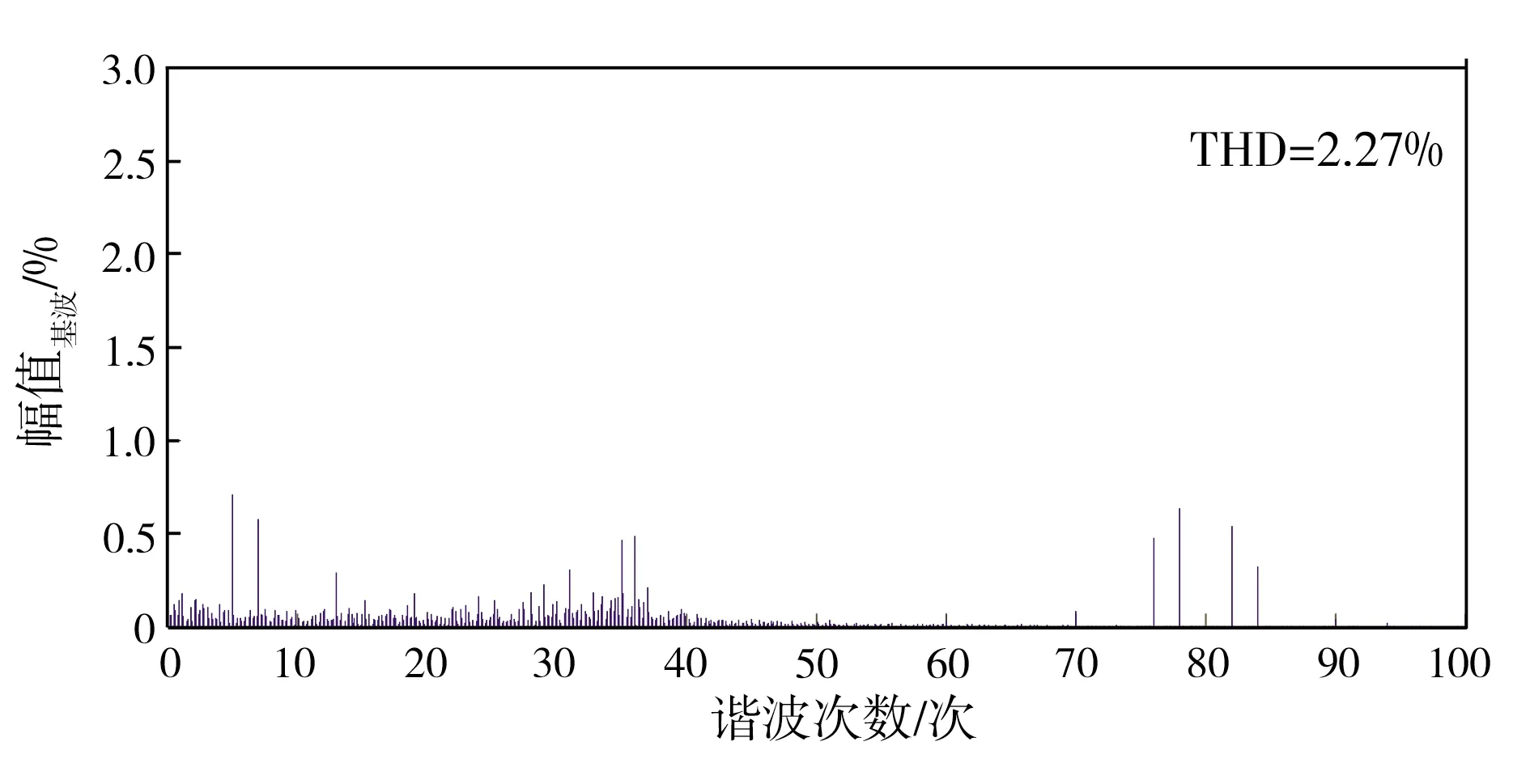
(c)改进的基于PSO优化LCL滤波图3 额定负载时控制系统的a相网侧电流谐波频谱Fig.3 Harmonic spectrum of a-phase grid side current of control system at rated load

3.2.2 稳态性能分析

额定负载(RL=50 Ω)、过载(RL=25 Ω)、轻载(RL=100 Ω)情况下控制系统的仿真结果分别如图4、图5、图6所示，其中，u1为未改进的基于PSO优化的IDA-PBC算法LCL-VSR直流侧输出电压，u2为基于PSO优化的改进IDA-PBC算法的LCL-VSR直流侧输出电压，u3为未经PSO优化的改进IDA-PBC算法的LCL-VSR直流侧输出电压；i1为未改进的基于PSO优化的IDA-PBC算法LCL-VSR直流侧输出电流，i2为基于PSO优化的改进IDA-PBC算法的LCL-VSR直流侧输出电流，i3为未经PSO优化的改进IDA-PBC算法的LCL-VSR直流侧输出电流。

从图4中可以看出，在额定负载时，u1与u2、i1与i2进入稳定状态的时间几乎相同，而u3、i3进入稳定状态的时间稍长，这表明经PSO优化后系统的控制效果得到了提高；从图5和图6中可以看出，在过载、轻载条件下，u1与u3、i1与i3仿真曲线基本重合，而u2、i2进入稳定状态的时间开始提前，其中在轻载情况下，u1进入稳定状态的时间为55.5 ms，u2进入稳定状态的时间缩短至16.5 ms，i1进入稳定状态的时间为50.5 ms，i2进入稳定状态的时间缩短至15.8ms，同时u1超调量在1 V左右，由此表明，改进并经PSO优化的控制策略效果最佳。

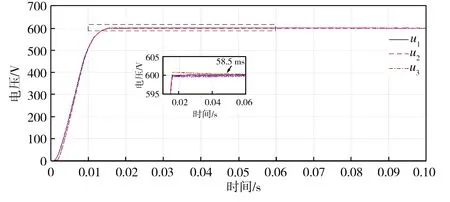
(a)直流侧电压对比

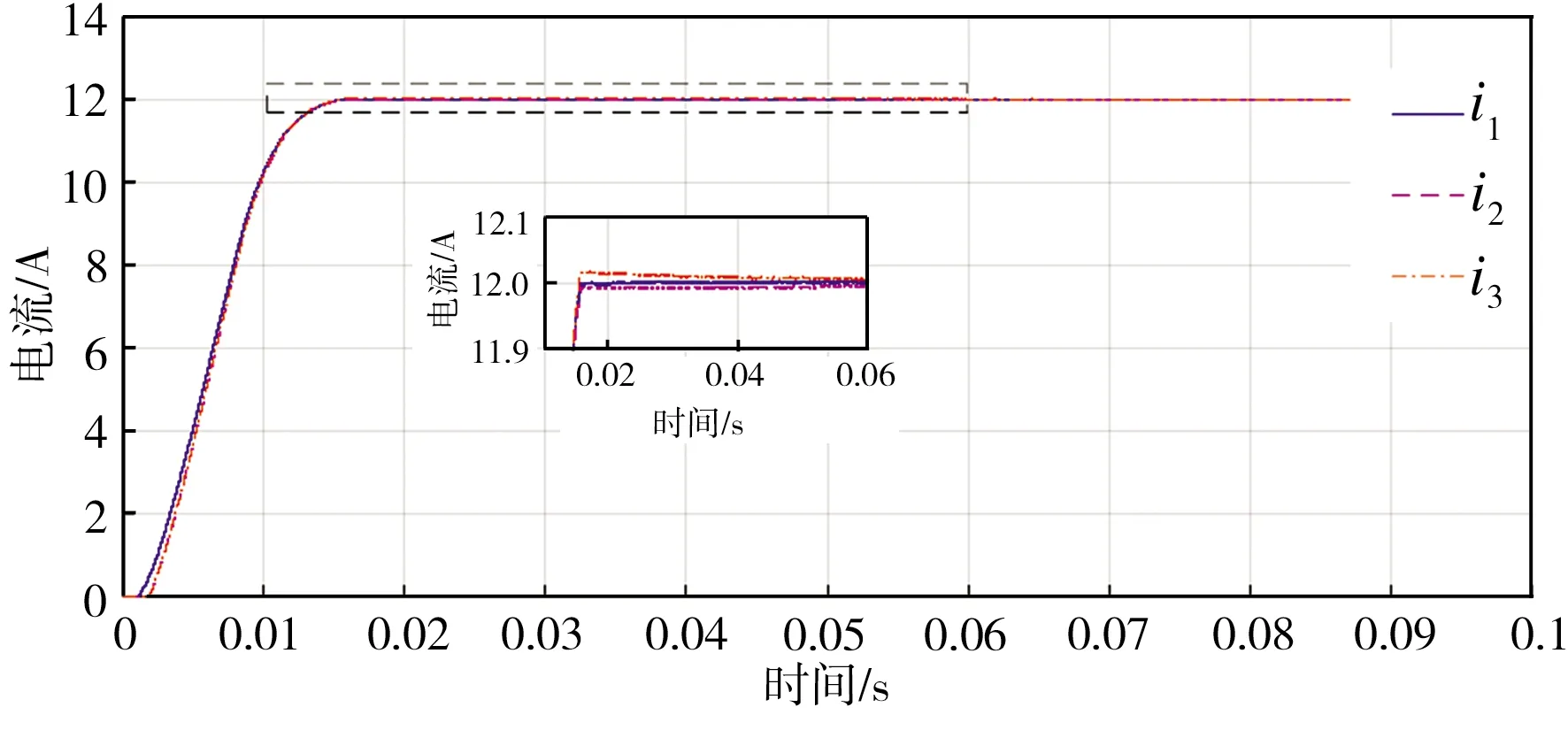
(b)直流侧电流对比图4 RL=50 Ω时控制系统的仿真结果Fig.4 Simulation results of the control system at RL=50Ω

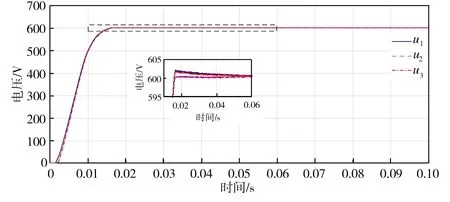
(a)直流侧电压对比

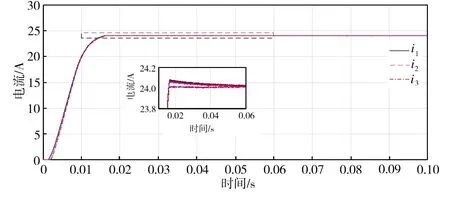
(b)直流侧电流对比图5 RL=25 Ω时控制系统的仿真结果Fig.5 Simulation results of the control system at RL=25Ω

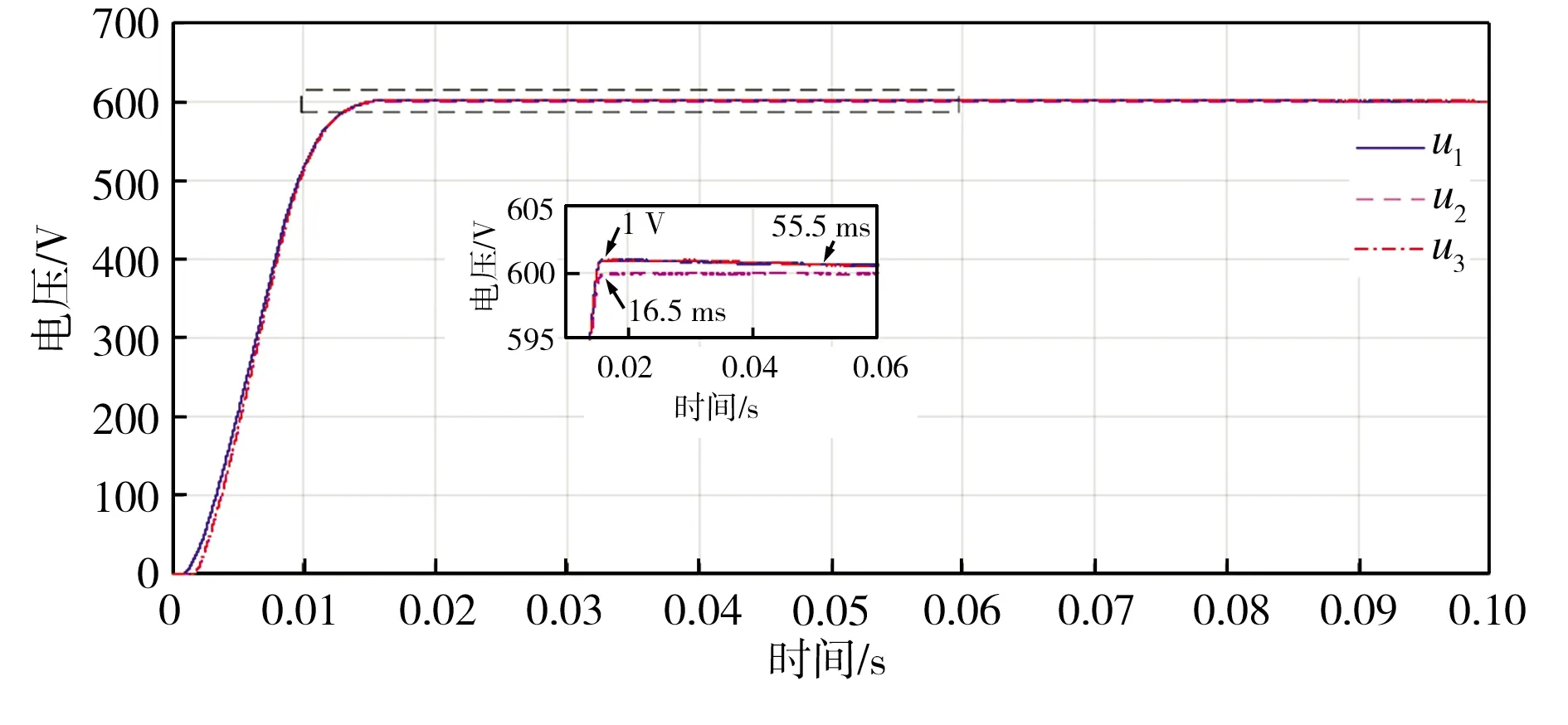
(a)直流侧电压对比

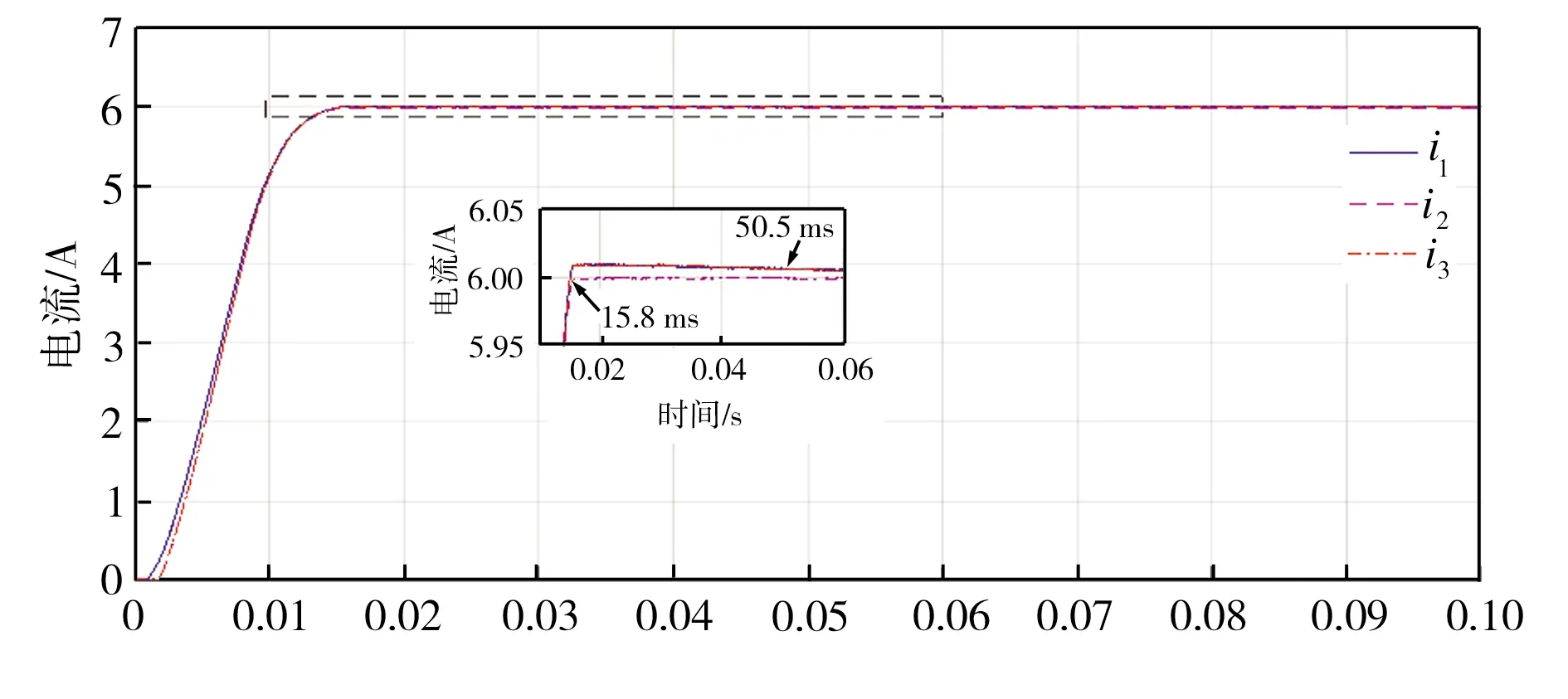
(b)直流侧电流对比图6 RL=100 Ω时控制系统的仿真结果Fig.6 Simulation results of the control system at RL=100Ω

3.2.3 负载突变情况下的暂态性能分析

暂态负载突变情况下控制系统的仿真结果如图7所示。为了检测基于PSO优化的改进IDA-PBC算法的LCL-VSR无源控制系统抗扰动能力及暂态性能，分别在图7中a点(0.1 s)、b点(0.2 s)、c点(0.3 s)和d点(0.4 s)处进行负载突变测试，各突变点处电阻的初始值至终止值的范围分别为50～100 Ω、100～50 Ω、50～25 Ω和25～50 Ω。通过对图7进行分析得到突变点处电流、电压误差值及突变前后其进入稳态的时间差如表2所示，其中，Δudc为突变点处udc与稳定值间的最大误差值，Δt1为突变前后udc进入稳态的时差，ΔiL为突变点处iL与稳定值间的最大误差值，Δt2为突变前后iL进入稳态的时差。从表2中可以看出，基于PSO优化的改进IDA-PBC算法的LCL-VSR无源控制系统，在负载突变时电流、电压的波动量都较小，电压与电流的波动量分别在1.50%、0.71%(波动量的最大值/期望值)以内，且进入稳态的时差在150 ms以内，由此表明，该控制策略对负载突变的抗扰动能力及暂态性能较好。

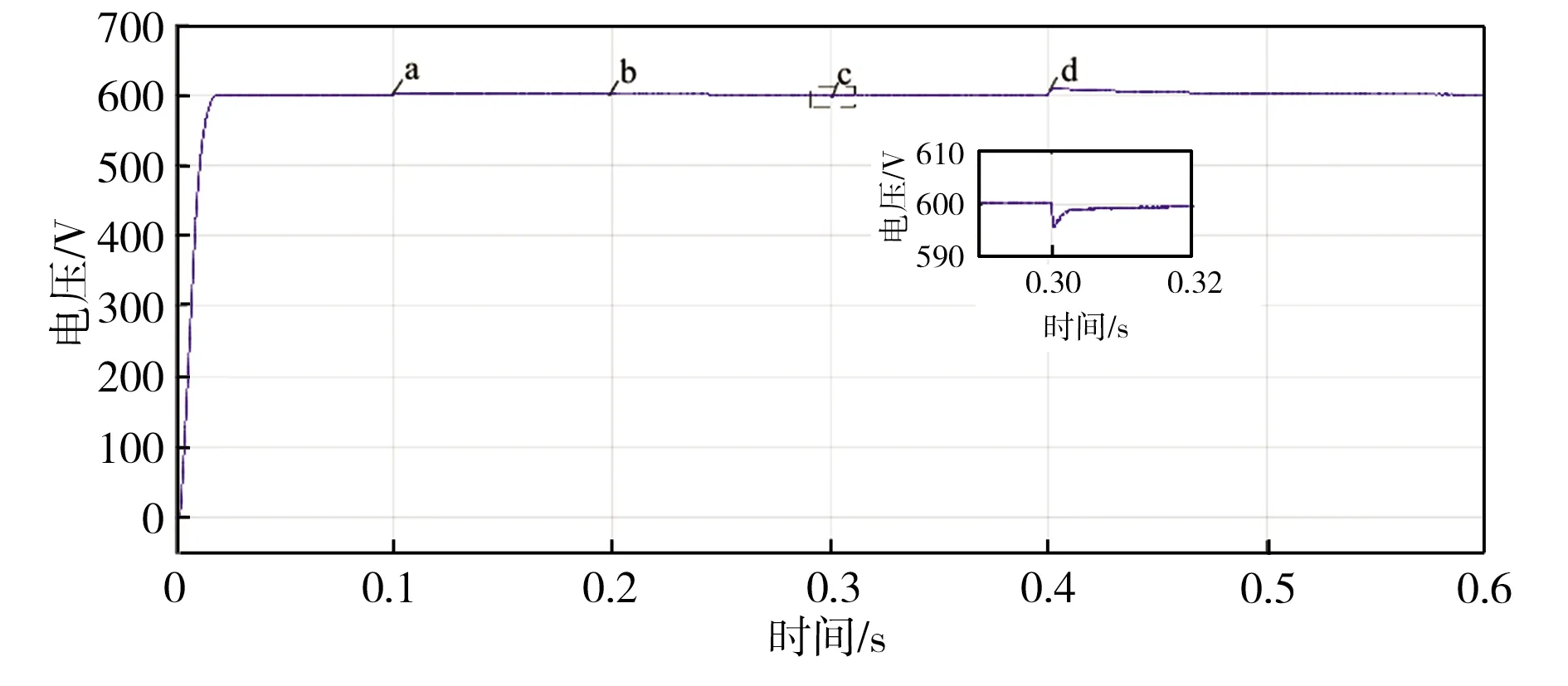
(a)含参数LCL-VSR的直流侧电压udc突变波形

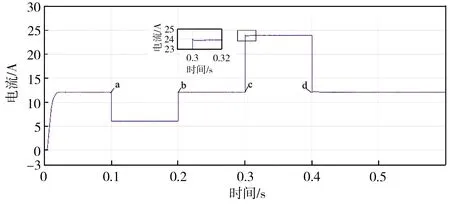
(b)含参数LCL-VSR的直流侧电流iL突变波形

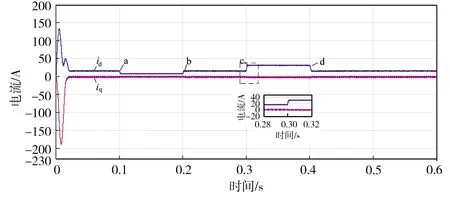
(c)含参数LCL-VSR的网侧电流dq分量突变波形图7 暂态负载突变情况下控制系统的仿真结果Fig.7 Simulation results of the control system under abrupt change of transient load

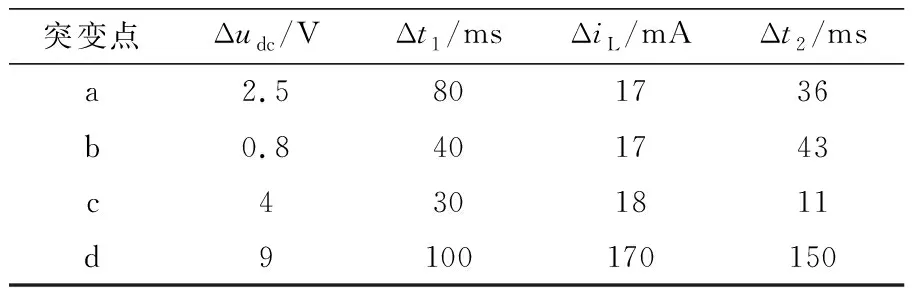
表2 突变点处电流、电压误差值及突变前后进入稳态的时差Table 2 Error values of current and voltage at the sudden change point and the time difference before and after the sudden change

3.2.4 功率因数分析

暂态负载突变情况下系统的功率因数和网侧电压、电流相位关系如图8所示。对于PWM整流控制系统，网侧电压与电流的相位关系直接影响其控制效果，对基于PSO优化的改进IDA-PBC算法的LCL-VSR无源控制系统是否能始终保持单位功率因数以及网侧电压与电流同相位稳定运行，将直接决定控制策略的好坏。从图8 (a)中可以看出，在a、b、c、d四点发生负载突变的整个过程中，系统始终保持单位功率因数运行；从图8 (b)中可以看出，网侧电压与电流在0.1 s和0.2 s突变前后都保持同相位稳定运行，由此表明，基于PSO优化的改进IDA-PBC算法的LCL-VSR在负载突变时能够实现高功率稳定运行。

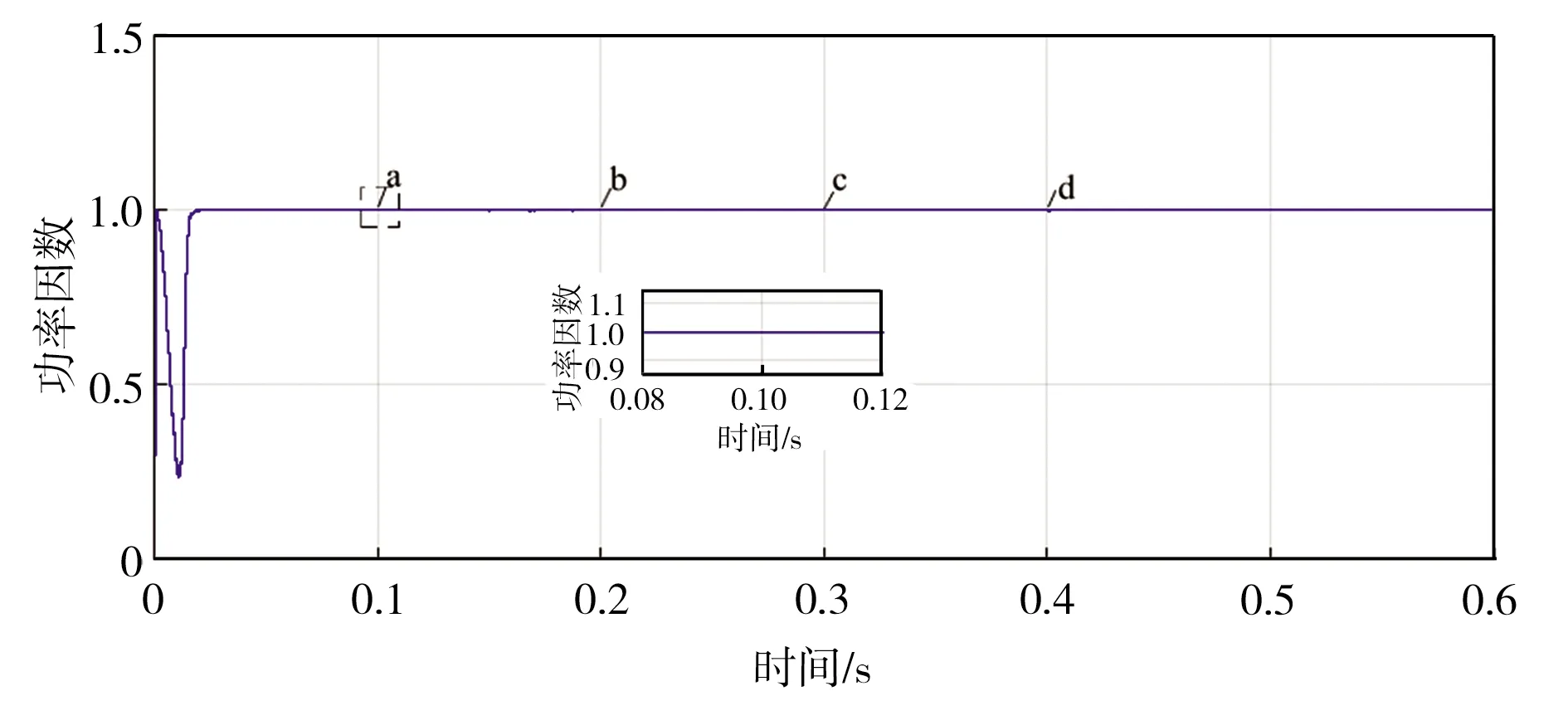
(a)含参数LCL-VSR在负载突变过程中的功率因数

4 结论

(1)基于PSO优化的LCL型三相VSR改进的无源控制策略能有效降低网侧电流的谐波含量和抑制谐振现象，使脉冲宽度调制整流器的整体性能得到有效提升。

(2)优化后的控制系统抗扰动能力及暂态性能都有明显提高，具有较好的稳定性和鲁棒性。