动车所调车作业计划优化模型与算法

殷 迪，唐秋华，张子凯，韩大勇

(1. 武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉,430081)

为保证行车安全，动车组必须在夜间返回动车所进行维修，维修方式通常为一级修，主要包括检修和清洗两项作业，分别在检修股道和清洗股道上完成，此外，动车所还配备有一定数量的存车股道，主要用于动车组待检时的临时停放及检后预留停放。动车所需根据动车组的运用计划编制调车作业计划，即在动车组出入动车所时间确定的前提下，合理分配每辆动车组的检修、清洗和停放股道及占用相应股道的时间，在确保动车组按计划运行的同时顺利完成一级修任务，为其下一个行程提供安全保障。传统的调车作业计划编制主要依赖于调度人员的经验，存在编制难度大、效率低等不足，加之我国动车组数量不断增多、股道资源持续扩增，如何科学、有效且快速地完成调车作业计划编制，是当前亟需解决的问题。

根据优化目标的不同，调车作业计划编制问题主要分为两类：①单目标优化问题，如最小化动车所内总延误时间[1]，最小化调车总钩数[2]，最小化动车组检修完成时间[3]，最大化股道利用率[4]等。②多目标优化问题，如最小化检修区无效占用时间和调车路径费用[5]，最大化存车线利用率和减少调车作业走行距离等[6]，最小化总延误时间、检修区无效占用时间、拥堵时间和维修成本[7]。基于构建的优化模型，求解调车作业计划编制优化问题的方法主要有精确算法和启发式算法，不过前者虽然可求得问题的最优解，但求解效率偏低，而后者则能在较短时间内求得问题的近优解，实用价值较高，因此，本文将动车所调车作业计划编制问题转化为带有不定加工时长的Job-Shop调度问题，以动车组在存车线上的总预留时间最大化为目标函数，建立动车所调车作业计划编制优化模型，设计了求解该模型的启发式算法，并借助实验算例验证了模型和算法的有效性。

1 问题描述

图1所示为典型的动车组一级维修流程示意图。当动车组进所后，先后通过存车区1、作业区、存车区2，最后出所。存车区1可用于停放刚入所的动车组，当作业区有可用的作业股道时，也可不在存车区1停留直接进入作业区作业；清洗和检修作业在作业区内完成，每项作业时长须满足标准作业时间，且两项作业之间的顺序是不固定的；存车区2停放完成全部维修工作且等待出所的动车组。动车组在动车所内的调车路径包含动车组从存车区1到作业区的转线、作业区内部的转线和作业区到存车区2的转线，转线时间均按标准作业时间进行。动车组转线时必须满足股道时空相容性，如果下一作业区域的股道已全被占用，动车组必须停在当前股道进行等待。因此，可将动车所调车作业计划编制问题描述为加工时长不定、加工顺序不定的Job-Shop调度问题。在实际作业现场，动车所作业区配备的检修设备往往能力有限，是动车所检修能力的瓶颈，对动车组检修效率影响较大[5]，故而应尽量减少动车组对作业区股道的不必要占用，以便提高检修设备利用率和动车所检修吞吐量，当动车组检修作业完成后，应尽快将动车组调入存车区2等待出所，确保每辆动车组按规定时刻出所，避免延误。

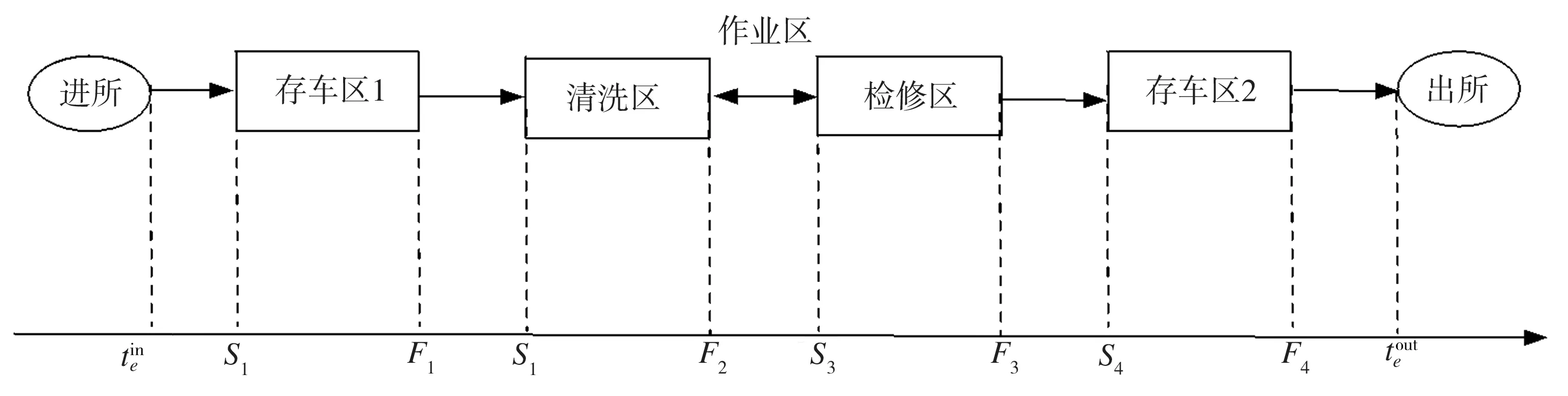
图1 动车组一级维修流程Fig.1 First-level maintenance procedure of EMU

2 MIP优化模型构建

2.1 符号说明

集合：

E动车组集合，索引为e,e∈{1,2,...,Ne}。

Z作业区集合，索引为z,z∈{1,2,3,4}，分别代表存车区1、清洗区、检修区和存车区2。

Dz作业区作业线集合,索引为Dz,d,d∈{D1,D2,D3,D4}。

R相邻作业线区转线股道集合，索引为r，r′表示股道d和d′之间的转线股道，若存在连通关系，则rd,d′=1 ；否则为0。

参数：

τr标准转线时间,min。

pz各作业区标准作业时间,min。

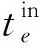
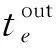
n每条股道上执行的第n个作业，n={1,...,Nd}。

l每个动车组执行的第l个作业，l={1,2,3,4}。

中间变量：

Sez连续变量，动车组e占用作业区z的开始时刻。

Fez连续变量，动车组e占用作业区z的结束时刻。

Bdn连续变量，股道d的第n个作业的开始时刻。

Tdn连续变量，股道d的第n个作业的结束时刻。

决策变量：

Xezl0-1变量，动车组e的第l个操作在作业区z执行。

Yezdn0-1变量，动车组e在作业区z的股道d上执行的第n个操作。

2.2 目标函数

当动车组检修作业完成后，应尽快将其调入存车区2准备出所，动车组在存车区2上总预留时间越长，准备就越充分，对作业区股道的不必要占用时间就越短，以动车组在存车线上的总预留时间最大化为目标函数，表达式为

(1)

2.3 约束条件

分配约束：每辆动车组必须进行清洗和检修作业，每项作业仅需执行一次，且两项作业之间无固定先后顺序，孰前孰后均可，则有

(2)

(3)

每辆动车组需要遍历存车区1、清洗区、检修区和存车区2共四个区域，且在每个区域内，每辆动车组只能占用一条股道，则有

(4)

给定股道d的第n个作业最多可进行一个作业，则有

(5)

在任意给定的股道d上，前面的作业先分配后才能分配后面的作业，则有

∀d∈Dz,∀n∈Nd

(6)

定时约束：如果动车组e在作业区z的作业确定为股道d上的第n个作业，则该作业的起止时刻等于动车组e在作业区z上的起止时刻，其中M是一个足够大的数，有

Sdn≤Bez+M(1-Yezdn),

∀e∈E,∀z∈Z,∀d∈Dz,∀n∈Nd

(7)

Sdn≥Bez-M(1-Yezdn),

∀e∈E,∀z∈Z,∀d∈Dz,∀n∈Nd

(8)

Fdn≤Tez+M(1-Yezdn),

∀e∈E,∀z∈Z,∀d∈Dz,∀n∈Nd

(9)

Fdn≥Tez-M(1-Yezdn),

∀e∈E,∀z∈Z,∀d∈Dz,∀n∈Nd

(10)

如果动车组e′在动车组e后进入作业区z的股道d，动车组e′在该作业区的开始时间不小于动车组e在该作业区的结束时间，则有

Be′z′≥Tez-M(2-Yezdn-Ye′z′d,n+1),

∀e,e′∈E,∀z,z′∈Z

(11)

动车组e在工作区z的停留时间不小于该区域标准作业时间，则有

(12)

转线约束：转线作业时长约束，即动车组e在前一区域z的结束时刻加上通过转线股道r的作业时间等于下一区域z′的开始时刻，则有

(13)

(14)

上述MIP模型是一个具有空间、时间二维特性、约束条件复杂的组合优化问题，随着动车组数目、动车所股道数目的增加，将会产生“组合爆炸”，而在实际的调车作业现场，调度员期望能快速生成近优解乃至最优解，考虑到现场操作需要的易用性和可解析性，拟设计规则组合算法对问题进行求解。

3 调车作业计划编制算法

为了科学、有效、快速地编制动车所调车作业计划，本文设计的求解算法融合了“先到先加工”“股道均衡分配”“股道无效占用时间最小化”等3种分配规则，并设计“冲突消解策略”以保证调车作业计划的可行性。

3.1 先到先加工规则

动车所确定动车组的运用计划后，动车组入所的时刻随之确定。根据先到先加工的原则，获得动车组入所后作业分配的先后顺序。

3.2 股道均衡分配规则

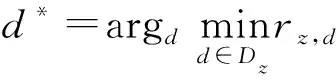
3.3 股道无效占用时间最小化规则

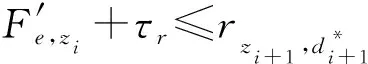
(15)

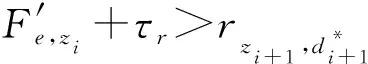
(16)

3.4 冲突消解策略

3.5 调车作业计划编制步骤

当动车所给定动车组运用计划后，基于上述的作业分配规则及策略，动车组的调车作业计划编制具体步骤如下：

步骤1：初始化动车所一级检修的基本参数Dz、pz等，设定每条股道的使用时间窗Time_Window(d,n)及其最早可用时间节点rz,d为0，根据“先到先加工规则”确定动车组的分配顺序π(e)。

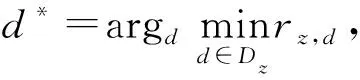
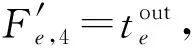
步骤5：令e=e+1，返回步骤 1，直至所有的动车组分配完，调车作业计划编制完成。

4 算例实验与分析

为了验证上述模型和算法的有效性，本文设计了启发式算法(HEU)与精确算法求解的对比实验。实验计算机配置：CPU 为Intel core i5 2.3 GHz，内存为8.00 GB 2133 MHz，启发式算法求解软件为Matlab，精确算法求解器(MIP-Solver)为GAMS24.0/Cplex。借助实验首先验证模型和算法的有效性，再将所提出的启发式算法与调度问题中常见的启发式算法进行比较，并评估解的质量，最后讨论目标值和运算时间随股道资源状态变化的变化趋势。

4.1 MIP-CPLEX对比实验

表1所示为动车组运用计划案例。案例一、二中的动车组EMU 1-8进出所时刻均为动车所的实际运用计划，其一级检修参数在表1中给出，标准转线时间都为τr=5 min。假设股道资源可变，分别设置不同区域的股道条数，以股道状态I为例，4-2-3-6表示存车区1的存车线条数为4条，清洗线2条，检修线3条，存车区2的存车线条数为6条。同理，设置股道资源状态II：4-2-3-7，III：4-2-3-8，IV：4-2-4-6，V：4-2-4-7，VI：4-2-4-8, VII: 4-2-5-6，VIII：4-2-5-8。在下述实验中，分别改变动车组的数量、股道资源的状态来获得不同的实验算例。

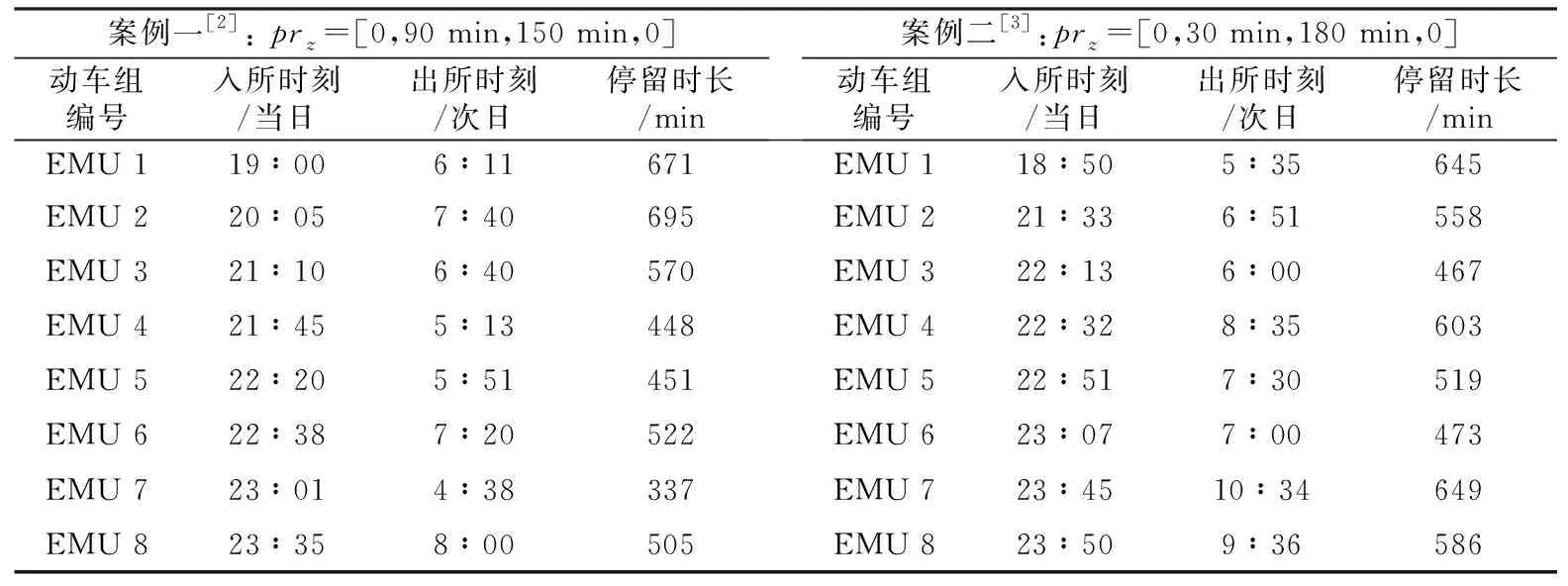
表1 动车组运用计划案例Table 1 EMU rolling stock cases

为了验证上述算法的有效性，固定股道状态，改变动车组的数目：取案例一、二的前3、4、5、6辆动车组的进出所时刻，分别用MIP-Solver、HEU算法对算例进行求解并对比。设定MIP-Solver求解的最大时间上限为3 h，MIP-Solver(有初始解)是将启发式算法求得的解赋值给MIP-Solver后再进行求解。当股道状态固定为I时，算法求解结果如表2所示。由表2可见，MIP-Solver在规定的时间内均找到了可行解，且案例一、二中的算例3、4、5为最优解，算例6在规定的时间内求得的目标值的Gap分别为为1.3%、2.0%，随着动车组数量的增加，MIP-Solver的求解时间逐渐变大；与之对比，HEU算法求解案例一、二中算例3、4、5的目标值与MIP-solver求解的目标值相同，而算例6中的目标值略低于MIP-Solver所求解的目标值，且HEU算法求解时间均在0.5 s以内。然后，将HEU算法的解带入MIP-Solver进行检验，与预想一致，将HEU算法所求初值赋予MIP-Solver会极大地减小求解空间，并快速地得到Gap为0且与HEU算法求解相同的目标值。

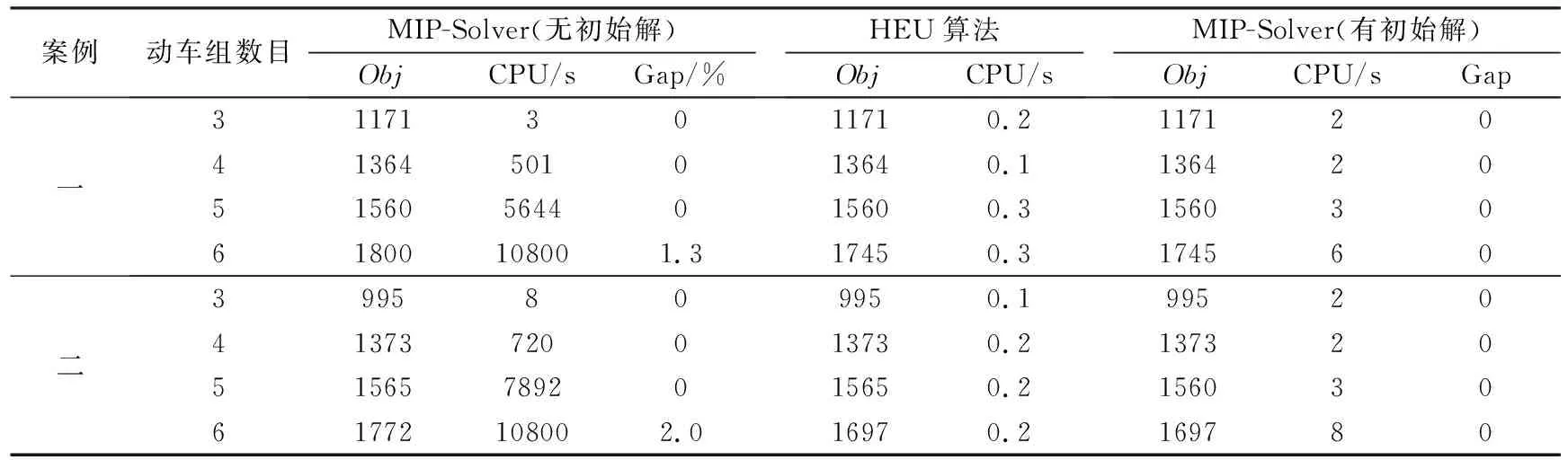
表2 算法求解结果Table 2 Algorithm solution results

图2所示为案例二的前6个动车组的调车作业计划求解结果Gantt图，横轴为时间轴，纵轴为股道编号。股道上绘制的长条表示动车组对相应股道的占用，长条的长度为股道占用时长。从图2中可以看出，股道资源均衡利用，且在清洗区和检修区完成作业时间均为标准作业时间。上述小规模对比试验结果证明了所提出算法的有效性。

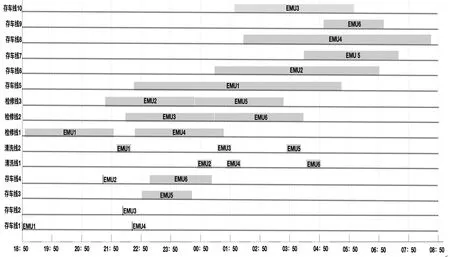
图2 动车所调车作业Gantt图Fig.2 Shunting schedule Gantt of EMU depot

4.2 启发式算法对比实验

将本文提出的启发式算法(HEU)与FCFS、EDD及STT等3种常见的启发式算法[8]进行对比分析，其中FCFS的基本思想为:先回到动车所的最先进行调度，且分配到最先空闲的车道上；EDD的基本思想为：最先离开动车所的车辆，具有最高优先权，且分配到最先空闲的车道上；STT的基本思想为：最短在库时间优先法则。计算每辆动车在动车所的停留时间(停留时间=出所时刻-入所时刻)，该时间最短的具有最高优先权，分配到最先空闲的车道上。

实验算例设置：动车组的数量分别取案例一和二中的前5、6、7、8辆；股道资源状态分别从I取到VIII共八种情形。从而可得，每个案例的算例规模为32个，两组案例共64个算例。为了验证算法的性能，采用偏移比DP[8]比较上述四种启发式算法在64个案例中的优越性。计算公式为

(17)

式中，Objbest为每个案例下，4种启发式算法求出的最好解的目标值，Objsol为每个启发式算法获取解的目标值。4种启发式算法在64个案例下的对比结果见表3。由表3对比分析可知，在计算时间无显著差异的情况下，HEU算法相较于另外3种常见的启发式算法，其解的质量在所有案例中均是最优的。

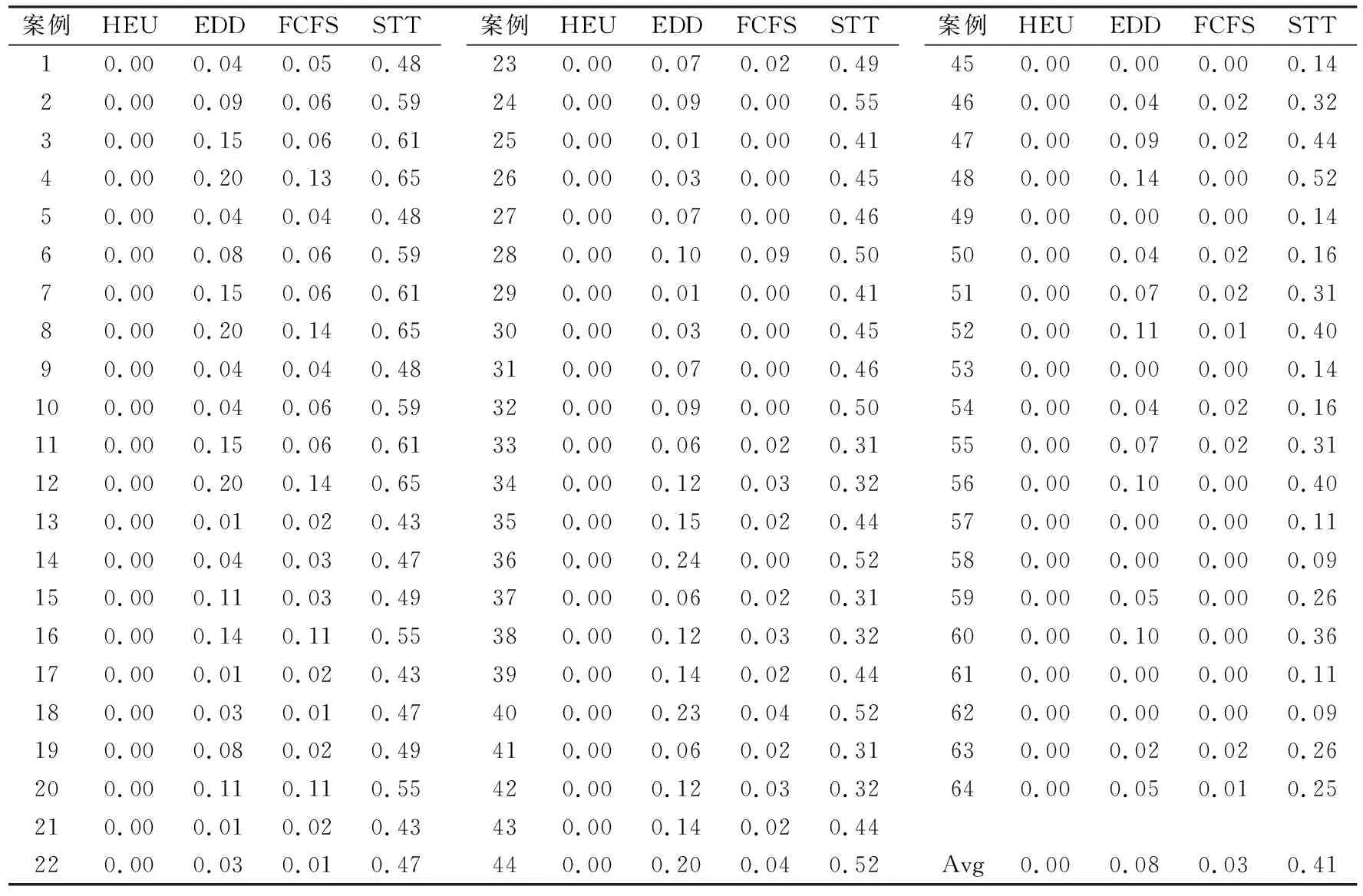
表3 算法结果对比Table 3 Algorithms solution comparison

5 结语

为了有效、快速地实现调车作业计划编制与优化，构建了动车所调车作业计划编制与优化的混合整数规划模型，并描述了模型的约束和目标。在模型的基础上，设计了基于“先进先服务”“股道均衡分配”“股道占用时间最小化”规则的启发式求解算法。在实验算例中，对本文所提出的启发式算法求解结果与精确的MIP算法求解结果进行比较，验证该启发式算法的可行性和求解效率，此外，又将其与调度中常见的3类启发式算法进行了比较，结果表明，本文所提的启发式算法求解结果具有明显的优越性。在未来的工作中，更多符合实际现场的因素应予考虑，例如动车组的长短编之分，股道之间的瓶颈冲突等，在本文所提出的启发式算法基础上可设计出更优化的算法对实际问题进行求解。