可变节流面积气浮支承静态性能仿真研究

李 双，孔建益，于普良，胡江山

(1. 武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉 430081;2. 武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉 430081;3. 武汉科技大学精密制造研究院，湖北 武汉， 430081)

气浮支承具有精度高、速度快、无摩擦、零污染等优良特性，契合了精密及超精密制造的特殊要求，但气体的可压缩特性导致其刚度与承载力等静态性能指标偏低[1-3]。为了有效提高气浮支承的刚度与承载力，气浮支承的节流方式作为影响其静态性能的重要因素受到了众多研究者的关注，Stiffler[4]研究了节流孔数量对气浮支承静态性能的影响；Boeffy等[5]和Kassab等[6-7]通过实验研究了节流孔结构参数和供气压力与静压止推轴承静态性能之间的关系；Rowe等[8]基于精确的有限差分技术，提出了狭缝节流气体径向轴承的静态性能计算方法，揭示了气浮轴承的安全加载极限且同时给出了单排和双排构型条件下的计算结果；王仁宗等[9]利用fluent仿真研究了狭缝尺寸参数及数量对轴承承载力和刚度的影响规律；本课题组[10-11]以及Chen等[12-13]通过增加气浮支承表面微织构的方式来提高气浮支承静态特性，获得了较理想的研究结果。综上所述，已有的相关报道大多涉及固有节流器，而针对可变节流器的研究相对较少，为此本文设计了一种具有可变节流面积的空气静压气浮支承，利用柔性机构的挠度变形实现径向狭缝高度Hb的变化以改变节流面积，从而提高气浮支承的承载力与刚度，并通过所建立的可变节流面积气浮支承计算流体动力学(CFD)模型，分析了径向狭缝高度、轴向狭缝宽度、均压腔深度和供气压力对气浮支承承载力和刚度的影响。

1 CFD仿真

1.1 可变节流面积静压气浮支承结构模型

可变节流面积气浮支承结构及主要参数分别如图1和表1所示，其中供气压力Ps取值分别为0.2、0.3、0.4、0.5、0.6 MPa，出气口压力P0为0.1 MPa。由图1可见，气浮支承结构主体由上端盖、柔性机构和下支承等部分构成，该结构的节流面积变化示意图见图2。图2中，F作用力方向与气浮支承工作面垂直，当F方向向上时记为“F>0”，当F方向向下时记为“F<0”。通过施加在柔性机构上作用力F，可以改变其径向狭缝高度Hb，因为气浮支承节流面积S=πD3Hb，故通过改变径向狭缝高度Hb可以间接改变节流面积的大小，节流面积的变化又直接影响其气体流量，从而能达到调节气浮支承静态特性的目的。

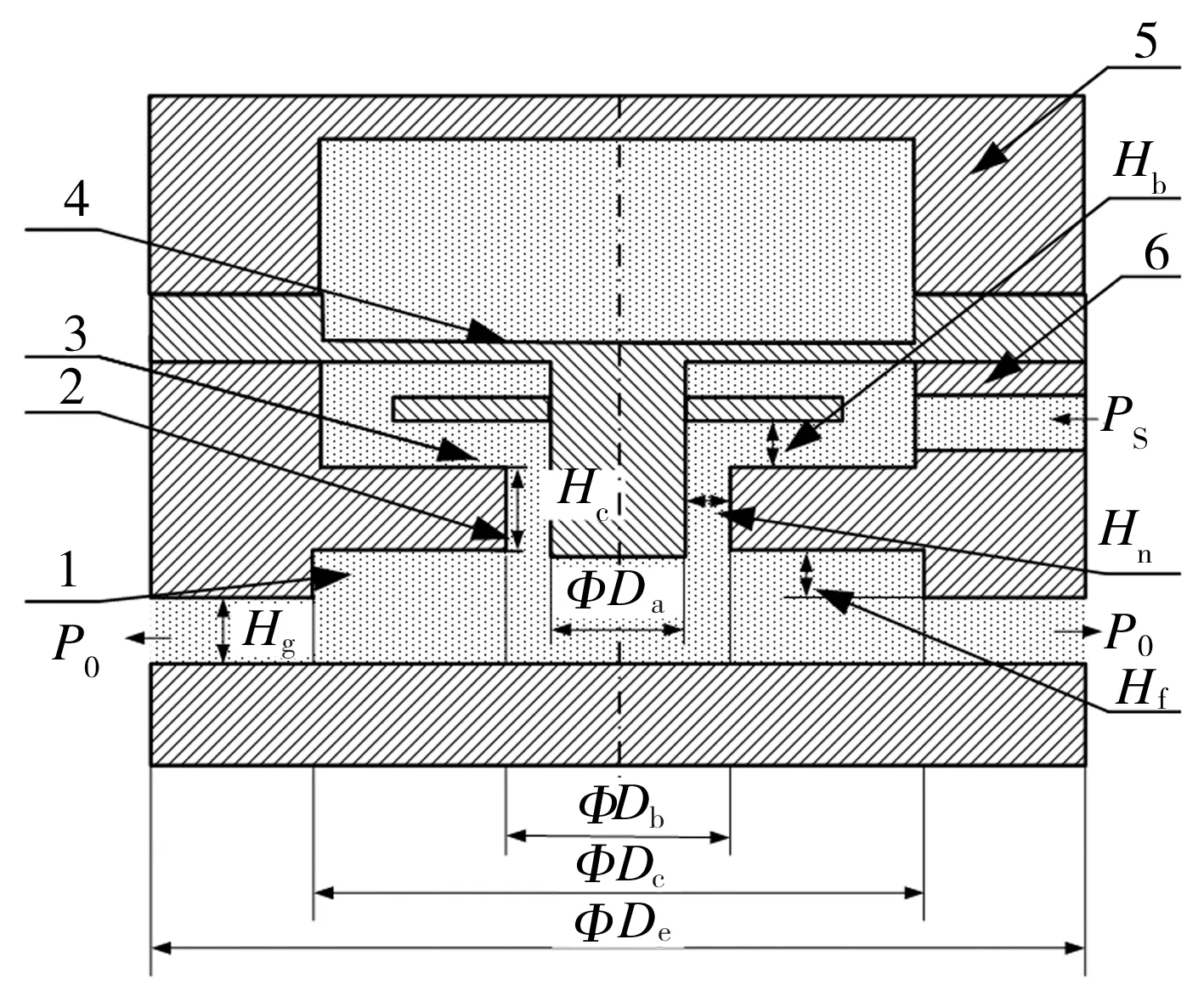
1—均压腔;2—轴向狭缝;3—径向狭缝;4—柔性铰链;5—上端盖;6—下支承(a)整体图

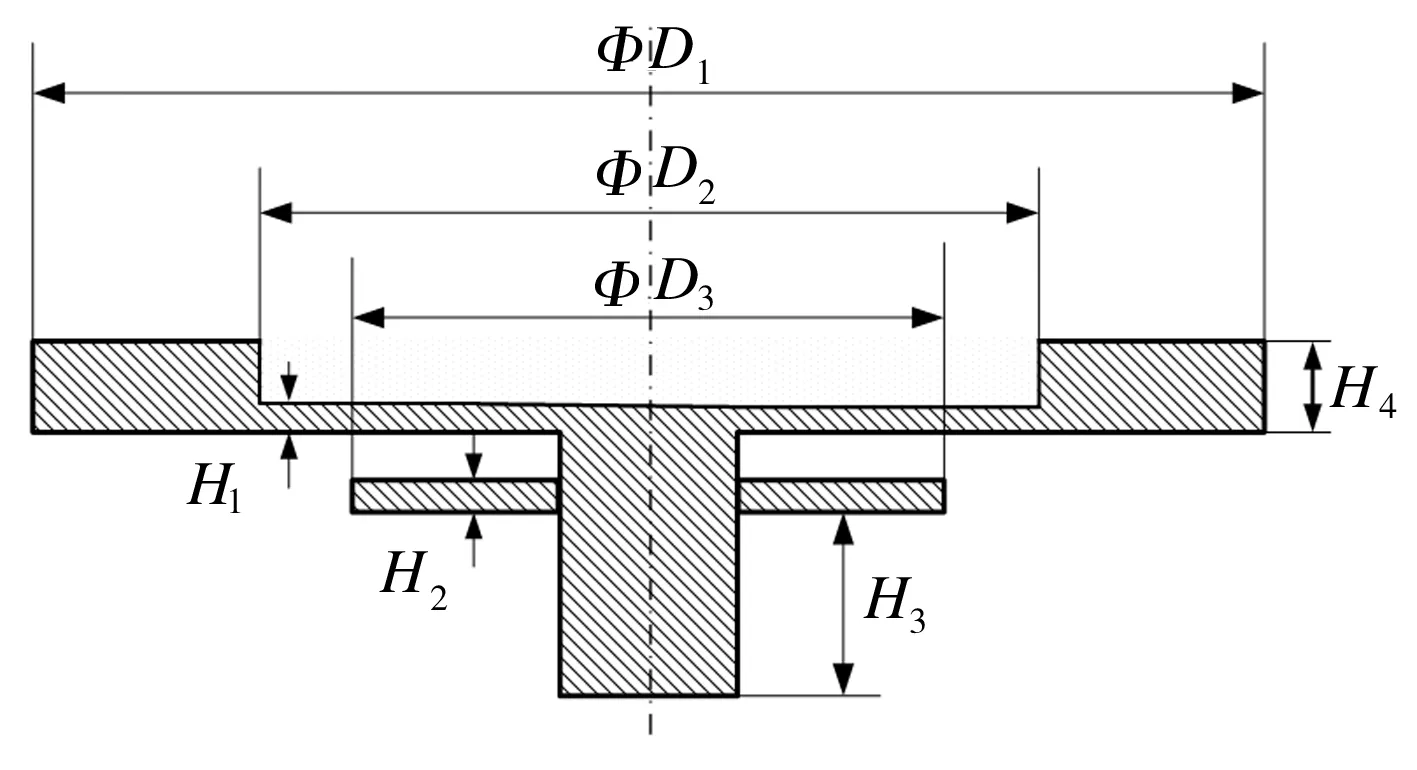
(b)局部图(柔性铰链部分)图1 可变节流面积气浮支承系统结构剖视图Fig.1 Sectional view of aerostatic bearing with variable-throttling areas

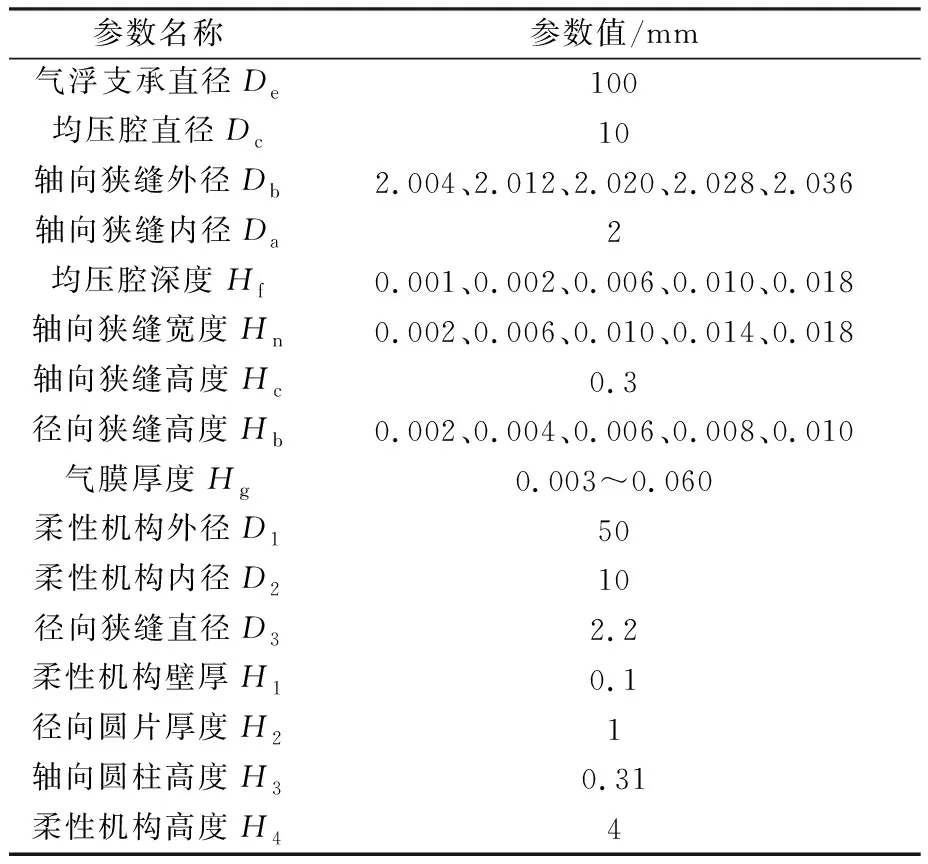
表1 主要结构参数Table 1 Main structural parameters

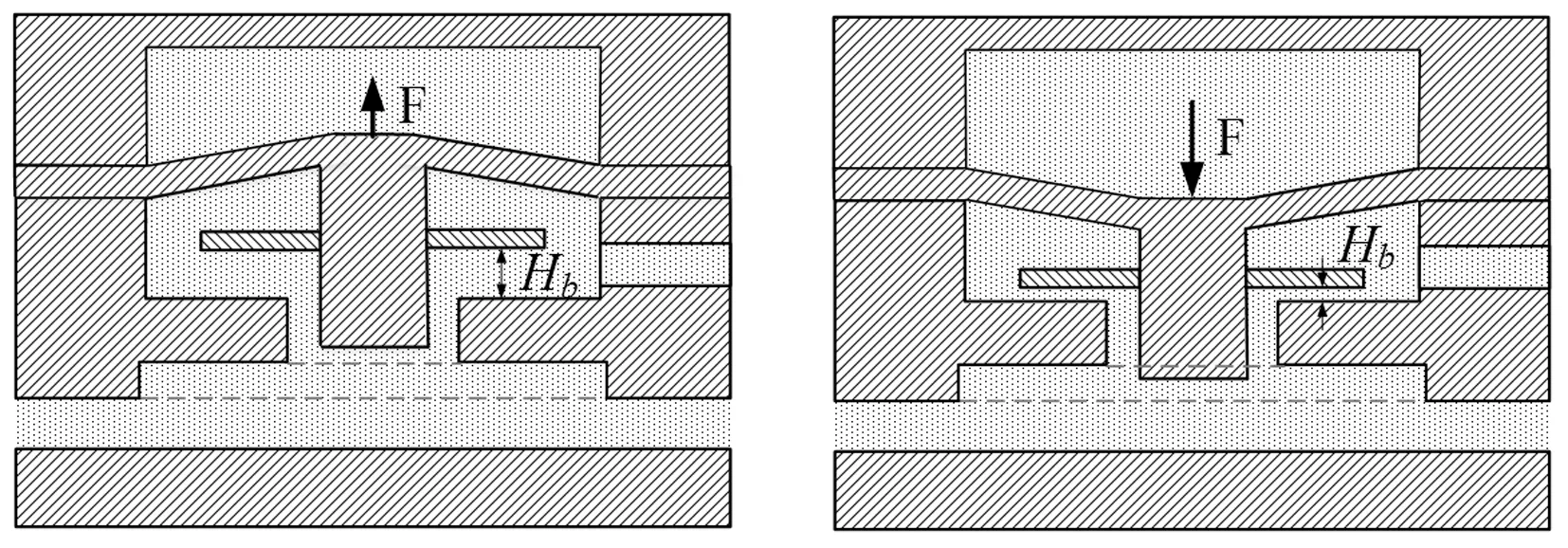
(a)F>0，Hb增大 (b)F<0，Hb减小图2 节流面积变化示意图Fig.2 Variation diagrams of throttling areas

1.2 气体润滑控制方程

为构建气体在气浮支承内的流动模型及求解气浮支承的承载力和刚度，需建立如下假设：(1)气膜膜厚方向上的压力不变；(2)不考虑气体体积力和惯性力的影响；(3)气体为牛顿流体；(4)气体在流动过程中与气浮支承各结构均无热量交换。基于以上假设，依据流体三大基本方程和气体状态方程可得到气体静压润滑雷诺方程的一般表达式[14]为

(1)

式中，x和z分别为垂直气膜厚度方向及气膜厚度方向的位移；ρ为气体密度；p为气膜压力;u1和u2分别为气体在气浮支承上表面及下表面的运动速度；μ为气体动力黏度；t为时间。气浮支承的承载力W为

(2)

式中，A为气浮支承工作面面积。气浮支承的刚度K为

(3)

1.3 网格划分与计算条件设置

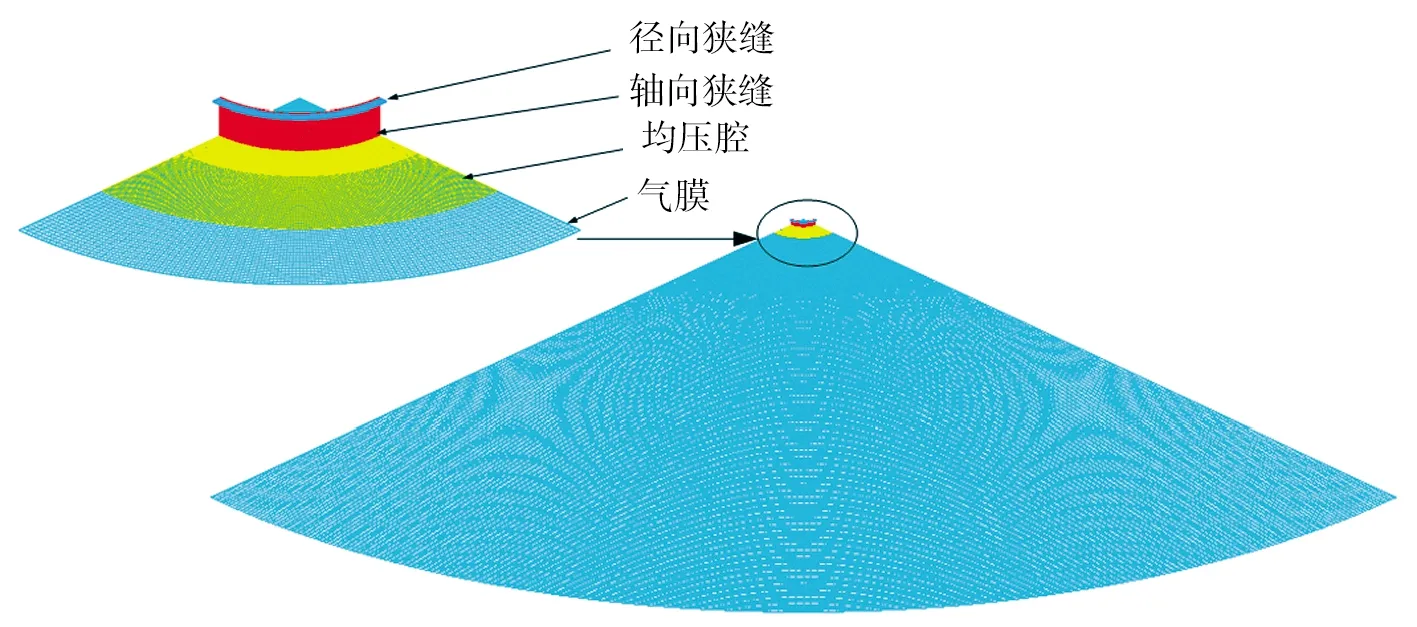
图3 气浮支承CFD模型Fig.3 CFD model of aerostatic bearing

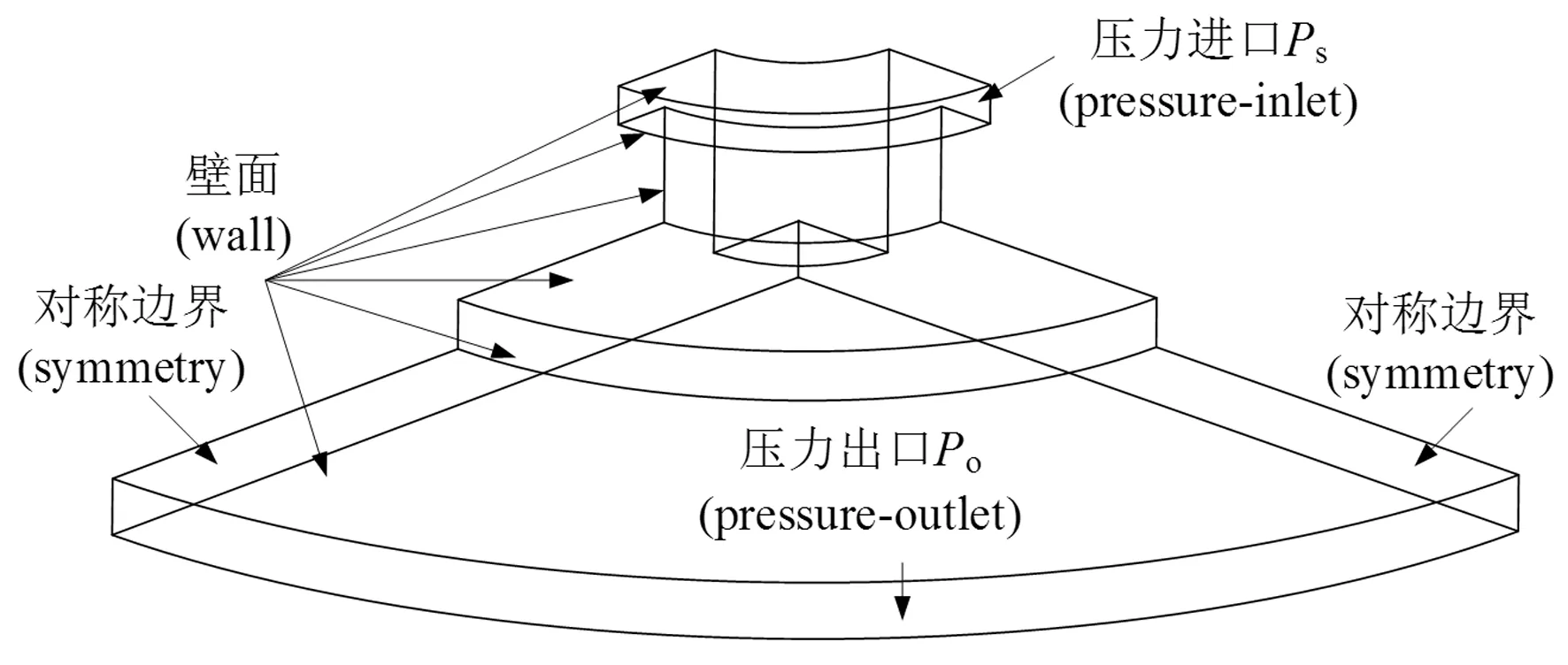
图4 气浮支承边界条件Fig.4 Boundary conditions of aerostatic bearing

1.4 仿真分析方法适用性验证

为验证本研究中气浮支承静态性能计算方法的可行性，采用于贺春等[15]设计的气浮支承，将基于本研究仿真方法所得结果与其试验数据进行对比分析，图5所示为文献[15]中的气浮支承结构，其中进气口压力Ps为0.6 MPa，出气口压力P0为0.1 MPa，相关结构参数见表2，借助本研究所用数值模拟方法获得该气浮支承在不同气膜厚度条件下的承载力仿真数据与文献[15]中相应的试验数据对比分析结果如图6所示。由图6可见，通过基于标准k-ε湍流模型数值仿真方法所得结果与文献[15]试验所得结果在试验允许误差范围内吻合度较高，证明了本研究所用基于k-ε湍流模型的数值仿真方法对气浮支承静态特性进行计算的可操作性较强、准确度较高。

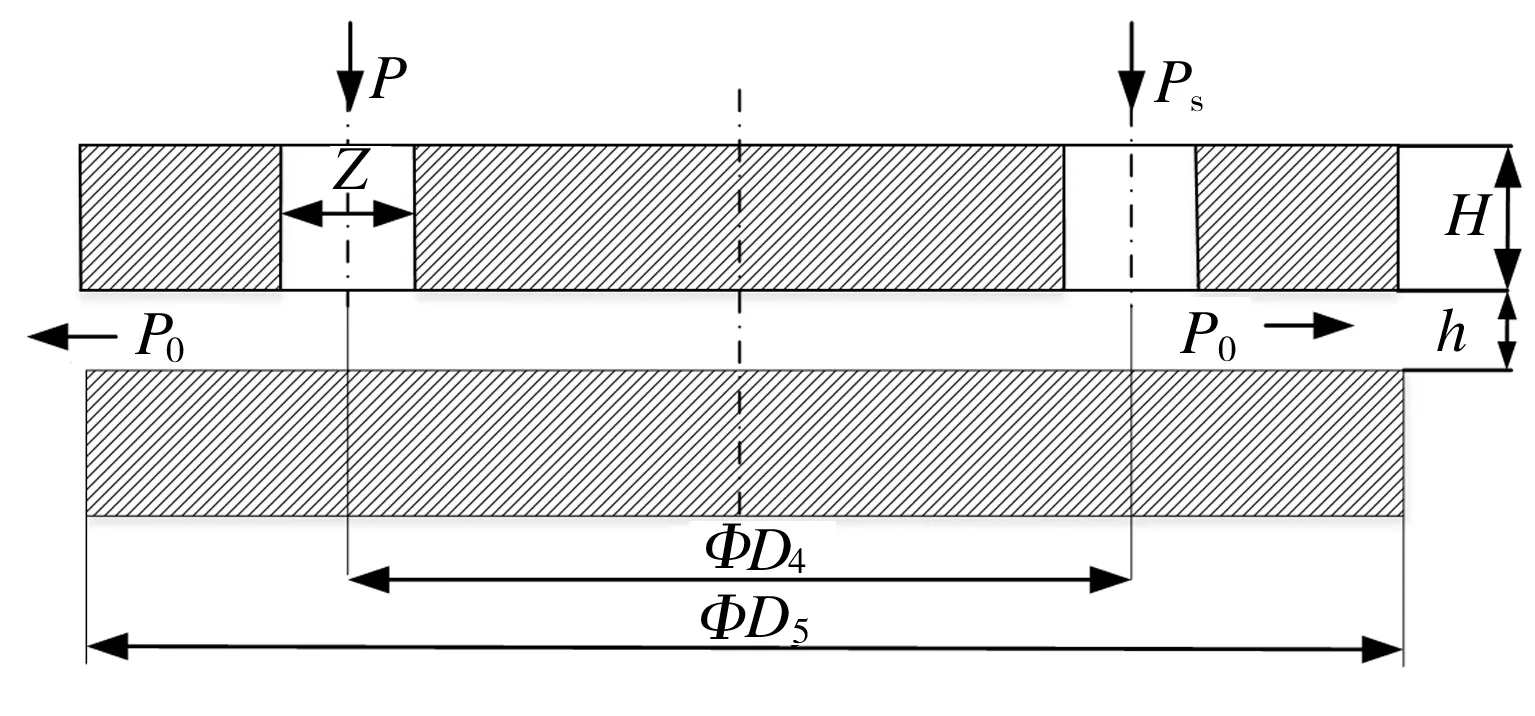
图5 气体静压止推轴承结构示意图Fig.5 Structural diagram of aerostatic thrust bearing

表2 气体静压止推轴承主要结构参数Table2 Main structural parameters of aerostatic thrust bearing

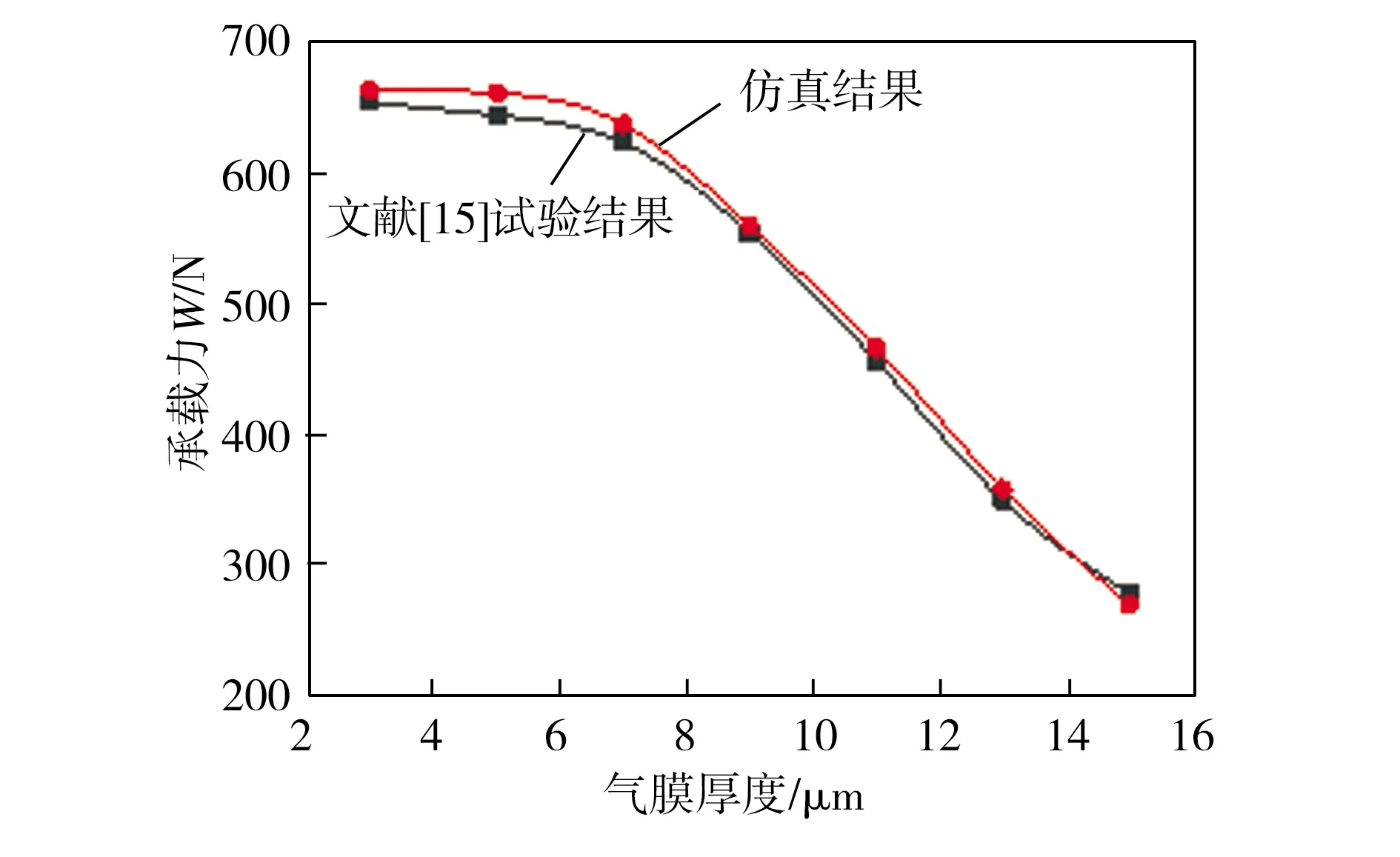
图6 试验与仿真结果对比Fig.6 Comparison of experimental and simulation results

2 仿真结果及分析

2.1 压强分布

基于表1所示气浮支承各项结构参数，其中径向狭缝高度Hb分别取0.002、0.004、0.006、0.008、0.010 mm，轴向狭缝宽度Hn取0.018 mm，均压腔深度Hf取0.018 mm、气膜厚度Hg取0.010 mm、供气压力Ps取0.6 MPa，外界环境压力P0取0.1 MPa，按前文所述网格划分及计算条件(1.3节)，计算所得气浮支承压强云图如图7所示，不同径向狭缝高度下，同一位置同一气膜厚度处气浮支承径向直线压强分布对比图见图8，由于气膜厚度方向上压强处处相等，故对该径向直线的具体位置可以不作要求。由图7和图8可知，增加气浮支承径向狭缝高度能增强其气膜内部以及径向直线上的压强分布，因此气浮支承节流面积的增大可有效增大其承载力。

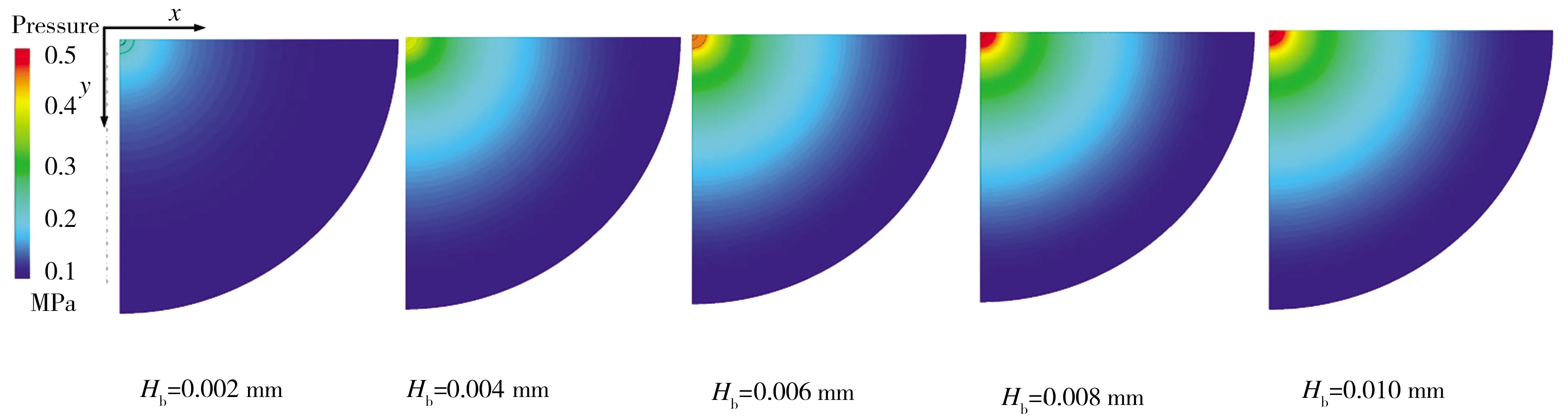
图7 压强云图Fig.7 Pressure nephogram

2.2 径向狭缝高度Hb对气浮支承静态性能的影响

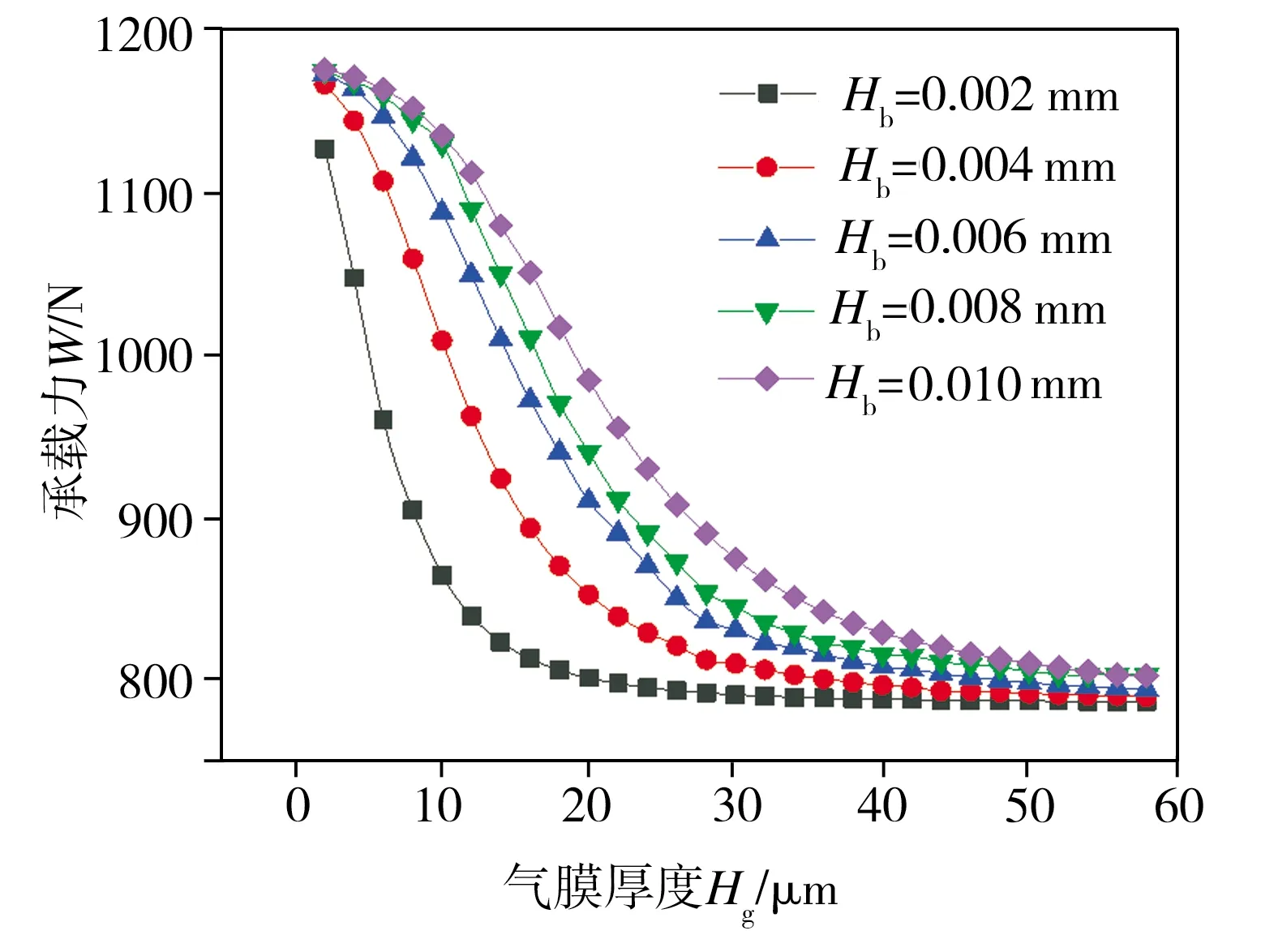
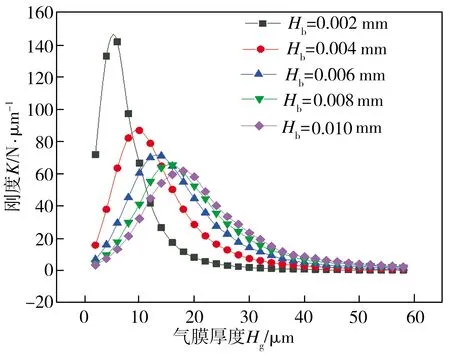
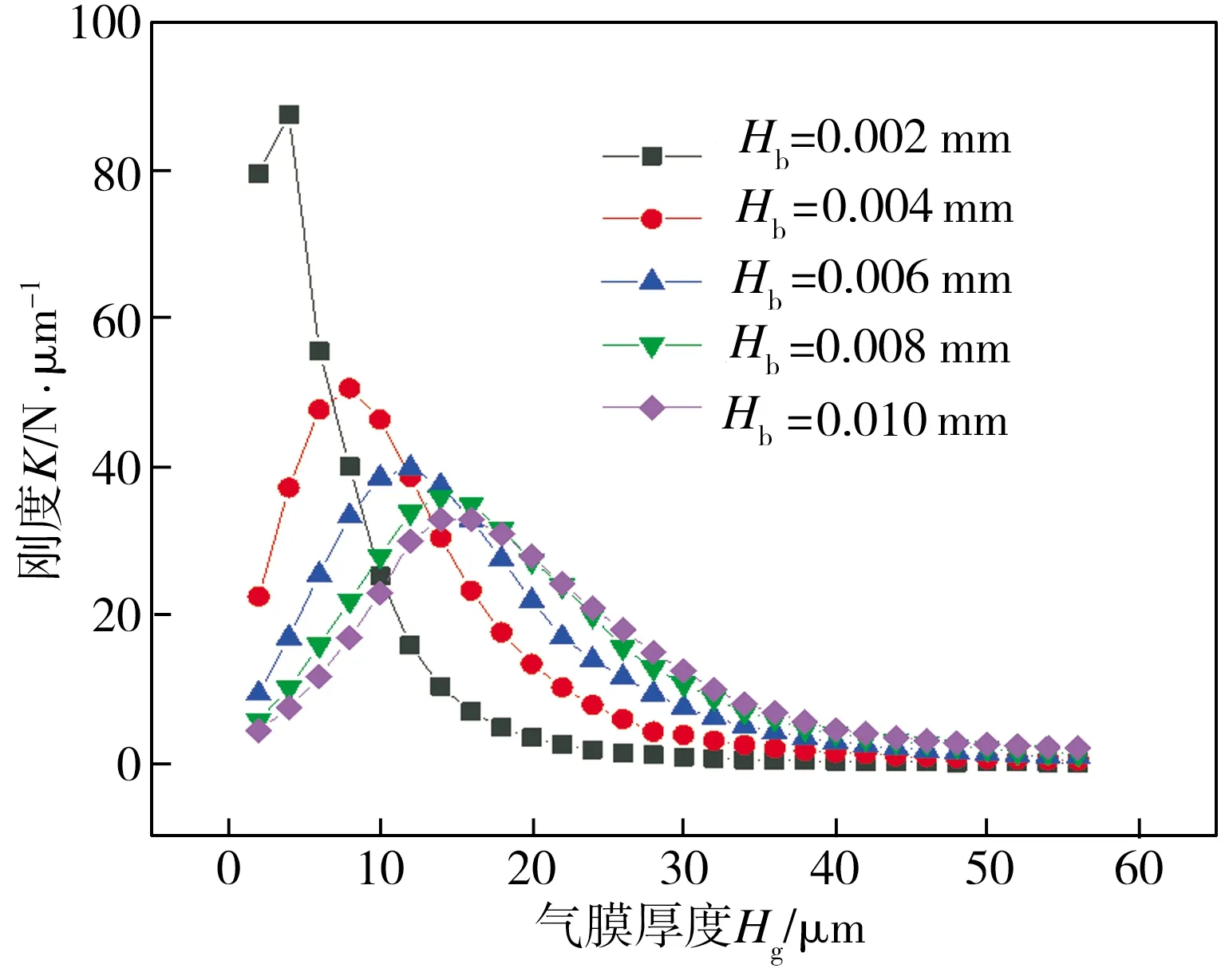
设定可变节流面积气浮支承的Hn为0.018 mm、Hf为0.018 mm，在其余结构参数一定的条件下，研究了供气压力Ps分别为0.2、0.4、0.6 MPa时，气浮支承径向狭缝高度Hb的变化对其承载力及刚度的影响，仿真结果分别见图9和图10。由图9可知，当气浮支承供气压力恒定时，在不同的径向狭缝高度条件下，增大气膜厚度均会导致气浮支承承载力逐渐减小且趋近于某一稳定值；在相同气膜厚度条件下，气浮支承径向狭缝高度的增大会导致其承载力增大。从图10中可见，当气浮支承供气压力恒定时，在不同的径向狭缝高度下，气浮支承刚度均随着气膜厚度的增加先增大至某一峰值后再逐渐减小直至趋近于0，此外，随着径向狭缝高度的增大，气浮支承刚度峰值逐渐降低且降幅不断减小，而刚度峰值相对应的气膜厚度却逐渐增加且增幅逐渐减小。综上所述，当供气压力恒定时，增加可变节流面积气浮支承的径向狭缝高度虽能提高其承载力，但不能同时增大其刚度峰值，基于仿真分析结果，当Hb约为0.006 mm时,气浮支承同时具有较高的承载力与刚度。

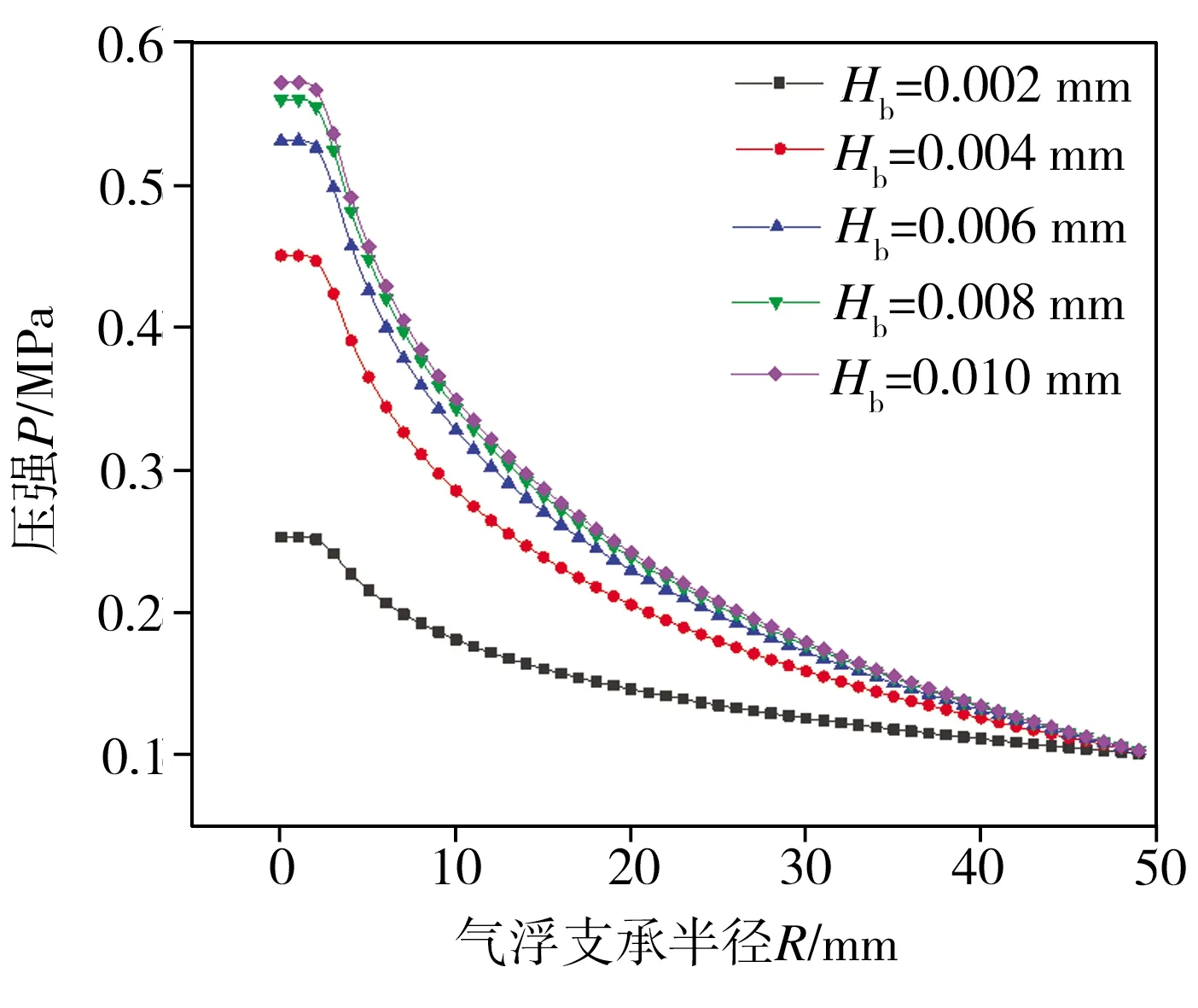
图8 径向压强对比曲线Fig.8 Radial pressure comparison curves

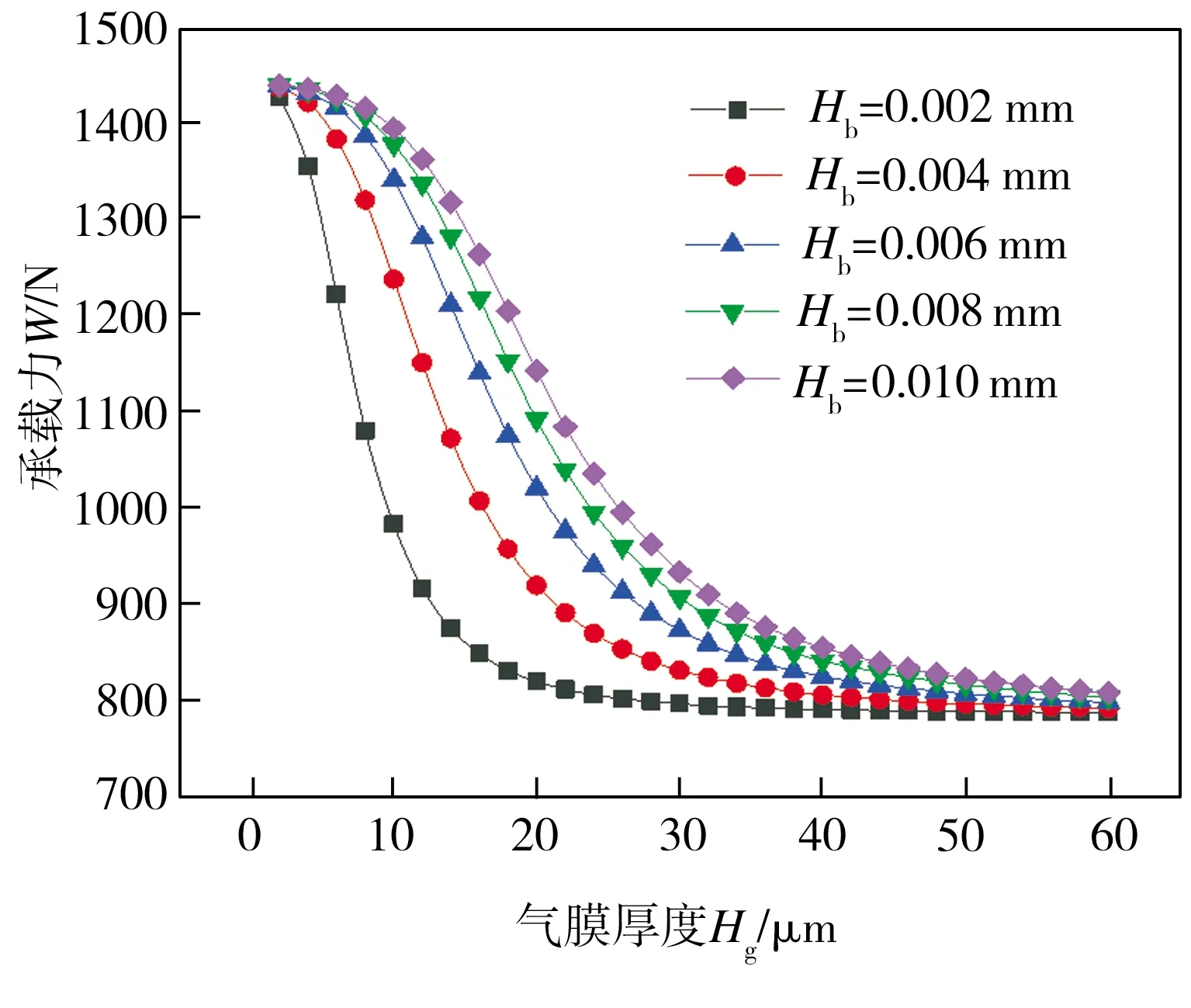
(a) Ps=0.6 MPa

(b) Ps=0.4 MPa

(c) Ps=0.2 MPa图9 不同径向狭缝高度条件下气浮支承承载力随气膜厚度的变化Fig.9 Variation of aerostatic bearing bearing capacities with gas film thicknesses under various radial slit heights

(a) Ps=0.6 MPa

(b) Ps=0.4 MPa

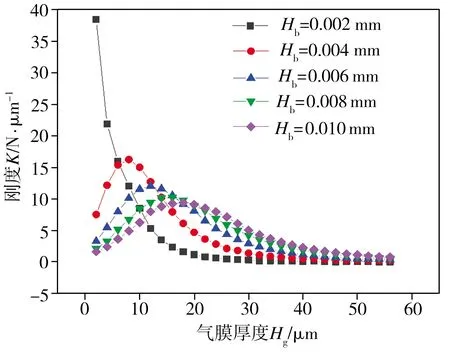
(c) Ps=0.2 MPa图10 不同径向狭缝高度条件下气浮支承刚度随气膜厚度的变化Fig.10 Variation of aerostatic bearing stiffnesses with gas film thicknesses under various radial slit heights

2.3 轴向狭缝宽度Hn对气浮支承静态性能的影响

设定可变节流面积气浮支承的Hb为0.010 mm、Hf为0.018 mm，Ps为0.6 MPa，在其它结构参数一定的情况下，研究了气浮支承轴向狭缝宽度Hn的变化对其承载力及刚度的影响，仿真结果分别见图11和图12。由图11可见，在不同的轴向狭缝宽度条件下，气浮支承承载力均随气膜厚度的增加而减小并逐渐趋近于某一稳定值；在气膜厚度相同的条件下，气浮支承承载力随其轴向狭缝宽度的增加而增大。从图12中可以看出，在不同的轴向狭缝宽度条件下，气浮支承刚度均随着气膜厚度的增加先迅速增大至某一峰值后再逐渐减小直至趋近于0，且随着轴向狭缝宽度的增加，气浮支承刚度峰值明显降低，而峰值所对应的气膜厚度却相应增加。综上所述，增大可变节流面积气浮支承轴向狭缝宽度可有效提高其承载力，但不能同时提高其刚度峰值，根据仿真分析结果，当Hn约为0.010 mm时，可保证气浮支承同时具有较高的承载力与刚度。

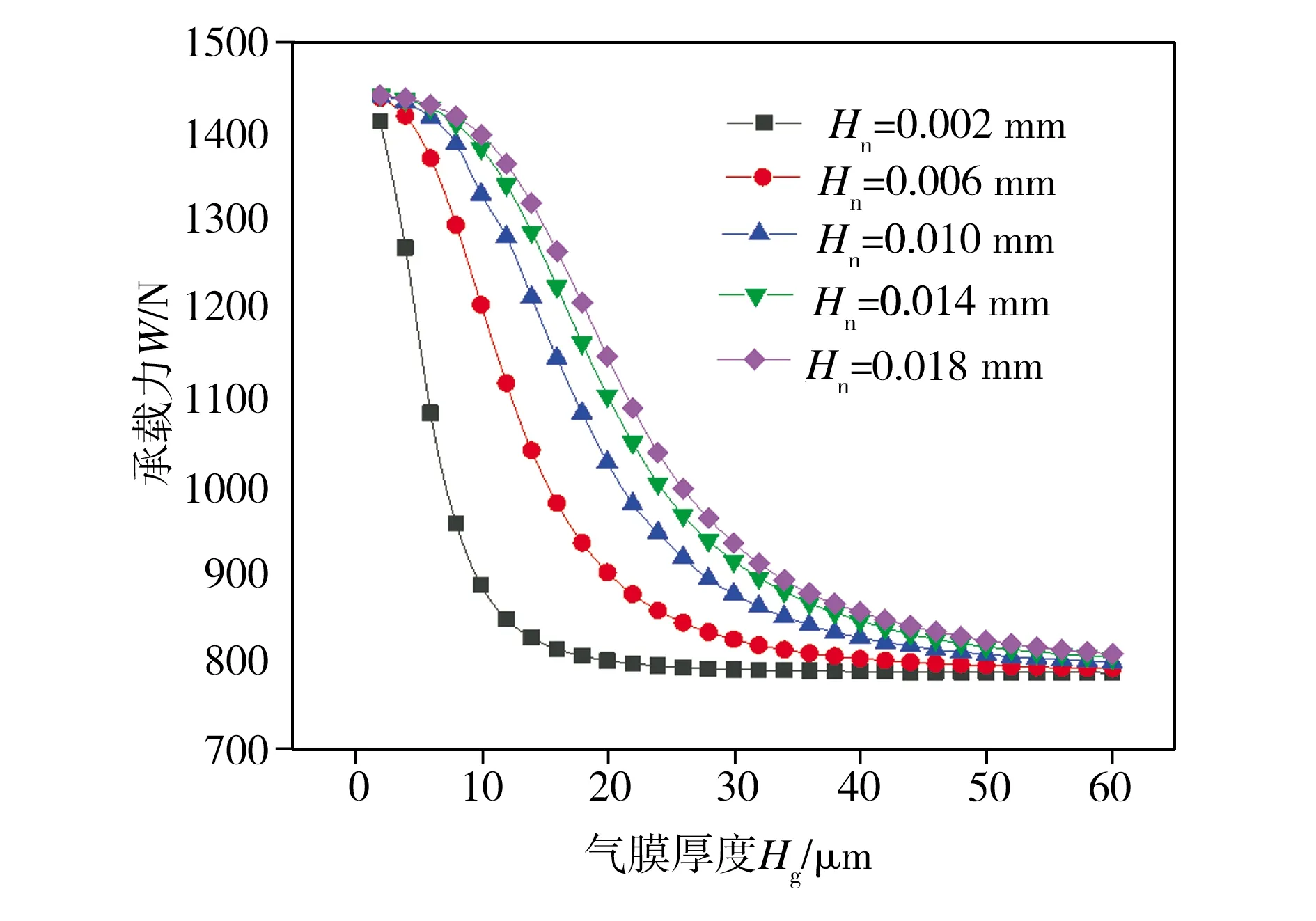
图11 不同轴向狭缝宽度条件下气浮支承承载力随气膜厚度的变化Fig 11 Variation of aerostatic bearing bearing capacities with gas film thicknesses under various axial slit widths

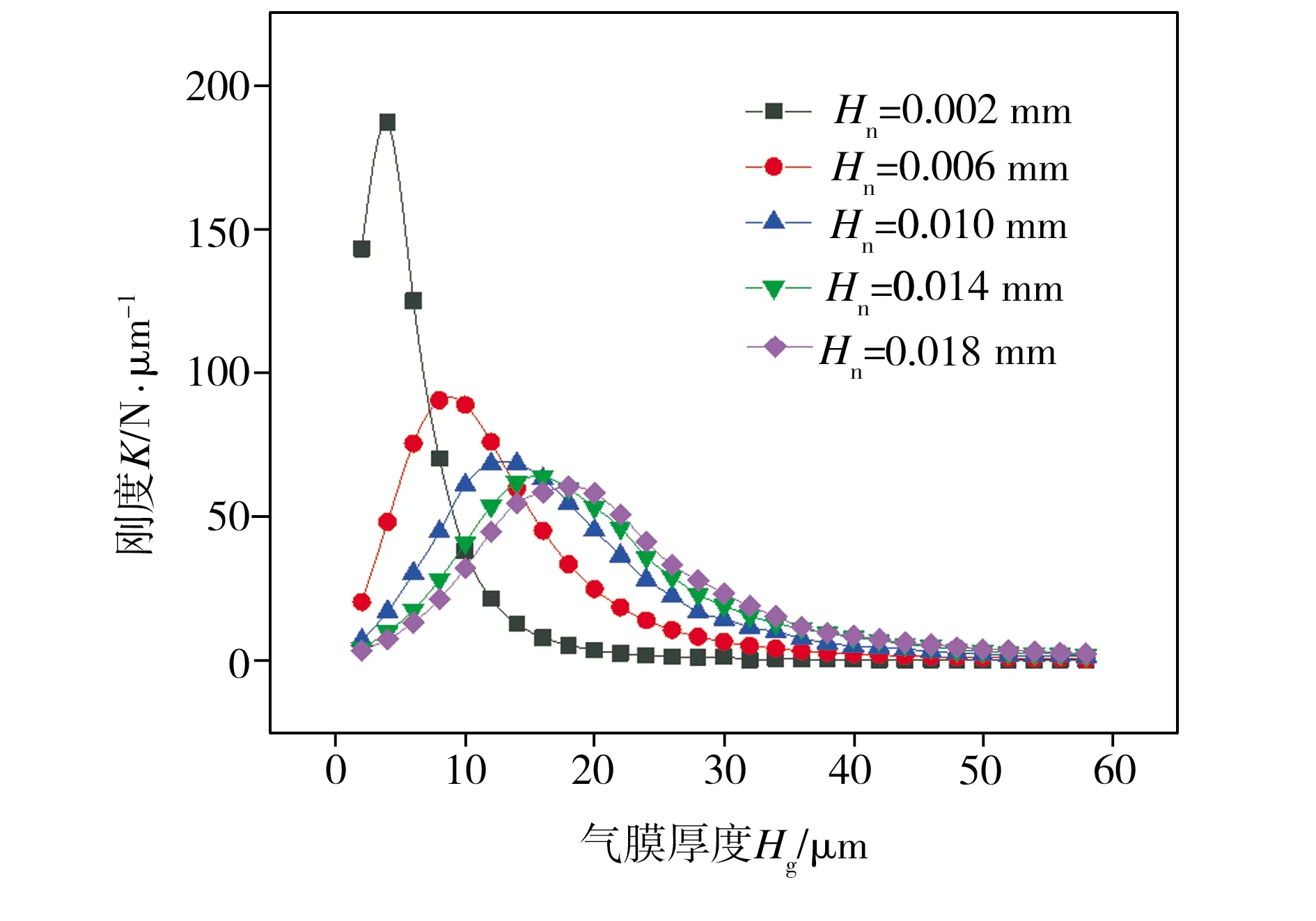
图12 不同轴向狭缝宽度条件下气浮支承刚度随气膜厚度的变化Fig.12 Variation of aerostatic bearing stiffnesses with gas film thicknesses under various axial slit widths

2.4 均压腔深度Hf对气浮支承静态性能的影响

设定可变节流面积气浮支承的Hn为0.018 mm、Hb为0.010 mm、Ps为0.6 MPa，在其它结构参数一定的情况下，研究了气浮支承均压腔深度Hf的变化对其承载力及刚度的影响，仿真结果分别见图13和图14。由图13可见，在不同的均压腔深度条件下，增大气膜厚度均会导致气浮支承承载力迅速减小并趋近于某一稳定值，当气膜厚度不变且小于18 μm时，增大均压腔深度能在一定程度上提升气浮支承承载力。从图14可以看出，在不同的均压腔深度条件下，气浮支承刚度均随气膜厚度的增加先增大至某一峰值后再逐渐减小直至趋近于0，且刚度峰值随均压腔深度的增加而增大，此外，不同均压腔深度条件下的气浮支承刚度峰值所对应的气膜厚度均为18 μm左右。分析结果表明，均压腔深度的增大虽然可以提高气浮支承刚度峰值，但对其承载力影响不大，当Hf约为0.018 mm时，气浮支承同时具有较高承载力与刚度。

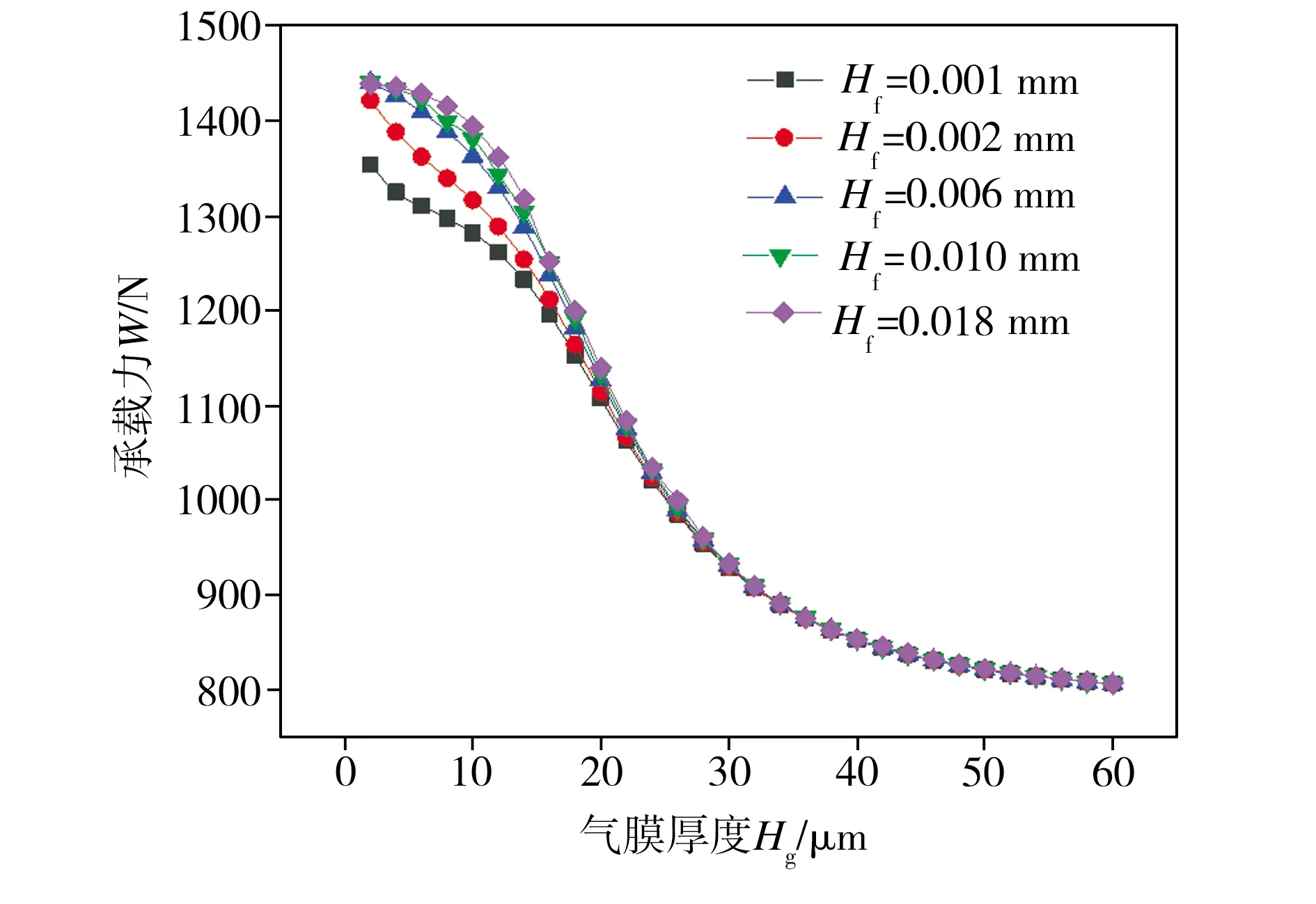
图13 不同均压腔深度条件下气浮支承承载力随气膜厚度的变化Fig.13 Variation of aerostatic bearing bearing capacities with gas film thicknesses under various chamber depths

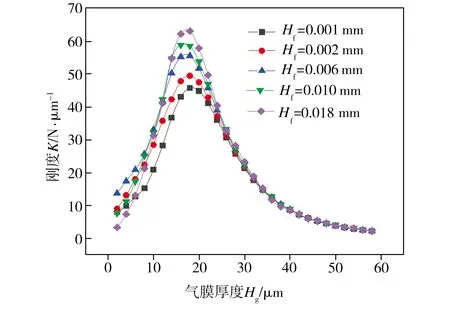
图14 不同均压腔深度条件下气浮支承刚度随气膜厚度的变化Fig.14 Variation of aerostatic bearing stiffnesses with gas film thicknesses under various chamber depths

2.5 供气压力Ps对气浮支承静态性能的影响

设定可变节流面积气浮支承的Hn为0.018 mm、Hb为0.010 mm、Hf为0.018 mm，在其它结构参数一定的情况下，研究了气浮支承供气压力Ps的变化对其静态特性影响，仿真结果分别见图15和图16。由图15可见，在不同的供气压力条件下，增大气膜厚度均会导致气浮支承承载力先迅速减小而后又降幅趋缓，直至达到某一稳定值，此外，当气膜厚度不变且小于18 μm时，不同供气压力条件下气浮支承承载力值的变化较明显。从图16中可以看出，在相同供气压力条件下，气浮支承刚度均随气膜厚度的增大而增至某一峰值后再逐渐减小直至趋近于0，且气浮支承刚度峰值对应的气膜厚度不随供气压力的变化而变化，基本维持在18 μm左右。综合分析表明，增大可变节流面积气浮支承的供气压力可以同时提高其承载力和刚度峰值，当供气压力为0.6 MPa时，气浮支承同时具有高的承载力与刚度。

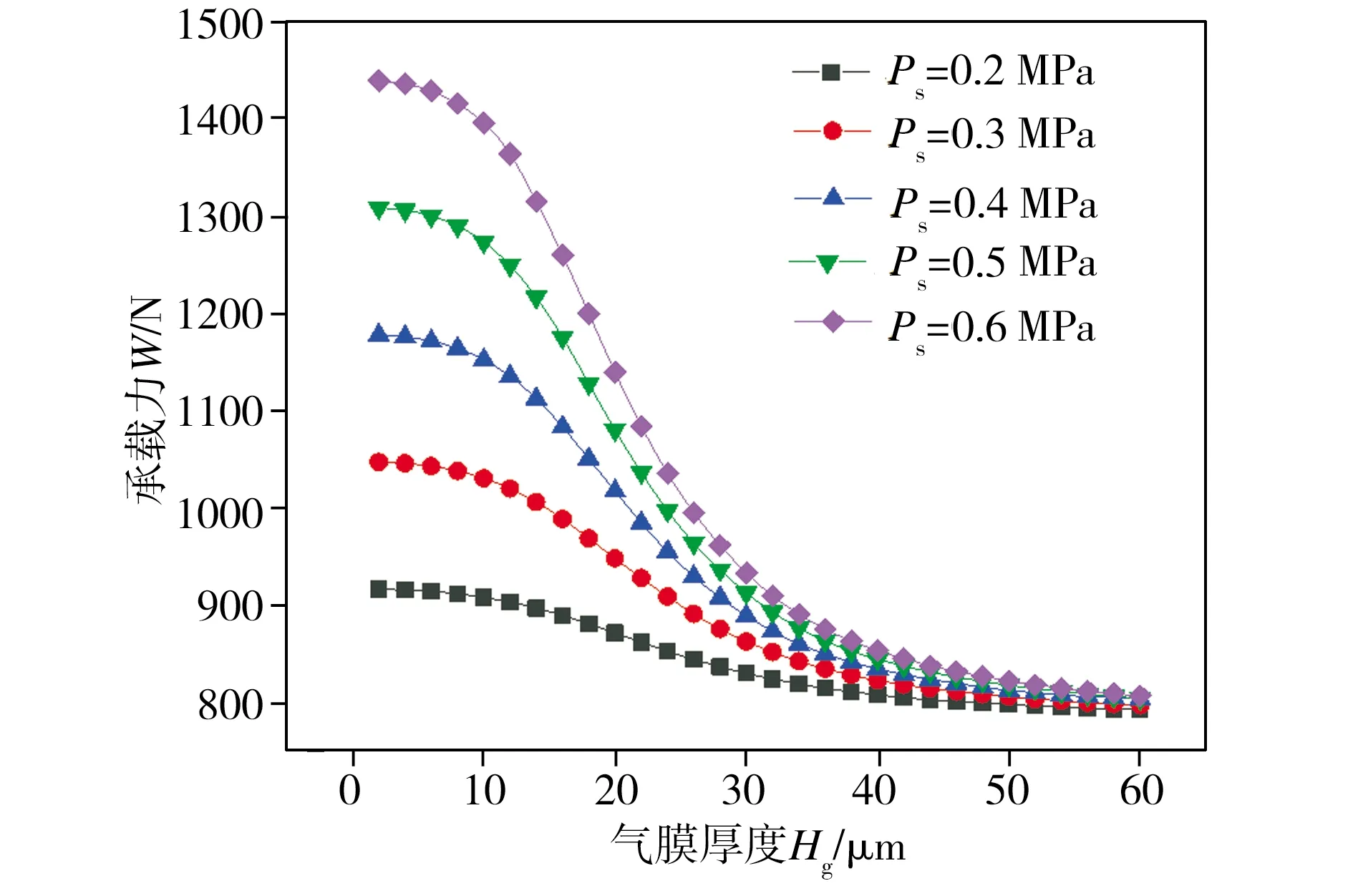
图15 不同供气压力条件下气浮支承承载力随气膜厚度的变化Fig.15 Variation of aerostatic bearing bearing capacities with gas film thicknesses under different supply pressures

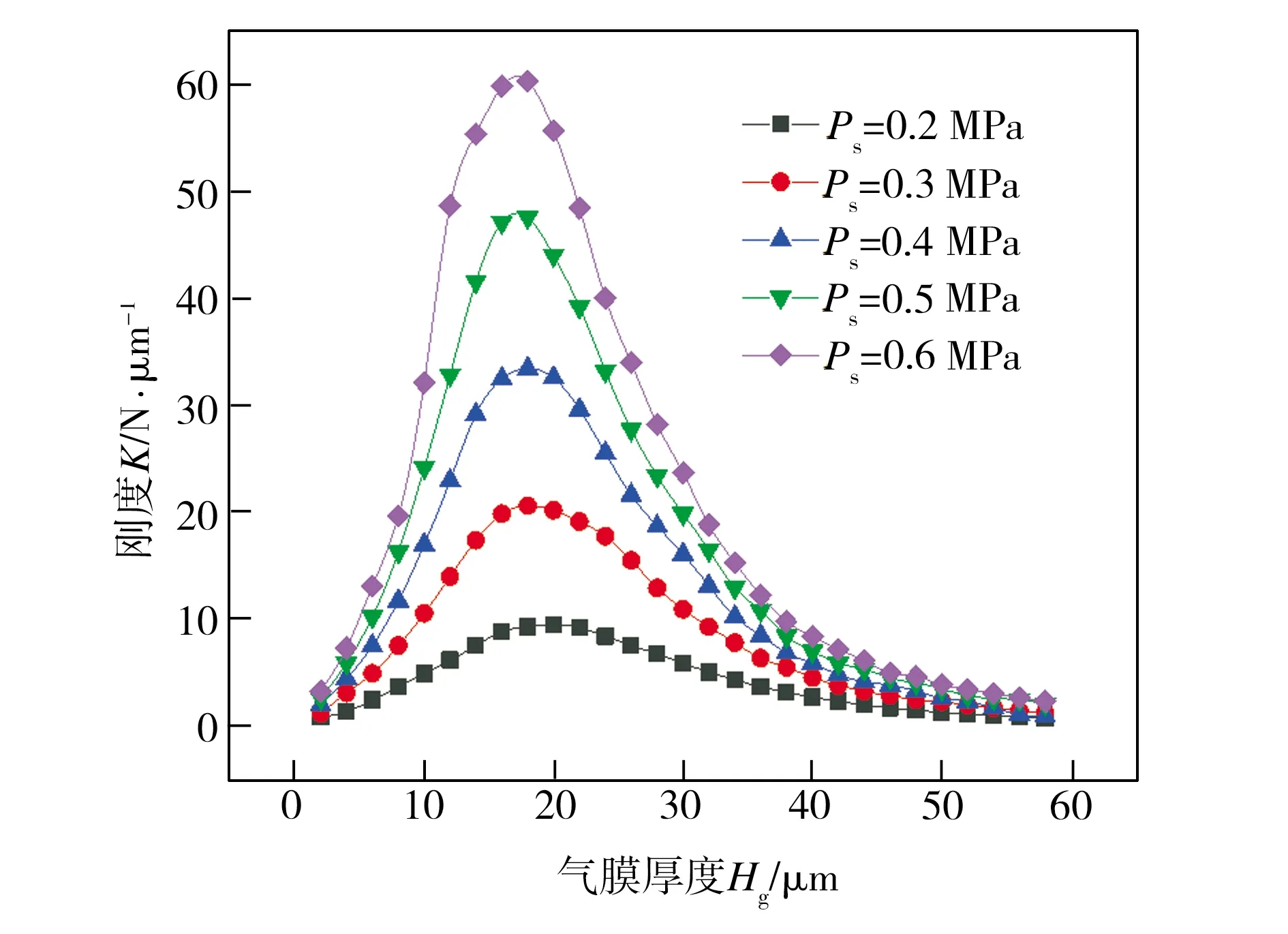
图16 不同供气压力条件下气浮支承刚度随气膜厚度的变化Fig.16 Variation of aerostatic bearing stiffnesses with gas film thicknesses under different supply pressures

3 结论

(1) 在其它参数一定的情况下，增大气浮支承径向狭缝高度Hb虽然可以提高其承载力，但不能提高其刚度峰值，当Hb约为0.006 mm时，气浮支承同时具有较高的承载力与刚度。

(2) 在其它参数一定的情况下，增大气浮支承轴向狭缝宽度Hn可以提高其承载力，但不能提高其刚度峰值，当Hn约为0.010 mm时，气浮支承同时具有较高的承载力与刚度。

(3) 在其它参数一定的情况下，增大气浮支承均压腔深度Hf可以提高其刚度峰值但对其承载力影响不大，且刚度峰值对应的气膜厚度稳定在18 μm左右，当Hf约为0.018 mm时，气浮支承同时具有较高的承载力和刚度。

(4) 在其它参数一定的情况下，增大气浮支承的供气压力Ps可以大幅度提高其承载力与刚度峰值，且刚度峰值对应的气膜厚度稳定在18 μm左右，当Ps为0.6 MPa时，气浮支承同时具有高的承载力和刚度。