铸坯质量缺陷预测的特征降维方法研究

李文深，容芷君，但斌斌

(1. 武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2. 武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081)

连铸生产过程中，及时在线预报和检测铸坯质量，对于确保生产连续性、提高产品质量以及降低生产成本具有重要意义[1]。当前对铸坯质量预测的研究主要有专家系统、专家系统与智能算法结合、数据挖掘等方法，随着大数据技术的发展，基于数据挖掘技术进行铸坯质量预测成为研究热点[1-2]。

数据挖掘通过提取影响铸坯质量的各类因素，将之作为模型的输入特征，利用机器学习算法找到输入特征与铸坯质量之间的映射关系，进而输出铸坯质量缺陷的预测结果。当前，针对铸坯质量缺陷问题的数据挖掘，多数研究首先根据冶金原理分析铸坯质量缺陷的影响因素，将其作为模型输入特征，然后利用神经网络[3]、随机森林[4]、模糊模式识别[5]等算法来实现铸坯质量缺陷预测，研究重点在于铸坯质量缺陷预测模型算法的选择与改进，而关于对模型输入特征处理的研究还不多见。虽然，基于冶金原理的研究方法保证了特征集中包含用于预测的所有重要信息，但炼钢是一个工序复杂、过程周期长、冷热变化剧烈的过程，所涉及工艺参数众多，各工序之间互相影响且影响机理复杂。因此，仅通过冶金原理分析往往会得到很多无关特征和冗余特征，这增加了机器学习的时间和空间复杂度，严重影响了模型的预测准确性和运行效率，还会带来所谓的“维数灾难”[6]。由此可见，选择合适方法消除无关特征和冗余特征的影响，对于准确预测铸坯质量尤为重要。

数据挖掘任务中，面对高维情形下数据集中无关特征和冗余特征的影响，一般通过特征融合或特征选择来对特征集进行降维。特征选择主要是通过挖掘特征与类别间的内在联系，保留最有利于分类的有效特征和去除与类别无关的特征来实现降维[7]。主成分分析(PCA)是一种特征的主成分提取方法，该方法通过计算样本协方差矩阵的特征矢量，将输入空间的特征线性映射到低维特征空间中[8]。

鉴于现有方法局限性，本文根据某钢铁企业连铸生产过程中的参数构建数据集，提出了一种基于最大信息系数和主成分分析的两阶段特征降维方法，应用该方法对模型输入特征进行处理，并利用随机森林算法对模型的分类准确率进行验证，以期为后续提高铸坯质量缺陷预测模型的准确率提供依据。

1 两阶段特征降维方法

本文对基于冶金原理得到的特征集进行两阶段降维处理，方法框图如图1所示。由图1可知，第一阶段主要是消除无关特征影响，即相关性分析阶段。基于特征与铸坯质量缺陷之间的相关性进行特征选择，利用最大信息系数(maximum information coefficient，MIC)度量各维特征与铸坯质量缺陷的相关性，根据相关性大小对特征进行排序，删除相关性较弱的特征，得到的特征子集作为第二阶段的输入。第二阶段是消除冗余特征影响，即冗余性分析阶段。基于主成分分析(PCA)方法，将第一阶段得到的特征变换作为线性独立的各主成分，根据前k个主成分的累计方差贡献率，选择合适的主成分数量。

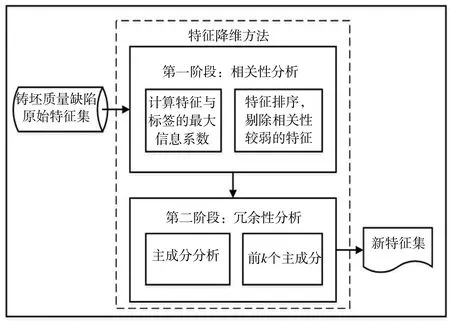
图1 两阶段特征降维方法框图Fig.1 Block diagram of two-stage feature dimensionality reduction method

1.1 第一阶段：特征选择

1.1.1 特征选择方法分析

常见的特征选择方法大致分为过滤法、包装法和嵌入法三类[6]。包装法与机器学习相结合，需要多次训练模型，有时间复杂度高等问题；嵌入法则将特征选择与机器学习算法训练放在同一过程中进行，所以必须要考虑特定模型算法是否适用于特定问题；过滤法不依赖于特定的机器学习方法，具有运行效率高的特点，适用于解决高维数据中的特征选择问题[9]，故本文使用过滤法进行特征选择。

过滤法中特征与标签之间的相关性越强，特征对标签的分类能力就越强，亦即该特征越重要，所以关键在于找到合适的指标来度量特征与标签间的相关性。常用的一些统计学指标如pearson系数、最小二乘回归误差等只能用来度量线性关系，但考虑到炼钢过程的复杂性，铸坯质量与各影响因素之间存在不确定性，即往往是非线性关系，故上述指标并不适用。虽然基于距离的度量指标ReliefF[10]和基于信息论的度量指标信息增益(IG)[11]能用于度量线性和非线性关系，但其无法有效衡量变量间的非函数依赖关系。

考虑到上述算法的局限性，本文使用最大信息系数来度量各特征与夹杂类缺陷的相关性，并根据相关性大小进行排序，来选择期望维数。最大信息系数不仅可以对大量数据中变量间的线性与非线性关系进行度量，而且还能广泛地挖掘出变量间的非函数依赖关系[12]。

1.1.2 最大信息系数

最大信息系数利用互信息和网格划分方法进行计算，对于任意特征X={xi,i=1,2,…,n}和标签Y={yi,i=1,2,…,n},n表示数据集样本个数，互信息定义为：

(1)

式中：p(x,y)表示特征X、标签Y的联合概率分布函数，p(x)、p(y)分别是特征X、标签Y的边缘概率分布函数。

定义D={X,Y}，将特征X、标签Y的值域分别划分为a、b部分，定义G为a×b的网格，可知网格G有多种形式，在每种网格形式内部计算互信息值，取最大值作为网格G的互信息值，记为MI(D,a,b)。改变a、b值，可得D在不同划分下的MI值，并进行归一化处理，取最大值作为D的最大信息系数，定义为：

(2)

式中：ab≤B(n)，B(n)为网格a×b的上限值，一般取B(n)=n0.6。

1.2 第二阶段：主成分分析降维

主成分分析(PCA)方法的步骤如下：

步骤1原始数据标准化，消除量纲影响。假设有n个样本m个特征的数据集，对于第i个样本的第j个特征xij有：

(3)

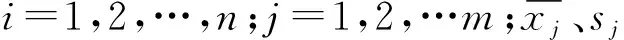
步骤2计算样本矩阵的协方差矩阵，并算得其特征值和特征向量，即：

(4)

式中：X*为标准后的数据矩阵。求得协方差矩阵C的特征值λ1≥λ2≥…≥λm及相应的特征向量(μ1，μ2，…，μm)。

步骤3确定主成分个数。前k个较大的特征值λ1≥λ2≥…≥λk代表前k个主成分的方差，前k个主成分的累计方差贡献率为：

(5)

若η(k)超过90%，则认为前k个主成分特征可反映原来高维特征的信息。

步骤4计算主成分。k个主成分对应的特征向量U=[μ1，μ2，…，μk]，由此得到特征的主成分矩阵，压缩后的特征数据为：

(6)

2 特征集构造

本文收集了某钢铁企业第三炼钢厂1月～5月的生产数据，经整理共获得数据131 676条，包含42项纪录，其中41项为工艺参数、设备参数、生产记录等(见表1)，剩下1项是铸坯质量缺陷细分类记录，该记录共含4669条数据。工厂将铸坯质量缺陷细分为22种，经统计可知，夹杂类质量缺陷占比为63.35%，高于其他类质量缺陷的总和，故本文以铸坯夹杂类缺陷为研究对象。

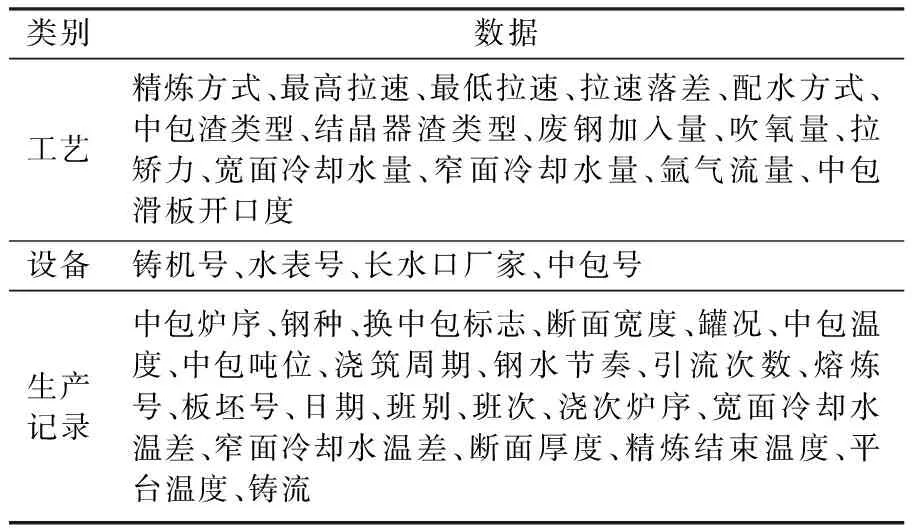
表1 铸坯生产过程参数Table 1 Process parameters of billet production

首先，剔除与铸坯夹杂类质量缺陷明显无关的记录(如熔炼号、日期等)。基于对夹杂类质量缺陷成因的相关研究[13-14]并结合炼钢厂的实际生产经验，最终确定夹杂类质量缺陷的22个影响因素，构成质量预测特征集，见表2。铸坯产生夹杂类质量问题仅有2958条数据，为保证样本均衡性，采取下采样策略，即在正常铸坯数据中随机抽取2958条，与前者组成了一个含5916个样本的数据集。数据集的前22列代表22个特征，最后一列代表标签，标签有两种值，分别为“正常”和“夹杂”。

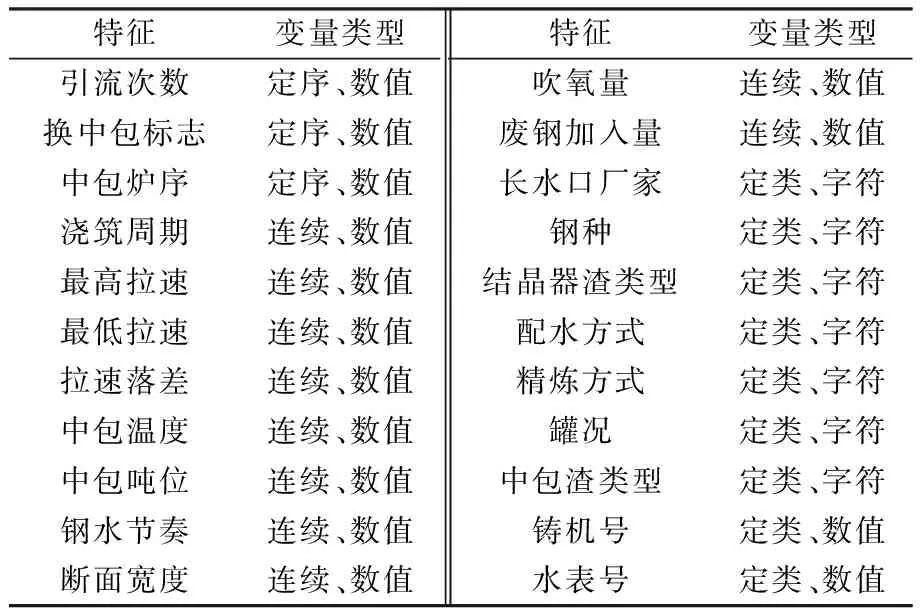
表2 铸坯夹杂类质量缺陷预测特征集Table 2 Feature set for predicting inclusion-related quality defects of billet

该组数据主要存在的问题是存在缺失值。对于连续型变量的缺失，采用均值填补；对于钢种、配水方式等定类变量的缺失，使用众数填补；对字符型变量进行数值化编码。另外，为了消除数据量纲影响以及提高算法的运行效率，特对数据进行标准化处理。

3 结果与分析

3.1 特征选择方法比较

通常使用分类器的准确率来评价特征选择方法所选特征子集的好坏[15]。为了验证MIC算法在铸坯质量缺陷预测问题中的适用性，本文还利用RelieF、IG算法对特征集进行降维，应用随机森林分类器对降维后的数据集进行处理，将分类准确率作为特征子集选择的评价标准，所有数据均是通过10折交叉验证取均值后获得。采用这3种度量指标均可以得到每维特征与铸坯夹杂类质量缺陷的相关性，根据相关性大小对特征进行排序，得到基于3种算法的特征相关性排序结果如图2所示。

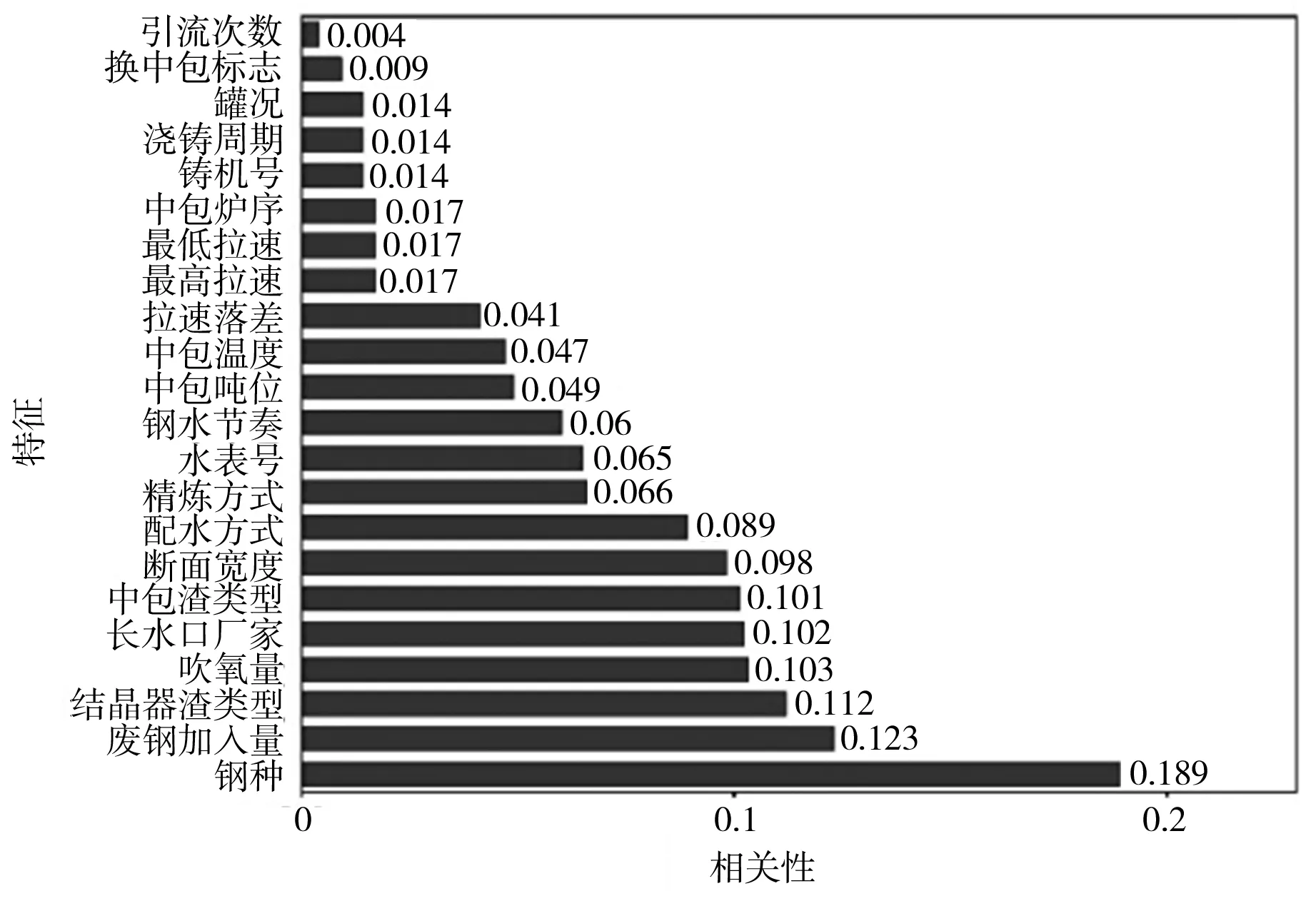
(a) MIC

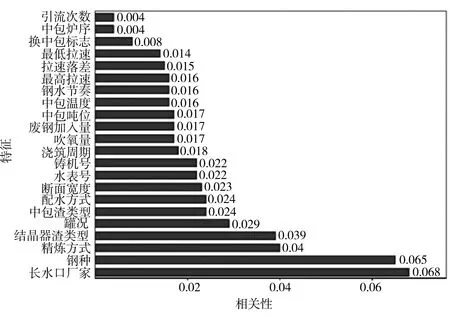
(b) ReliefF

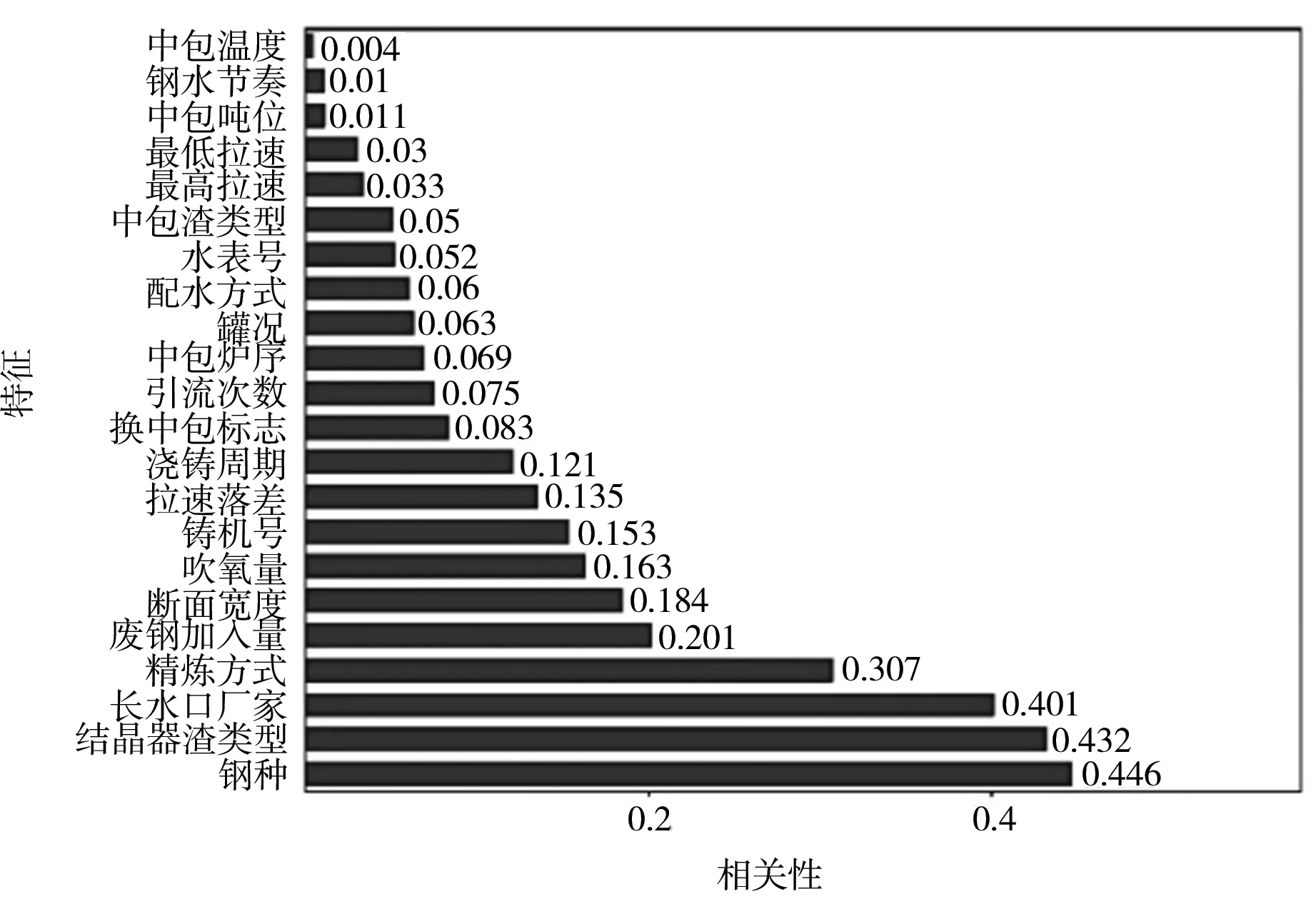
(c) IG图2 基于三种不同算法的特征排序Fig.2 Feature ordering based on different algorithms

应用随机森林分类器对3种度量指标进行评价时，依次删除相关性较小的特征，直至剩下一维特征为止，不同算法的分类准确率随删除特征数量(即数据集维度)的变化如图3所示。由图3可以看出，伴随着相关性较小特征的删除，3种算法的分类准确率与起点处相比均有所提升，而当相关性较高特征被删除时，模型的分类准确率则随之下降。

由图3还可见，采用MIC算法时，在删除8维特征时分类准确率最高可达89.0%，与未进行特征选择的情况相比，分类准确率提高了约4.2%；使用ReliefF算法，在删除4维特征时准确率最高为88.1%；使用IG算法，在删除5维特征时准确率最高为86.4%。综合来看，使用MIC度量指标进行特征选择，可以选出维度更低、分类准确率更高的特征，特征选择效果优于其他两类度量指标。

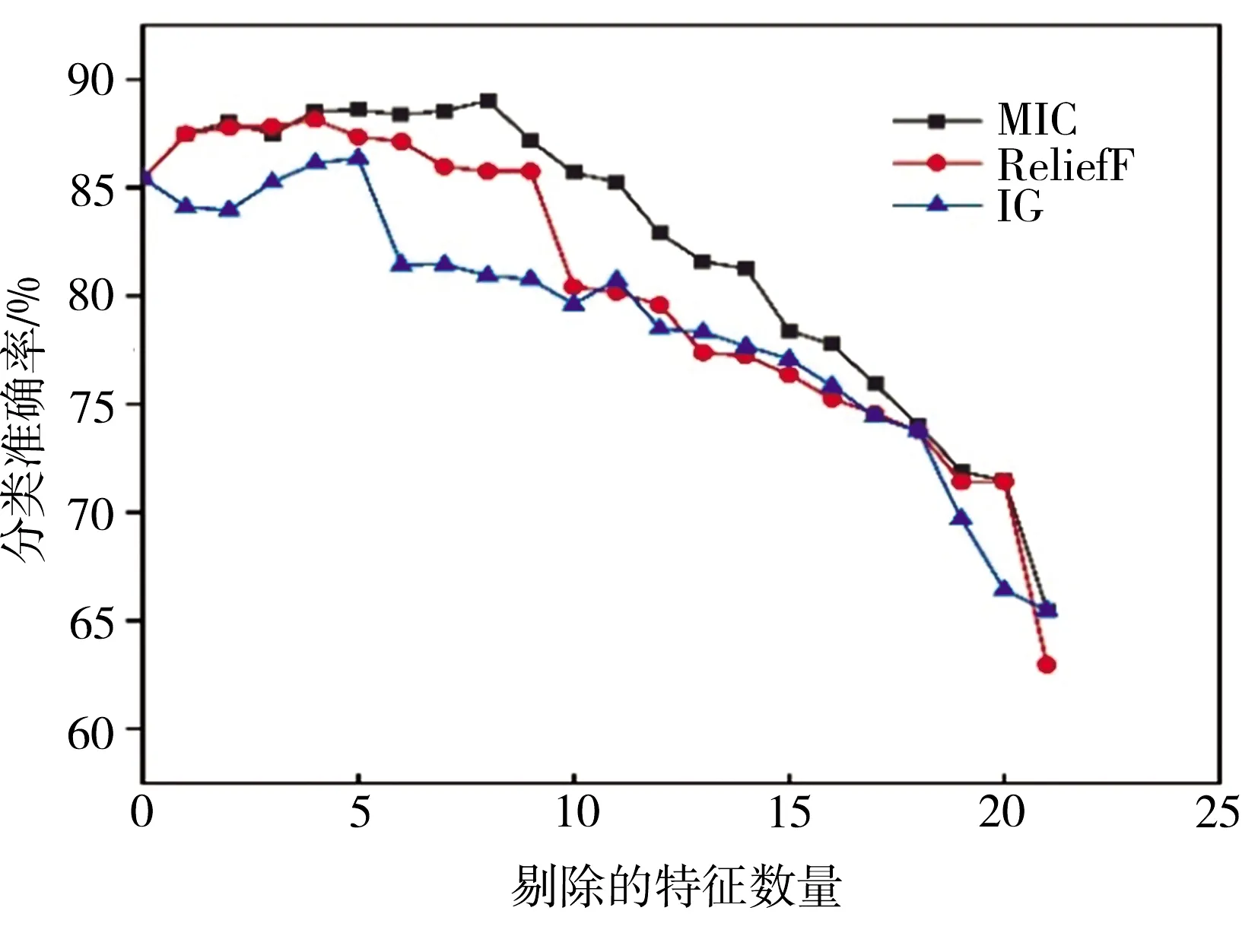
图3 三种算法于不同维度下的分类准确率Fig.3 Classification accuracies of three algorithms at different dimensionalities

因此，根据MIC算法的特征选择结果，删除相关性较小的8维特征后，保留与铸坯夹杂类质量缺陷相关的14个特征为：钢种、废钢加入量、结晶器渣类型、吹氧量、长水口厂家、中包渣类型、断面宽度、配水方式、精炼方式、水表号、钢水节奏、中包吨位、中包温度和拉速落差。

3.2 基于特征选择的主成分分析

为验证特征选择(MIC)结合主成分分析方法的有效性，分别对原始特征集和经特征选择后的特征集进行主成分分析，结果发现，前两个主成分的累计方差贡献率可达95%以上，后面的主成分对方差贡献率很小，所以确定将特征集降至两维，即原始特征集由5916×22(表示5916个样本、22个特征，下同)减小为5916×2，经特征选择后的特征集由5916×14降至5916×2。

图4所示为特征选择前后两类样本点的分布情况。由图4可见，经过特征选择后再降维，两类样本点更容易区分开。为进一步衡量主成分分析算法的降维效果，先将降维后数据进行归一化处理，然后用类内散布矩阵的迹表示类内距，用类间散布矩阵的迹表示类间距，降维后类间距与类内距的比值越大，表明降维效果越好，具体数值列于表3中。由表3可见，经过特征选择后再降维，类间距增大了0.0013，类内距减少了0.0089，两者比值增大了24.1%，由此可见，先对数据集进行特征选择(MIC)可以明显提升主成分分析算法的降维效果。

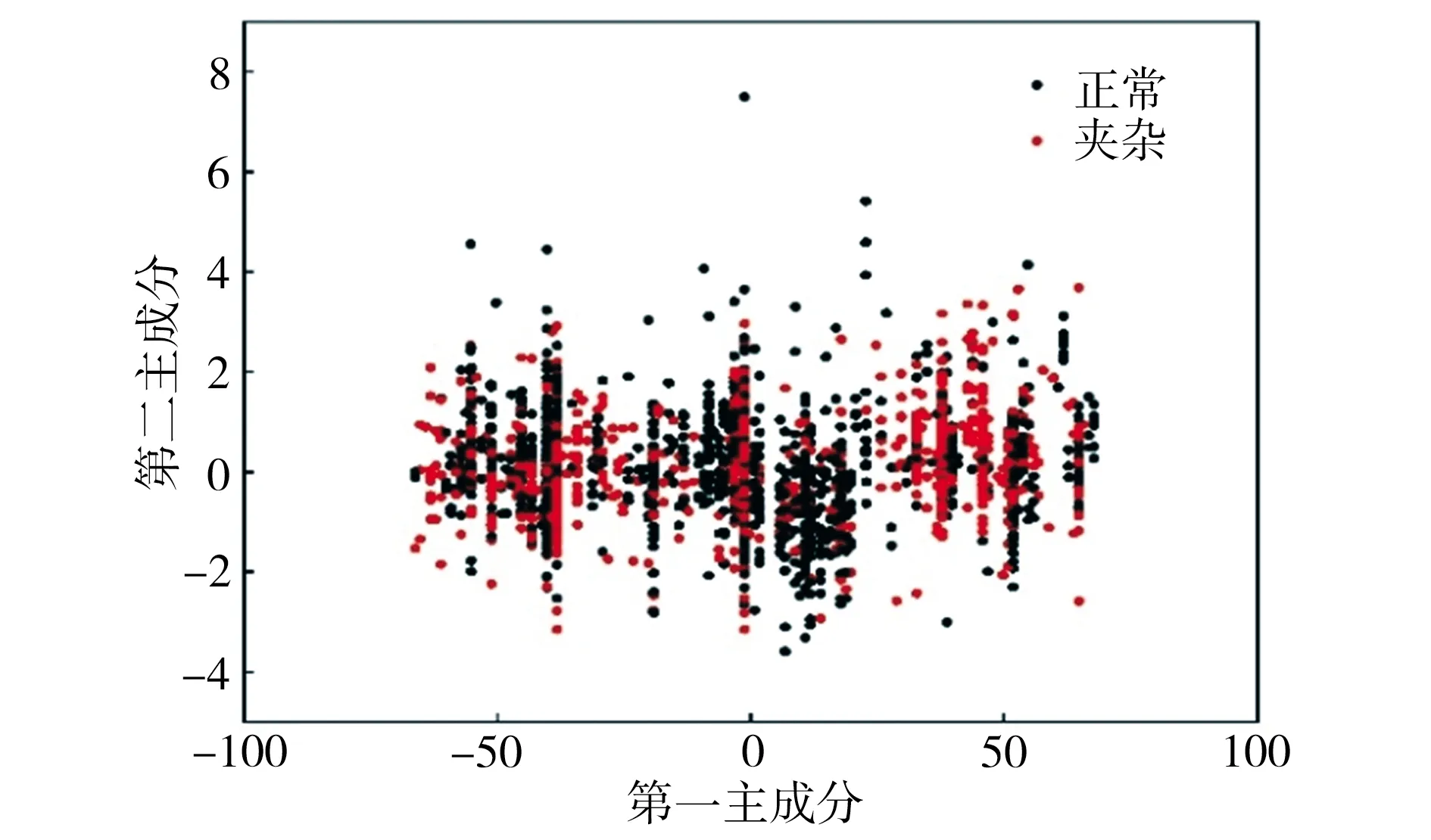
(a)未经特征选择

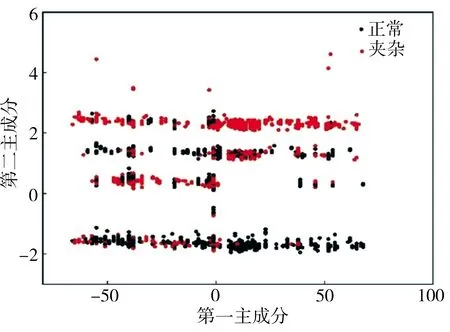
(b)经特征选择图4 特征选择前后基于PCA算法的降维效果Fig.4 Dimensionality reduction effects of PCA algorithm with and without feature selection

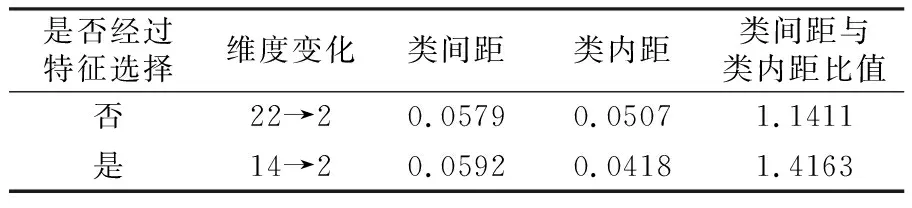
表3 基于PCA算法的降维效果比较Table 3 Comparison of dimensionality reduction effects based on PCA algorithm

3.3 效果验证

利用随机森林分类器对不同特征处理算法的分类精度进行评估，结果如表4所示，所有分类准确率均是通过10折交叉验证取均值后获得。由表4可见，与未处理的数据集相比，基于MIC、PCA及MIC+PCA的特征降维方法均能提高模型的分类准确率，其中两阶段降维算法比单独使用MIC和PCA算法的分类精度更高，相比于未处理数据集和单独使用MIC、PCA算法处理后的数据集，两阶段降维算法的分类准确率依次提高了8.1%、3.7%和5.2%，由此可见，本文提出的基于最大信息系数和主成分分析的两阶段特征降维方法，可以应用于铸坯夹杂类质量缺陷的预测模型。

表4 不同特征处理方法的分类准确率Table 4 Classification accuracies of different feature processing methods

4 结论

(1)与使用ReliefF、IG算法相比，使用最大信息系数(MIC)作为特征选择的度量标准，选出的特征维度更低，分类准确率提升明显。由此可见，在铸坯夹杂类质量缺陷预测问题中，使用MIC算法能较准确地度量各影响因素与铸坯夹杂类质量缺陷间的相关性。

(2)与单独使用(MIC)特征选择和单独使用主成分分析(PCA)算法相比，基于最大信息系数和主成分分析的两阶段特征降维方法可获得最佳的分类准确率，表明本文提出的两阶段降维方法有利于提高铸坯夹杂质量缺陷预测模型的预测精度。